基于黄金角度调制的空间调制MIMO 系统性能研究
杨芷华,黄丽美,汤小波
(五邑大学智能制造学部,江门529020)
0 引言
随着通信技术发展,高传输速率和高频谱利用率已成为下一代无线通信系统关键性能指标[1]。在现有通信技术中,多输入多输出(Multiple Input Multiple Output,MIMO)系统由于多天线系统配置,信号可通过多天线系统同时发送和接收,从而在不增加额外频谱资源负担和发信功率的情况下改善系统通信质量[2-5]。然而,由于多天线系统在相同频段同时发送独立数据流,致使传输信道间产生强烈的信道间干扰(Inter-Channel Interference,ICI),增加了MIMO 系统接收端正确译码的复杂度[6-9]。针对MIMO 系统存在的不足,空间调制(Spatial Modulation,SM)传输方案[10-12]能有效降低系统复杂度。空间调制传输方案在每个传输时隙仅激活一根发送天线,不仅利用传统调制符号传递信息,还利用发送调制符号的天线位置传递信息。
传统符号调制方式包括脉冲振幅调制(Pulse Amplitude Modulation,PAM)、矩形QAM、星型QAM[13]、相移键控调制(Phase Shift Keying,PSK)等。其中QAM 调制方式在无线通信系统中使用最为广泛。文献[14-15]基于花瓣、树叶等螺旋叶序植物提出了黄金角度调制方式(Golden Angle Modulation,GAM),实验表明:①在信噪比受限和星座点数相同时,GAM 调制方式互信息性能优于正方形QAM;②星座点数越大,GAM 调制方式的互信息越逼近香农信道容量。
鉴于GAM 调制方式在高传输速率时的互信息性能,为提高SM-MIMO 系统传输性能,本文研究了基于GAM 调制的SM-MIMO 系统的误码性能和互信息性能。
1 基于GAM调制的SM-MIMO通信系统
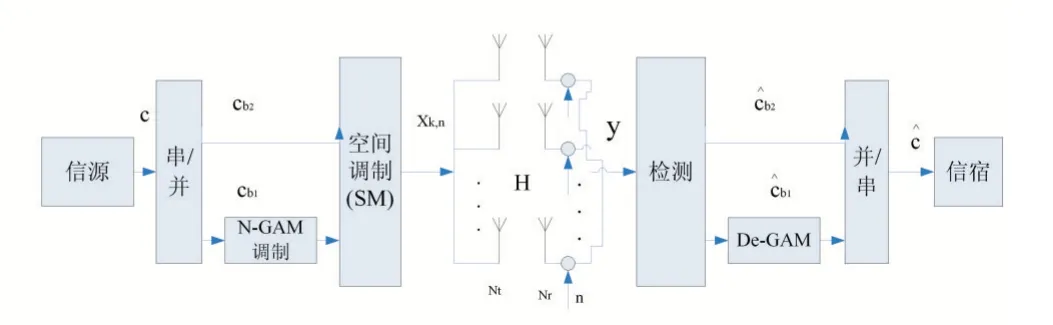
图1 基于GAM调制的SM-MIMO通信系统方框图
图1 所示为基于GAM 调制的SM-MIMO 通信系统方框图。MIMO 系统配置有Nt根发送天线和Nr根接收天线,构成Nr×Nt维信道矩阵H,H 中的元素hij(i=1,...,Nr,j=1,...,Nt)服从均值为0、方差为1 的复高斯分布。在每个传输时隙,发信端首先将信源产生的长度为b=log2(Nt∙M)二进制比特流c 串并转换成长度为b1=log2M 和长度为b2=log2Nt的比特流cb1和cb2两部分。对长度为b1=log2M 的比特流cb1按本文第三部分给出的 N-GAM 调制方式映射成调制符号sn(n=1,2,…,N)∈Q(Q 为N-GAM 调制星座);长度为b2=log2Nt的比特流cb2用于选取发送天线,将所选发送天线空间位置映射成第k 位为1 的Nt维单位向量ek(ek为Nt×Nt单位矩阵I 的第k 列,k=1,2,…,Nt);在每个传输时隙,sn与ek形成发送向量:

xk,n经传输信道H 到达接收端后,接收端接收信号为:

式(2)中n 为Nt×1 维 高 斯 噪 声,其 元 素ni(i ∈{1 ,2 ,…,Nt})是均值为0、方差的复高斯变量,即
接收端根据收到的y 和已知的信道状态信息H,按最大似然检测算法(Maximum Likelihood,ML)可检测出调制符号̂ 和天线序号
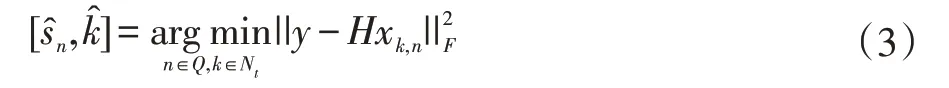
式(3)中||∙||F为Frobenius 范数。
2 黄金角度调制
在本文所设计的基于黄金角度调制的SM-MIMO系统中,考虑文献[15]中圆盘型GAM 情形。设GAM 星座图中每个星座点等概,即第n 个星座点调制概率pn=1/N,N 为GAM 星座点数目。则第n 点GAM 调制符号sn可表示为:

式(4)中,rn为第n 个星座点的半径,2πψ 为黄金角度弧度值,黄金比例
随着n 增大,设第n+1 个星座调制符号sn+1的半径rn+1>rn,sn+1的位置由坐标轴正半轴绕原点逆时针旋转(n+1)×2πψ 弧度(约(n+1)×137.5∘)确定。式(4)中半径rn可由式(5)计算得出:

式(5)中Pˉ为平均功率限制。
以图2 中给出的8 点GAM 星座图为例对GAM 调制方式进行说明。调制符号s1到s8对应自然二进制比特,即调制符号s1表示比特序列000,调制符号s2表示比特序列001,以此类推。s1在星座图中的位置由半径为r1的圆与坐标轴的正半轴绕圆点逆时针旋转137.5∘的交点确定,类似的,s2的位置由半径为r2的圆与坐标轴的正半轴绕圆点逆时针旋转275∘(2×137.5∘)的交点确定。图3 给出了不同星座点规模GAM 调制的星座图。

图2 8点GAM星座图

图3 GAM调制星座图
3 GA-SM系统互信息分析
按图1 所示,基于黄金角度调制的SM-MIMO 系统的信道输入变量X 为离散型随机变量,设X 服从均匀分布,则:

由于高斯噪声的存在,输出变量Y 为连续型随机变量,信道转移概率密度函数为:

由式(6)和(7)可得:

由贝叶斯公式知有式(9)成立:

根据文献[16],GA-SM 系统互信息可表示为:

式(10)中E[∙]表示求统计平均。
4 仿真实验
按图1 所设计的基于黄金角度调制的空间调制MIMO 系统,本节对不同系统配置条件下的误码性能和互信息性能进行了实验仿真。
4.1 误码率
图4 所示为基于黄金角度调制的SM-MIMO 系统误码性能仿真曲线图,Nt=2,Nr=2。从仿真曲线可知,在大信噪比时,当BER=10-4时,基于GAM 调制的SM-MIMO 系统性能相比于基于QAM 调制的SM-MIMO 系统误码性能约有0.7dB 的增益。

图4 GA-SM-MIMO系统误码曲线图
图5 所示为基于黄金角度调制的SM-MIMO 系统误码性能仿真曲线图,Nt=4,Nr=4。由仿真曲线可知,当BER=10-4时,基于GAM 调制的SM-MIMO 系统性能相比于基于QAM 调制的SM-MIMO 系统误码性能约有0.4dB 的增益。
4.2 互信息
图6 所示为QAM 与GAM 在SM-MIMO 系统的互信息仿真曲线图,Nt=4,Nr=4。从仿真曲线可知,随着信噪比的增大,基于GAM 的SM-MIMO 系统的互信息相比于基于QAM 的SM-MIMO 系统的互信息更接近香农限。
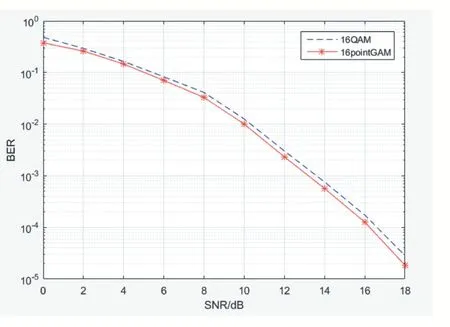
图5 GA-SM-MIMO系统误码曲线图
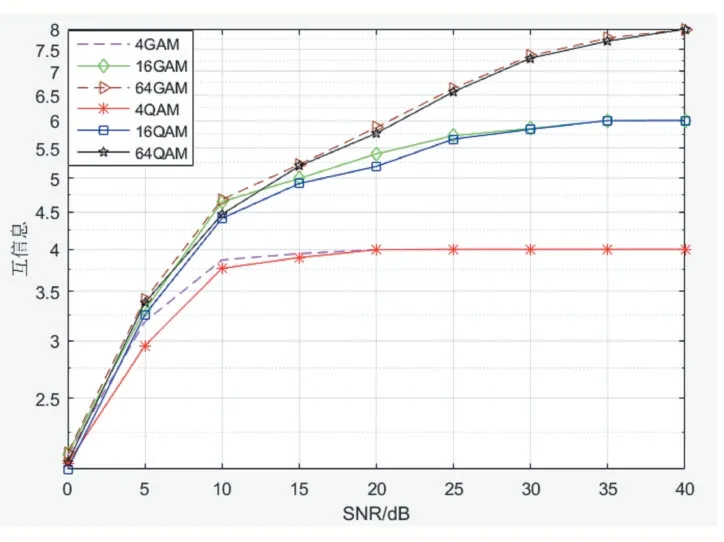
图6 QAM与GAM在SM-MIMO系统的互信息曲线图
5 结语
本文在2 发2 收的SM-MIMO 系统和4 发4 收的SM-MIMO 系统中采用了一种新颖的调制方式——GAM 调制,并与传统的QAM 调制进行了误码性能和互信息性能的仿真实验对比。实验结果表明:在SMMIMO 系统天线配置相同时,基于GAM 的SM-MIMO系统相比于基于QAM 的SM-MIMO 系统具有更优异的误码性能,且互信息也更趋近于香农限。

