常数度的结构化P2P 系统Cycloid 研究
徐丽新
(广东工程职业技术学院信息工程学院,广州510520)
0 引言
早期的基于DHT(分布式哈希表)的结构化P2P系统模型典型的有Chord[1]、Pastry[2]、Tapestry[3],其路由表大小和网络直径均为O(logN),而系统模型CAN[4]是O(d)和O(d*N1/d)。这些模型在大量节点的加入和离开网络搅动剧烈时会产生巨大的开销[5],为了减少开销,一些具有常数度(即节点只维护常数个邻居)的P2P 系统被提出来如Cycloid[8-9]、Koorde[7]和Viceroy[6]等。这些系统具有O(logN)的网络直径,固定地维护较少的常数个邻居,如Cycloid 和Viceroy 邻居数均为7、Koorde 邻居数最小为2。本文详细介绍了Cycloid系统。
1 Cycloid的拓扑结构
Cycloid 的网络拓扑结构是基于立方体连接环(CCC:Cube-Connected Cycle)图。在Cycloid 系统中,最多可容纳n=d*2d个节点,每个节点维护O(1)个邻居节点,每个查询要经过O(d)跳路由转发。Cycloid 系统不必是完全的,它可以有少于d*2d个节点。
一个d 维的立方体的每个顶点用d 个节点组成的环来代替就得到一个d 维的CCC 图。它包含d*2d个度为3 的节点。每个节点用一对索引值(k,ad-1ad-2...a0)表示,其中k 是环索引,ad-1ad-2...a0是立方体索引。环索引是一个介于0 和d-1 之间的整数,立方体索引是一个介于0 和2d-1 之间的二进制整数。如图1。

图1 三维CCC图
2 相关术语
局部环(local cycle):具有相同立方体索引值的节点根据k 值排序组成的循环。
远环(remote cycle):远环是指不同立方体索引值的局部环。
主节点(primary node):在局部环中环索引值最大的节点为这个环的主节点。
大环(large cycle):根据立方体索引值排序的局部环组成的循环。
前导节点(predecessor):在一个局部环中,逆时针方向遇到的第一个节点[10]。
后继节点(successor):在一个局部环中,顺时针方向遇到的第一个节点[11]。
前导远环(preceding remote cycle):在大环中,逆时针方向遇到的第一个局部环。
后继远环(succeeding remote cycle):在大环中,顺时针方向遇到的第一个局部环。
3 关键字的分配
Cycloid 的DHT 使用一致性哈西函数在ID 空间上分配关键字,节点的ID 和关键字被一致的分布在一个d*2d的ID 空间中。关键字的分配和Pastry 很相似,只是Cycloid 的每个节点与一对环索引和立方体索引相关联。对某个关键字,它要映射的节点的环索引被设置为它的哈西值模d,立方体索引被设置为它的哈西值除以d。如果Cycloid 的节点组成一个完整的CCC 图,一致性哈西函数将把关键字k 映射到节点k。如果一个关键字的ID(k,ad-1ad-2...a0)不是一个活动节点,这个关键字会被分配到先是数字上最接近ad-1ad-2...a0,然后数字上最接近k 的节点上。例如,在(2,1101)和(2,1001)中,(1,1101)更接近(2,1101)。当两个节点到关键字ID 的距离相同时,关键字的后继节点将负责存储这个关键字[12]。
4 路由表结构
在Cycloid 系统中,每个节点为了与系统的其余部分连接要维护一个有7 个入口的路由表。图2 是一个8 维Cycloid 系统中节点(4,101-1-1010)的路由表。
一般情况下,节点(k,ad-1ad-2…a0)(k ≠0)有7 个邻居节点。其中一个立方体邻居(k-1,ad-1ad-2…akxx…x)(x任取0和1),两个循环邻居(k-1,bd-1bd-2…bo)和(k-1,cd-1cd-2…c0)是环索引为k-1 mod d、立方体索引为第一个大于和小于ad-1ad-2...a0且最大不相同位的下标值小于k 的节点。即:
(k-1,bd-1bd-2…b1b0)=min{∀(k-1,yd-1yd-2…y1y0)|yd-1…y0≥ad-1…a1a0}
(k-1,cd-1cd-2…c1c0)=min{∀(k-1,yd-1yd-2…y1y0)|yd-1…y0≤ad-1…a1a0}
环索引k=0 的节点没有立方体邻居和环邻居。立方体索引为0 的节点没有小的环邻居,立方体索引为2d-1 的节点没有大的环邻居。在局部环中,左内叶子集结点(left inside leaf set node)指向当前节点的前导节点[13],右内叶子集节点(right inside leaf set node)指向当前节点的后继节点[14]。在大环中,左外叶子集结点(left outside leaf set node)指向当前节点的前导远环的主节点,右外叶子集结点(right outside leaf set node)指向当前节点后继远环的主节点。换句话说,局部环将具有相同立方体索引的节点连接在一起,而大环连接了所有立方体索引不同的节点。一个环上的节点可以直接或间接地到达其他环上的节点。容易看出,如果所有的节点都是活动的那么网络就是传统的立方体连接环(CCC)。
5 路由算法
Cycloid 的路由算法模拟了CCC 的路由算法从源点(k,ad-1ad-2...a0)到目标点(l,bd-1bd-2...b0),即使缺少许多节点,其余的节点仍然能够被连接在一起,所以我们的链接模型是弹性的。路由过程如图3。
Cycloid 的路由算法分为三个阶段(N 表示当前节点和目标节点的最大的不同位下标):
(1)上升阶段:当关键字k≤N 时,将该请求沿外叶子节点转发直到环索引k≥N。
(2)下降阶段:当k=N 时,将请求转发到立方体邻居;否则,为了靠近目标立方体索引,需将请求转发到内叶子节点和环邻居中最接近目标的节点。
(3)横向阶段:当目标id 在叶子集中,将请求转发到最近叶子节点,直到最接近的节点就是当前节点本身。
特别的,上升阶段从外叶子集中选择立方体索引数字上最靠近目标的节点。在下降阶段,当k>N 时,选择立方体索引最靠近目标的节点。当k<N 时,从环邻居和内叶子集中选择更接近目标的环邻居。当k=N时,前缀路由算法从左到右的将ad-1…a1a0改变为bd-1…b1b0。沿着立方体链,信息被送到与关键字至少匹配更多一位前缀的节点。立方体链、环链或内叶子集是可以交替使用的。在横向阶段,如果目标在局部环中,信息将被送到内叶子集中的一个节点;否则,信息将被转发到外叶子集中数字上更靠近目标的节点。如果最近的节点是它自己,那么就到达了目标,搜索就完成了。在整个查询过程中,如果某个节点不能找到或是已经失效,那么将选择叶子集中数字上更靠近目标的节点。叶子集在路由算法中起的作用很大,它用来改进路由的效率,检查查询的终止条件,并包围关键字空间以防止超过目标。
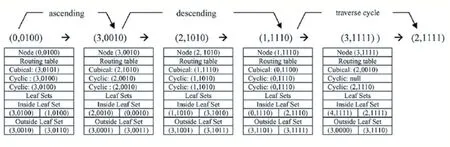
图4 Cycloid路由实例
图4 是一个4 维Cycloid 路由的实例,一个请求从节点(0,0100)路由到(2,1111)。节点(0,0100)与目标的最大不同位下标MSDB 是3。由于(0,0100)的环索引k=0 小于N,所以它处于上升阶段,选择外叶子集中的节点(3,0010)。(3,0010)的环索引k=3 等于N,所以处于下降阶段,请求被转发到它的立方体邻居(2,1010)。(2,1010)的环索引k=2 等于它的MSDB,将请求转发到它的立方体邻居(1,1110)。因为目标(2,1111)的立方体索引1111 在(1,1110)的叶子集中,所以将请求转发到(3,1111)。与此相似,(3,1111)发现目标在他的叶子集中,就将请求转发到(2,1111),请求就到达了目的地。
路由过程三阶段中的每一个的界都是O(d)跳,所以整个路径的长度是O(d)。算法背后的思想是保持距离不断的减小。文献[4]用算法的收敛性和可达性证明了路由算法的正确。所谓收敛性是指路由的每一步都减少了到目标的距离。所谓正确性是指每个相继的节点都把信息转发到下一个节点。因为每一步都是将查询请求转发到与关键字共享更长前缀的节点或共享相同前缀但数字上更接近目标的节点,所以路由算法是收敛的。这个路由算法可以很容易的扩充以增加容错性。当立方体链或环链为空或失效时,可以将信息转发到叶子集中的节点。以上讨论的是基于7 个入口的Cycloid,它可以被扩展到在内外叶子集中包括两个前导和连个后继节点。模拟显示11 个入口的Cycloid具有更好的性能。
6 自组织
P2P 系统的高动态性意味着节点会经常地加入或离开网络。Cycloid 用分布式的算法处理节点的加入和离开,不需要知道整个网络的信息。
6.1 节点加入
当一个新节点加入时,首先用第3 节的方法得到自己的ID。然后,它初始化自己的路由表和叶子集[15],并通知其他节点。像Chord 一样,Cycloid 假设任何新节点都知道一个活动节点。假设已知的活动节点是A=(k,ad-1ad-2...a0),新节点是X=(l,bd-1bd-2...b0)。根据第5 节讨论的路由算法,节点A 将把加入信息路由到其ID 在数字上最靠近X 的节点Z 上。Z 的叶子集将是X的叶子集的基础。特别的,需要考虑下面两种情况:
(1)如果X 和Z 在同一个环中,那么Z 的外叶子集将成为X 的外叶子集。X 的内叶子集将根据Z 的内叶子集进行初始化。如果Z 是X 的后继节点,Z 的前导和Z 是X 的内叶子集中相应的左节点和右节点。否则,Z 和Z 的后继是左节点和右节点。
(2)如果X 是它的局部环中的唯一节点,那么Z 和X 不在同一个环中。在这种情况下,X 的内叶子集中的两个节点就是X 本身。X 的外叶子集根据Z 的外叶子集初始化。如果Z 的环是X 的后继远环,那么Z 的左外叶子集节点和Z 所在环的主节点就是X 的外叶子节点中的左右节点。否则,Z 所在环的主节点和Z 的右外叶子节点是X 的外叶子集的左右节点。
节点加入系统之后,需要通知它的内叶子集中的节点。如果他是局部环的主节点,则还要通知它的外叶子集中的节点。当内叶子集中的节点收到加入信息时,它们会更新自己的路由表。当外叶子集节点收到加入信息时,除了更新自己的路由表之外,它们还要将此信息传播到它的内叶子集节点[16]。如此,加入信息沿着加入节点的邻居远环传播,直到所有的环都完成更新。
6.2 节点离开
在一个节点离开之前,它需要通知它的内叶子集节点[17]。在Cycloid 中,一个节点只有出的连接而没有入的连接。因此,将要离开的节点不能通知那些将它作为立方体邻居或环邻居的节点。如果该节点是局部环中的主节点,则还需要通知外叶子集中的节点。当内外叶子集节点收到节点的离开信息时都需要更新自己。而外叶子集节点还需要一个一个的通知它们的局部环中的其他节点,这个过程最多需要d 步。只有那些将这个要离开的节点作为内叶子或外叶子的节点被更新。那些将这个离开节点作为立方体邻居或环邻居的节点不能被更新。
7 结语
CCC 图的特性保证无论维数取多少,节点的度都保持为3,这成为Cycloid 的节点保持常数个邻居的基础。同样的具有常数度的P2P 系统中Viceroy 使用butterfly 图,Koorde 使用de bruijn 图。模拟结果[6]显示Cycloid 适合大规模的高动态的环境,具有更好的平均定位效率,在稀疏网络情况下,具有更均匀的关键字分布和负载平衡性能。今后我们要进一步研究更多的P2P 系统和互连网络,寻找更好的适合P2P 的网络拓扑结构。

