粗糙集理论在地下工程风险管理中的应用

沈雪平 袁艺博

（河南理工大学土木工程学院 河南焦作 454150）

1 引言

城市地下工程建设的快速崛起，缓和了我国城市建设用地紧张的局面，同时也提高了我国城市基础设施建设的工业化水平和充分响应了国家要建设智能、集约、绿色和环保建筑的号召，但是在快速发展的背后却也面临着一些问题。因为地下工程赋存于施工环境更加复杂的地下，相对于在地面施工作业，地下作业更容易诱发风险因子，从而导致风险事故的发生。这不仅对国民经济造成严重影响，更是对实现人民幸福中国梦愿望的一种背离。因为我国对地下工程的开发相对于国外晚了几十年，所以对地下工程风险管理研究还处在初步探索阶段，主要都集中在对地下工程风险前期的识别阶段，而对地下工程风险评估却处于相对贫乏的时期，本文提出了基于粗糙集理论的地下工程风险的评估研究。

2 地下工程现状与风险管理

2.1 地下工程的简述

钱七虎院士曾说，21世纪，为了节约能耗、保护环境，人类必须大量的利用地下空间，因此，21世纪对人类来说是“地下空间”的世纪[1]。我国是一个地大物博加人口众多的国家，虽然国土面积位列世界第三，但是和人口众多比起来无异于是杯水车薪。要想解决建设用地紧张的问题，大力发展地下空间是个不错的选择，除了国家相继发布一些政策以推进地下空间的开发利用如《城市地下空间开发利用管理规定》，地方政府也加快推进城市地下空间开发的脚步，如《福建省人民政府关于加快城市地下空间开发利用的若干意见》、《杭州市区地下空间建设用地管理和土地登记暂行规定》等，这无不彰显着中国已经进入城市地下空间开发利用的繁荣时期。

2.2 风险管理的重要性

然而地下工程与其他建筑工程相比，因为要在风险因子较多的地下环境中作业，施工工作面相对狭窄不像地面上作业那么宽敞而且周围环境相对较差，所以稍有不慎就可能发生危险。2008年 11月15日下午，杭州地铁湘湖站“北2基坑”发生坍塌，造成死亡21人、重伤1人、轻伤3人，直接经济损失达4962万余元。这些触目惊心的数字使我们深刻的认识到对城市地下工程进行风险管理势在必行。风险管理作为项目管理九大要素之一，也越来越被赋予着重要的的“使命”。风险并不可怕，可怕的是风险来临时我们还没有意识到。工程项目的风险评价的方法有多种，但无外乎为定性和定量这两种方法。定性方法主观性大，而定量方法比较客观。无论采用哪种方法，基本上离不开评价指标体系的构建和其权重的确定。

3 粗糙集理论

粗集理论是由波兰华沙理工大学Z.Pawlak教授于20世纪80年代初提出的一种研究不完整、不确定知识和数据的表达、学习、归纳的理论方法[1]。粗糙集理论作为一种处理不确定性问题的数学数据挖掘工具。其主要思想是在保持分类能力不变的前提下，通过知识约简，导出问题的决策或分类规则。目前，粗糙集理论已被成功的应用于机器学习、决策分析、过程控制、模式识别与数据挖掘等领域[2]。

3.1 知识和知识库

粗糙集理论的研究对象是知识和数据，这里的知识和我们传统认知的知识有出入。K=（U，R）是一个知识库，其中U≠Ø是我们感兴趣的对象组成的有限集合，称为论域。U的任何子集X，称为U中的一个概念或范畴。U中的任何概念称为关于U的抽象知识，简称知识。通俗来说就是对我们感兴趣的对象组成的集合进行划分的依据或者能力。而R是U上的一个等价关系。

3.2 上下近似关系

当论域中的子集X不能在知识库K中用R来精确定义时，就称为X为这个知识库中的粗糙集。那我们怎么来表示这些粗糙集呢，我们可以用和来表示，是由那些根据知识R判断肯定属于X的U中元素组成的集合，是那些根据知识R判断可能属于X的U中元素组成的集合。Ind(R)称为R上的不可区分关系或者是不可分辨关系，U/ind(R)显然构成了论域U上的划分，经常简写为U/R。

3.3 知识约简

所谓知识约简，就是去掉对知识库分类能力不会产生影响的多余属性，知识约简一直是粗糙集理论的核心问题，用下式子可以简明表示：令R为一族等价关系，i∈R，如果ind(R)=ind(R-i),则称i为R中不必要的；否则称i为R中必要的。

从这里可以看出知识约简可以用来消除知识库的冗余，另外我们可以借助知识约简这种思想对属性进行重要度的排序[3]。

4 粗集理论在风险管理中的应用

随着时代的发展和技术的进步，地下工程施工建设中的机械化程度越来越高，逐渐形成了以明挖现浇、盾构法、顶管法、浅埋暗挖法为主的施工方法。纵观地下工程施工建设的发展，明挖法在其他新的工法发展的强势冲击下还是占主流趋势，本文以粗糙集理论为基础，建立关于明挖法地下工程施工风险事件的知识表达系统，应用知识约简相关思想和属性重要度的概念，以此来得到风险评价指标的权重集。

4.1 风险知识表达系统的构建

粗糙集理论本身是一种数据挖掘的工具，要想建立粗糙集的知识表达系统，就必须收集相关的数据，才能建立相关的知识库。通过大量查阅文献包括书籍、期刊论文和学报，以及在国家相关网站搜索例如国家安全生产监督管理总局统计各类风险事故，还有搜索相关的新闻网站。共搜索到100起明挖法发生的施工安全事故[4-10]，并总结出各种风险事故发生原因。

表1 明挖法重大安全事故案例表

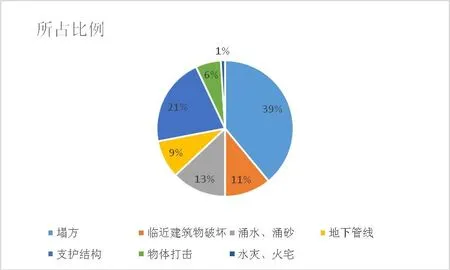
通过对施工安全事故资料数据的分析可以得出地下工程风险事故主要有塌方、涌水涌砂、地表塌陷、支撑破坏、周围建筑物破坏、地下管线破坏、水、火宅等类型。

知识表达系统一般的表达式为S=（U,R,V,f）这样的四元组形式，其中前面已经说过U为论域，是我们要研究的对象的集合，既然是要分析的对象不能为空集；R为研究对象的特征的非空有限集合；V为属性集合对应的值域，例如Vb是属性b对应的值域；f就是一个映射函数，例如属性集合为自变量，把属性集合里面的数在V中找到对应的函数。通过收集相关的资料和数据以及采取对相关方面的专家询问相结合的方式建立风险知识表达系统。知识表达系统常以数据表格的形式表达，粗糙集的关系表分为信息表和决策表两种类型，只有具备条件属性和决策属性的知识表达系统才称为决策表。施工风险知识表达系统没有决策属性只有条件属性，以明挖法下的施工风险因素为研究对象，称为明挖隧道施工风险的对象论域U,以各种明挖法下风险事故发生为条件属性，通过风险因素能不能直接导致风险事故的发生对而论域中的对象进行赋值，例如，如果项目人员这个风险因素不能直接导致塌方这个风险事故的发生，那么两者交叉的表格里就会赋值为0，以此类推，建立下面的信息表。

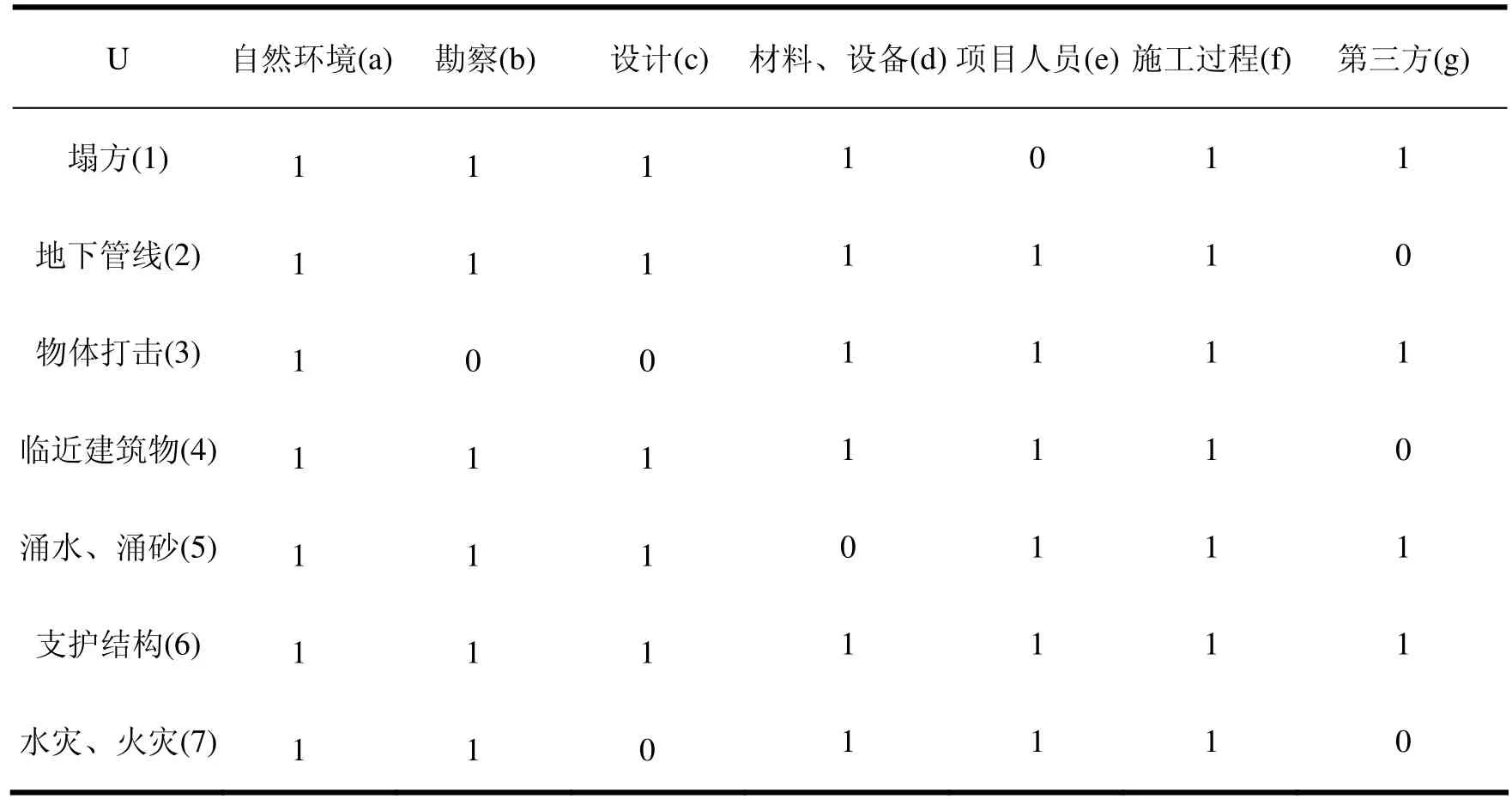
表2 关于风险事故的知识表达系统

在信息表中，不同的影响因素相对于评价指标可能具有不同的影响程度，例如，当购房者想要买住宅时，在房子的朝向、层高、价格和面积等因素中，购房者更倾向于价格为首要考虑的因素。为了找出某些因素相对于整个评价体系的重要性，拟采取去掉某一个因素和之前有该因素前后两者对论域中研究对象分类的影响，若去掉该因素之后，对论域中研究对象分类变化较大，则说明该因素的影响大，即应重点考虑，反之则反。

如何通过属性把论域中对象进行划分，是粗糙集理论的研究核心，本文通过沿用粒度的相关来表达属性的重要度[11]，设R的划分为U/R={U1，U2，……Un}，则相关研究对象的知识粒度表达式为|R|=

4.2 属性权重的计算

设 A={a，b，c，d，e，f，g}，A1={b，c，d，e，f，g}，A2={a，c，d，e，f，g}，A3={a，b，d，e，f，g}，A4={a，b，c，e，f，g}，A5={a，b，c，d，f，g}，A6={a，b，c，d，e，g}，A7={a，b，c，d，e，f}，U/ind(a，b，c，d，e，f，g)={{1}，{2}，{3}，{4}，{5}，{6}，{7}}；去掉属性 a 以后，U/indA1={{1}，{2，4}，{3}，{5}，{6}，{7}}。由上面的公式可得|A|=12+12+12+12+12+12+12=7，|A1|=12+22+12+12+12+12=9，则A1/A=9/7=1.286，同理可得：U/indA2={{1}，{2}，{3}，{4}，{5}，{6}，{7}}，|A2|=12+12+12+12+12+12+12=7，A2/A=7/7=1； U /indA3={{1，5}，{2，7}，{3}，{4}，{6}}，|A3|=22+22+12+12+12=10，A3/A=10/7=1.429；

U/indA4={{1}，{2}，{4}，{3}，{5}，{6}，{7}}，|A4|=12+12+12+12+12+12+12=7，A4/A=7/7=1；

U/indA5={{1,6}，{2}，{4}，{3}，{5}，{7}}，|A5|=12+22+12+12+12+12=9，A5/A=9/7=1.286；

U/indA6={{1}，{2，6}，{3}，{5}，{4}，{7}}，|A6|=12+22+12+12+12+12=9，A6/A=9/71.286； U/indA7={{1}，{2}，{4}，{3}，{5}，{6}，{7}}，|A7|=12+12+12+12+12+12+12=7，A7/A=7/7=1；

各属性的权重计算如下：

自然环境：P(a)=9/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=9/58=0.155；

勘察：P(b)=7/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=9/58=0.155；

设计：P(c)=10/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=10/58=0.172；

材料、设备：P(d)=7/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=7/58=0.121；

项目人员：P(e)=9/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=9/58=0.155；

施工过程：P(f)=9/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=9/58=0.155；

第三方：P(g)=7/7÷(9/7+7/7+10/7+7/7+9/7+9/7+7/7)=7/58=0.121；

从结果可以看出，设计因素所占的比重最大，因此设计因素对风险事故的影响最大，其次是自然环境、勘察、项目人员和施工过程因素，最后是材料设备和第三方所占的比重最小。

4.3 基于粗集理论的风险因素权重确定

粗集理论是一种对客观数据挖掘一种技术，客观性比较强，但是在先前经验知识方面理论性不是太强，另外上面我们已经提到过在构建风险知识表达系统时，前提假设对风险事故产生直接影响的风险因素才对其赋予分值，而忽略了风险因素之间的相关性。因此本文决定将主成分分析法和粗集理论相结合，来确定最终的综合权重。而主成分分析能很好的弥补这一缺陷，主成分分析法是它通过变量变换的方法把相关的变量变为若干不相关的综合指标变量[12]，可消除评估指标之间的相关影响，实践证明指标间相关程度越高，主成分分析效果越好。可减少指标选择的工作量，对于其他评估方法，由于难以消除评估指标间的相关影响，所以选择指标时要花费不少精力，而主成分分析法由于可以消除这种相关影响，所以在指标选择上相对容易些。因此本文采取粗集理论和主成分分析法相结合的方法来确定指标的最终权重，两者的权数各占50%，如果粗集权重为P1，主成分分析法为P2，则综合权重公式为：P=0.5×P1+0.5×P2。

5 结语

本文通过搜集各类风险事故资料和进行总结分析，以此建立风险知识表达系统，进而利用粗集理论确定风险因素的比重，因为评价因素存在着相互影响而主成分分析法可以消除评价因素之间的相关性，所以确定了粗糙集理论和主成分分析法相结合的权重确定方法。由于自己调查资料的不全面性，所以可能存在着不足，但希望可以为项目风险评价决策提供一些思路和方法。