地铁荷载下隧道周围粉性土孔压的单因素试验

闫春岭 张书石 李阳阳

（安阳工学院 土木与建筑工程学院 河南安阳 455000)

1 引言

动荷载作用下孔压的变化规律是影响土体强度变化的重要因素之一，研究孔隙水压力的发展规律，一是有助于了解土体在遭受外荷载作用下附加应力的分布状况，二是进一步认识土体变形机制。因此，对循环荷载下土体的孔隙水压变化规律的研究显得尤为重要[1]。国内外一些专家学者对饱和土体在遭受动荷载作用时孔隙水压力变化规律的认识有一定了解，如Seed等[2]对饱和砂土进行了一系列三轴试验，得出了振动次数是影响孔隙水压力的增长的一个不可忽视的因素，并提出了一种计算孔压的理论表达式；Nasser等[3]对饱和的均匀松砂进行了大量的三轴试验研究，首次从能量角度对孔压增长规律进行了的解释，随后，Davis等[4]借助热力学理论建立了土体能耗和孔压增长之间的表达式；曹亚林等[5]对福建标准砂进行了大量三轴试验，从土体累积耗损能量观点，得出了孔隙水压力增长的经验表达式；谢定义等[6]对循环荷载下饱和砂土瞬时孔压变化进行了相应的研究，对孔压进行了相应的分类，并得到了孔压的计算模型表达式。Chen[7]对未扰动的饱和软黏土进行了大量的循环三轴试验，研究了振动频率对孔隙水压力的变化规律，得到了对于给定的动态应力比，存在累积孔隙水压力阈值，如低于此阈值，振动频率对孔隙水压力的影响非常小，反之，影响极大。Polito等[8]对砂土和粉性土进行了大量的循环三轴试验，对孔隙水压力采用了循环应力比及 Green-Mitchell-Polito两种模型进行了研究。Lee等[9]对不饱和砂土进行孔隙水压力三轴试验研究，得出了随着饱和度的降低，孔压值显著降低，在围压平均有效应力为30 kPa条件下，非线性变形特征略受B值影响。高军[10]通过分析动三轴试验结果，研究了孔隙水压力与累积塑性应变之间的关系；肖东辉[11]、王世彪[12]、葛世平[13]、孟凡丽[14]通过土体的循环荷载试验，研究了饱和土体的动孔压模型。

目前，随着城市化进程的推进，地铁隧道设计埋深大多位于或穿越粉性土层。本文参考国内外专家学者的研究方法与成果，采用单因素试验方法，结合方差分析，系统地研究动应力幅值、振动频率及固结比对地铁荷载下粉性土孔隙水压力的影响程度和规律，该研究结果对地铁隧道土体的长期沉降预测具有重要的理论价值和实际意义。

2 室内动三轴试验

2.1 试验仪器简介

图1 GDS动三轴循环系统

试验采用英国进口多功能动态循环三轴系统GDS，如图1所示。

2.2 试验土样

试验土样取自上海地铁10号线国权路站附近②3层粉性土，其埋深为12.5m，该土层为Qh3的滨海-河口相沉积，厚约10m。粉性土的基本物理力学参数见表1。

表1 土体的基本物理力学指标

2.3 试验准备工作

首先切取土样，试样加工制成高为10 cm，直径为5 cm的圆柱土体；其次为了使试样表面水力贯通，便于渗透，黏贴滤纸条，宽度约1 cm，并均匀布置在试样两侧（3～4条），同时在两端顶部分别贴上圆形滤纸；再次小心谨慎套乳胶膜，保证不扰动试验为准；最后，往压力仓注纯净水，开始试验。

3 单因素试验设计及结果

在本次试验中，考虑地铁影响土体孔隙水压力的因素为振动频率、动应力幅值及固结比。根据文献[15]，本次试验采用的频率为0.5 Hz，1.5 Hz，2.5 Hz；根据文献[16]，动应力幅值取20 kPa，30 kPa，40 kPa；根据土样本身的物理力学指标及工程实际经验，将试验中固结比取1，2.5，3.3[17]。最终试验结果列于表2。

表2 地铁荷载下粉性土的孔隙水压力

4 试验结果的方差分析

设某单因素A有r个水平A1，A2，…，Ar，在每个水平下分别做了ni（i=1，2，…，r)次试验，按数理统计的方法，单因素方差分析步骤如下：

4.1 计算平均值

所以组内和为：

4.2 计算离差平方和

（1）总离差平方和

ST表示各试验值与总平均值的偏差的平方和。

（2）组间离差平方和

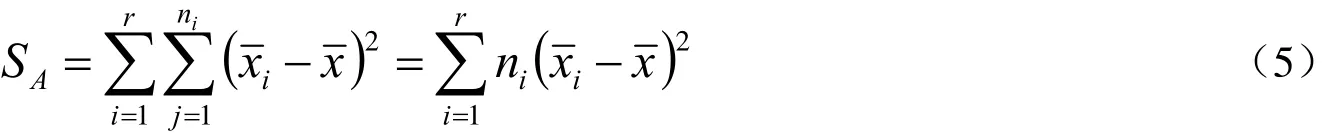
SA表示因素A组间离差平方和。

（3）组内离差平方和

Se表示组内离差平方和。

4.3 计算自由度

（1）总自由度

（2）组间自由度

（3）组内自由度

式中，dfT为总自由度；dfA为组间自由度；dfe为组内自由度。

4.4 F检验

将各因素的平均离差的平方和与误差的平均离差的平方和分别相比，得到F值

FA为因素A的F值。如果，则认为因素A对试验结果有显著影响，否则认为因素A对试验结果没有显著影响。

4.5 各因素对孔隙水压力的方差分析

按上述步骤，对表2的数据进行计算，考虑工程中的实用性，给出检验水平α=0.05及α=0.01，从F分布表中查得F0.05（2，6）=5.14，F0.01（2，6）=10.93。结果列于表3～表5。从表3～表5中可看出，振动频率、动应力幅值及固结比对孔隙水压力均有非常显著的影响。

表3 振动频率对孔隙水压力的方差分析

表4 动应力幅值对孔隙水压力的方差分析

表5 固结比对孔隙水压力的方差分析

图2 不同频率的孔隙水压力与振动次数关系

4.6 各因素对孔隙水压力的分析

图2为动应力幅值为30 kPa，固结比K=2.5，不同频率的孔隙水压力与振动次数关系曲线，从图4可以看出，随着振动次数的增加，粉性土的孔隙水压力逐渐增大。在相同振动次数下，低频（0.5 Hz）产生孔隙水压力较大，高频（2.5 Hz）产生的孔隙水压力较小。

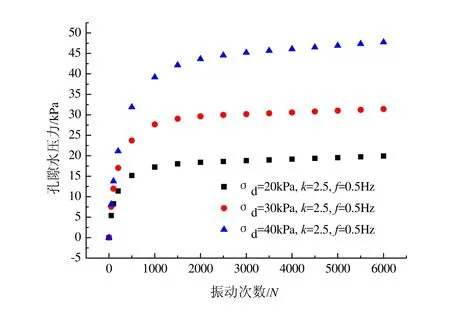
图3 不同荷载幅值的孔隙水压力与振动次数关系

图3为固结比为2.5，频率为0.5 Hz，不同荷载幅值的孔隙水压力与振动次数关系曲线，由图5可知，当荷载幅值较小时，随着振动次数的增加，孔压逐渐上升，但上升的速率较小；当作用较大的荷载幅值时，土体将在较短的时间内产生较大的孔压。

图4为动应力幅值为30 kPa，振动频率为0.5 Hz，不同固结比的孔压随振动次数的关系曲线，本文采用的固结比分别为1，2.5及3.3，轴压一定，固结比越大，产生的孔压就越大。

图4 不同固结比的孔压随振动次数的关系

5 结论

通过对上海地铁10号线附近的粉性土进行多功能GDS循环三轴试验，考虑了振动频率、动应力幅值及固结比等因素对孔隙水的影响，得到：

（1）相同振动频率及固结比条件下，动应力幅值越大，产生的孔隙水压力就越大；相同动应力幅值及固结比条件下，频率越小，产生的孔隙水压力就越大；相同动应力幅值及振动频率下，固结比越大，产生的孔隙水压力越大。

（2）从孔隙水压力与振动次数的关系中可以看出，孔隙水压力经过快速增长-缓慢增长-衰减稳定三个阶段的变化过程，因此，地铁运营初期是防止孔压增长控制的重点。

（3）通过单因素及方差分析方法，得到振动频率、动应力幅值及固结比均对孔压有非常显著的影响。