勾连除法 整体架构
——“认识平均分”整体教学研究
广东深圳市光明新爱华小学 赖琪雯
“平均分”是小学数学教学中的一个重要概念,与除法运算、除法问题的解决、分数的认识等内容密切相关。各版本教材都将“平均分”编排在“除法的初步认识”之前,在认识平均分的两种现实原型(等分、包含)之后引入除法,提出“(平均分的情况)可以用除法表示”。
这样的设置引发笔者思考:平均分和除法之间有什么关系? 为什么除法可以表示平均分? 从平均分过渡到除法的认识,儿童理解吗? 在《平均分》的具体教学中,教师可以怎样为除法意义的认识做铺垫呢?
一、教材分析与备课思考
纵观各版本教材,“平均分”这一内容的编排有以下共同点:在情境选取上,采用分水果、分糖果、分圆片等可操作性强的具象情境;在概念引入和下定义时,呈现均分与不均分的情境图加以对比,并用“每份分得同/一样多”来定义平均分;在概念理解方面,借助卡通人物的语言、虚线、箭头等形式凸显平均分的过程;在处理平均分两种现实原型时,先呈现“等分”的例子,再呈现“包含”的例子;在引入除法时,结合均分的情境直接呈现除法算式和各部分名称,提出“(平均分)可以用除法来表示”。
教材虽如此编排,但若实际教学也这样引入除法,就会让人感觉中间断了一截。要想让平均分与除法的联系更紧密、过渡更顺畅,势必要先对两者的本质进行挖掘。关于平均分,它是一个兼具过程和结果的二重性概念,既表述了分的过程——等分或包含,又概括了分的结果——每份分得同样多。只要是把一个整体平均分成若干相同的部分,这个过程/结果就是平均分。除法,从运算的角度上说,它是减数相同的连减的简便运算。至此,从 “分”和“减”这两个字眼,我们终于找到了平均分与除法之间的关联。基于此,笔者进行了整体教学探索与尝试。
二、整体教学“三步走”思路
第一步:动手操作,思维外显,初识概念
课时主要目标:结合情境,通过动手操作,经历分的过程,认识平均分的两种现实原型,初步理解平均分的含义。
【教学片段一:等分】
师:有一堆萝卜,要分给3只小兔,每只小兔分到的要一样多,怎么分?
(学生事先不知道萝卜的总数量,用小棒代替萝卜,独立操作,再展示交流。)
生1每次给每只小兔各分1根(一根一根地分),分了4次;生2两根两根地分,分了2次;生3先各分3根,剩下的刚好各分1根,分了2次;生4先数出萝卜的数量是12根,再想乘法口诀三几十二,直接给每只小兔分4根,分了1次。
师:你们的方法各不相同,但分的时候却有一样的地方。
生:(要么)一根一根,(要么)两根两根,(要么)三根三根,没有一下一根、一下两根、一下三根的。
师:也就是说,要想每只小兔最后分到的一样多,就得让它们每次分到的一样多。
【教学片段二:包含】
师:有15根骨头,每只小狗分3根,可以分给几只小狗?
生:老师,有几只小狗啊? (学生受“等分”情境的影响,对这种问题的理解需要指导)
(生用小棒代替骨头,独立操作,再展示交流)
师:小朋友们的方法都一样,都是3根3根地拿,怎么不像分萝卜那样1根1根、2根2根地分呢?
生:因为每只小狗要3根。
(初步感知两种分物活动的不同)
【教学片段三:认识平均分】
师:分萝卜和分骨头,分的总数不同,兔子、小狗的数量也不同,但有什么相同的地方?
生2:每只小兔分到4根,每只小狗分到3根,小兔和小兔一样多,小狗和小狗一样多。
师:像这样,每只小兔分到的一样多,每只小狗分到的一样多,每份分得一样多,叫作平均分。
设计意图:本课时主要通过经历等分、包含这两种情况的分物过程,再勾连其相同之处,初步体会平均分的含义。
第二步:多元表征,沟通切换,体会内涵
课时主要目标:在操作的基础上,通过多元表征方式凸显分的过程、表达分的结果,深入理解平均分的内涵。
【教学片段一:图画表征】
师:上节课,小朋友们通过摆小棒、互相交流,能让小伙伴清楚自己是怎么分萝卜的,如果让你用画的方式来分,可以吗? (生自主画图)
(2)变量概念的理解,包含变量名、变量值和数据类型。以餐厅里的包间作为类比物,变量名相当于包间名称(牡丹厅),数据类型相当于包间类型(大、中、小)。变量值相当于在该包间用餐的12位客人。
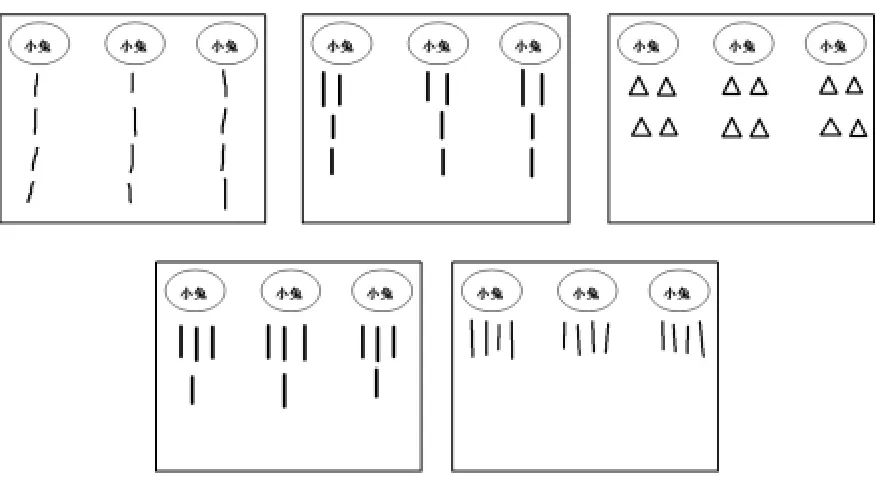
图1 学生画图表示分萝卜的过程(部分作品)
师:通过图画,你能读懂这些小朋友是怎么分萝卜的吗?
(同样,分骨头的过程也可以用图画来表示。)
【教学片段二:语言表征】
师:回忆分萝卜、分骨头的过程,我们分别分什么? 怎么分? 结果是什么? 请你和小朋友们交流这3个问题。
生:分萝卜,1根1根地分,或2根2根地分,……最后每只小兔分到4根萝卜。
生:分骨头,每只小狗分3根,3根3根地拿,最后分给5只小狗。
师引导提炼:
12根萝卜,平均分给3只小兔,每只小兔分到(4)根。
15根骨头,每只小狗分3根,可以分给(5)只小狗。
【教学片段三:算式表征】
师:通过动手摆、动笔画、动口说,小朋友们都把平均分弄清楚了。其实,平均分的过程还可以用算式记录下来。
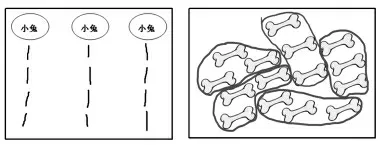
图2 等分(左)和包含(右)
等分:每次给每只小兔分1根,每次分掉3根,12-3-3-3-3=0。12连续减去4个3后,没有剩余。所以,每只小兔分到4根萝卜。
包含:每只小狗分3根,15-3-3-3-3-3=0。15连续减去5个3后,没有剩余。所以,可以分给5只小狗。
设计意图:本课时是在初步认识平均分后,在较熟练操作的基础上,探索呈现图画、语言、算式多元表征,并互相勾连,加深对平均分内涵的认识。其中,图画表征是基础,用语言清晰地表达出图画意思是关键,而算式是较高层次的抽象概括,能检验学生是否理解平均分的内涵。这三种表征方式都能为后面除法的引入做铺垫。
第三步:增大数目,灵活应用,初步体验试商过程
课时主要目标:增大总体的数目,通过多次尝试,能灵活选取每次分的数量,从而减少分的次数,掌握大数目平均分的方法,为今后试商做铺垫。
【教学片段】
师:50颗糖果平均分给4个人,每人得到几颗?你是怎么分的?
(生用50根小棒代替糖果实际操作,可能出现不同的分法:1根1根地分、2根2根地分、3根3根地分、5根5根地分、10根10根地分,等等。)
师:当分的物品数量越来越多,再像这样用小棒操作会怎么样?
生:麻烦,出错……
师:你能不能用表格记录的方式,把每次分给每个小朋友的糖果数量记录下来?
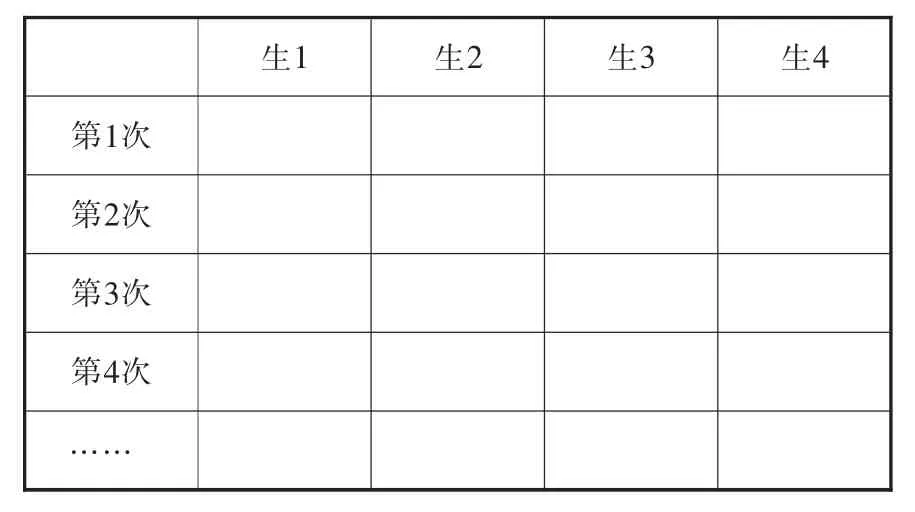
生1 生2 生3 生4第1次第2次第3次第4次……
设计意图:本课时通过经历大数目物品的平均分过程,对比不同学生每次分糖的数量、分的总次数,形成方法:第一次要用较大的计数单位,尽可能多分一些,使剩下的尽可能少一些。每次分掉多少、剩下多少,可以用数数的知识或乘、加运算的知识。这其实是试商的过程,意在拓展学生对平均分的认识,灵活应用方法,同时培养数感,为今后除法试商做铺垫。
三、整体教学过程实施策略
不同教材在编排“平均分”时,都安排了不少于两课时的内容。在关联前后、整体教学的过程中,教师应注重以下三条策略,帮助学生深入理解平均分的内涵,并顺利过渡到除法意义的认识。
1.注重情境选取,提供具象可操作情境
情境是数学的承重墙,合理恰当的数学情境能为学生提供丰富的学习资源,激发学生的学习兴趣。二年级学生心中虽已有了抽象的概念,但其思维仍处于具体运算阶段,需要具体事物的支撑。在平均分的概念教学中,教师要注重情境选取,提供具象的、可操作的情境,使情境与数学问题有机整合,从而帮助学生理解概念。例如:教师可以设计动物乐园美食分享会的故事情境,给小狗、小兔、松鼠、小猴等动物提供骨头、萝卜、松果、桃子等食物,用连贯的分食物情境串联一节课,设计多次分物活动。在情境的支撑下,学生能直观地理解数学问题、明确探究任务,在解决问题时也有话可说、有理可循。
2.注重过程经历,积累基本活动经验
动手操作是新课程倡导的重要学习方式之一,是学生建构知识的重要方法,对发展学生的“创新精神和实践能力”具有重要意义。二年级学生虽然已经有了较强的“平分”意识,在生活中也积累了较丰富的“平分”经验,但他们大多满足于追求平分的结果,而对分配过程的关注度不够、表达还很模糊。上文提到,平均分是一个二重性概念,如果只关注结果,而不充分经历分配的过程,没有积累分物的活动经验,学生就难以建构平均分的意义和概念,也不利于后续将平均分转化成除法,建立平均分与除法之间的联结。更有甚者,缺乏对过程的关注还会导致后续遇到大数目物品的平均分时无从下手。因此,教师在教学时应注重过程经历,帮助学生积累基本活动经验、探寻平均分的概念本质。
3.注重多元表征,“图—话—式”多渠道表达
数学概念是生活中事物抽象概括的结果,小学生建构概念离不开多种表征方式的辅助。在平均分的教学中,我们不难发现,学生们都会操作、会分物,也在教师的引导下学会了画图表达。但是,有时学生会画图,并不代表他能用语言表述。平均分有三要素,即均分主体、均分方法、均分结果,这三要素对应了总数、份数和每份数,也与除法算式中的被除数、除数、商相关联。因此,在会操作、会画图之后,还要引导学生用语言清晰地提炼这三个问题。这样有助于学生将动手操作、动笔涂画、动口表达有机结合,将模糊的感知转化为内部的思维活动。
其次,算式表征是从操作到直观图画,再到清晰的语言之后更高层次的抽象概括。平均分和除法算式的勾连在于,分物的过程是从总体里去掉部分的过程,也就是做减法;而除法是减数相同的连减的简便运算。因此,在平均分概念的建构过程中,算式表征十分重要,有助于学生从平均分转化到除法,从而辅助理解除法运算的意义。

