正交复用二进制偏移载波双环跟踪技术
任宇飞,卢晓春,冯瑞
(1. 中国科学院大学 电子电气与工程学院,北京 100049;2. 中国科学院国家授时中心,陕西 西安 710600;3. 航天工程大学 电子与光学工程系,北京 101416)
0 引 言
正交复用二进制偏移载波(QMBOC)信号[1]于2010年被姚铮等人提出.区别于欧洲Galileo的CBOC信号的多电平处理[2]和美国GPS L1C中TMBOC信号的时分复用[3]处理,QMBOC信号将复用信号调制在正交载波之上,实现了多信号分量的正交使用,并在北斗三号卫星导航系统(BDS-3)中作为新一代导航信号B1C的导频分量使用[4].QMBOC信号在B1C中完成信号同步工作,并得到伪距测量值,同时将同步信息传送到数据分量从而解调出导航电文信息[5].
由于QMBOC信号中存在的多峰性和多个过零点,因而提高跟踪精度的首要任务就是消除模糊度.现有的解决思路一般有两种,一种是致力于消除副载波带来的影响,包含1) 2N法,通过正交两路构成2N个相关器来构造相应的鉴别曲线;2) 峰跳法(Bump-Jump)[6],属于误锁恢复装置,通过添加额外的远超前和远滞后相关器比较实现跟踪;3)边带消除法,又被称为自相关边峰消除技术(ASPeCT)[7],利用伪码与信号的互相关与信号自相关函数的数学关系,尽可能地减小跟踪的模糊度.另一种思路就是双环跟踪估计法,即从BOC信号调制的原理出发,将整个调制过程逆向化,分别对伪码相位和副载波相位进行跟踪.文献[4]在探讨双环跟踪的理论中得到的闭合形式的近似分析,提出了一种带宽相关的准最佳鉴别器参数选择理论,以简化接收机设计者的设计工作;文献[8]在研究了考虑一般二维跟踪环路噪声和多径环境下的相关函数的关键性质和理论跟踪的性能分析,并考虑了局部副载波波形失配和前端频带限制的影响.在此基础上衍生的相干边带处理(CSB)[9]方法也是双环跟踪估计方法的延伸.
本文首先对QMBOC信号构成和接收模型做了简要分析,然后比较了跟踪消除的方法,在双环跟踪的基础上结合BOC(1,1)信号对QMBOC进行跟踪,并采用副载波联合跟踪与之对比,并进行了仿真模拟,为下一步B1C信号同步理论的研究提供了理论依据.
1 QMBOC信号接收模型
QMBOC调制信号中含有BOC(1,1)分量和BOC(6,1)分量,根据功率合成的原则,QMBOC基带信号可以表示为
(1)
QMBOC信号中的两个分量置于正交的载波上,根据文献[4],BOC(1,1)与BOC(6,1)分量的比值为29∶4,按照此功率比结合起来,合成了导频分量QMBOC(6,1,4/33)信号.则该QMBOC信号的自相关函数可表示为

(2)
不同调制方式的自相关函数比较如图1所示

图1 不同调制方式下的相关函数
区别于BPSK信号的自相关函数的单峰特性,BOC族信号的相关函数均为2k-1(k为调制阶数),BOC(1,1)与QMBOC信号峰数少且平缓,BOC(6,1)峰数多且尖锐.则QMBOC信号功率谱密度可表示为

(3)
相应的功率谱密度图为图2.

图2 不同调制方式下的功率谱密度
信号中BOC(1,1)分量占29/33,因而QMBOC信号的主瓣与BOC(1,1)近似重合,而剩余的BOC(6,1)分量包含在±6×1.023 MHz处的功率谱.信号经过调制、传输到接收机前端得到的信号形式为
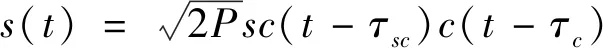
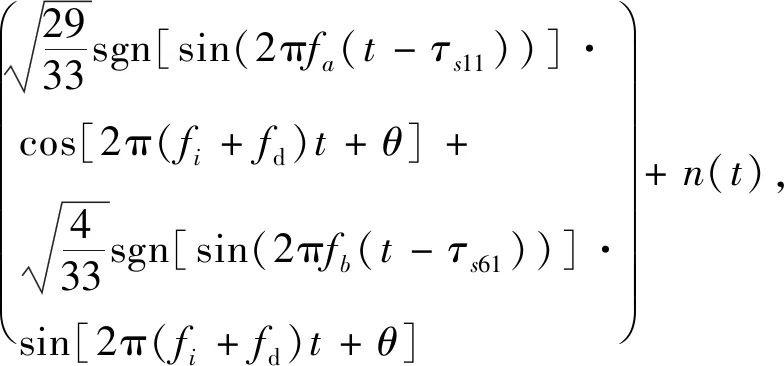
(4)
式中:P为信号的功率;sc(t)为子码扩频码;c(t)为主码扩频码;τc为主码延迟;τsc为子码延迟;sign(sin(·))为方波副载波;fa表示BOC(1,1)副载波的频率1.023 MHz;fb表示BOC(6,1)副载波的频率6.138 MHz;τs11为BOC(1,1)副载波延迟;τs61为BOC(6,1)副载波延迟;cos(·)和sin(·)为正交载波;θ为载波相位;fi为载波频率,fd为多普勒频偏;n(t)为高斯白噪声(WGN).这样了就建立了QMBOC信号的接收模型.
2 QMBOC信号跟踪方法
引言中简述了2N法,Bump-Jump法和ASPeCT法.作为跟踪处理的主要方法,ASPeCT在BOC类信号中广泛使用.QMBOC信号可以近似看做是BOC(1,1)信号,因而满足ASPeCT所局限的使用范围[7].同时,在信号与伪码的互相关运算可以采用BOC(1,1)替代QMBOC信号进行,如图3所示.

图3 ASPeCT算法原理分析
由图3得知,BOC(1,1)与伪码的互相关函数与QMBOC信号自相关函数的码片位置相同,幅度略大于自相关函数的副峰,根据算法的原理可以得到
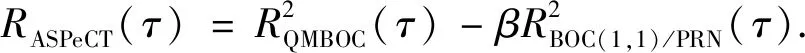
(5)
式中:R(·)为相关值;β为系数参数.构造出的副峰消除的函数如图4所示.

图4 QMBOC信号ASPeCT算法结果
图4所示的结果提升了相关函数峰的斜率,提升了鉴相的精度,但是依然存在较小幅度的模糊问题,跟踪模糊消除效果有限.
3 双环跟踪的分析
上述对于QMBOC信号跟踪模糊消除是基于对信号整体的处理,没有从信号调制原理上进行分析研究,在估计信号的时延上默认伪码和副载波是同一数值.这样的分析存在两个问题:1)跟踪时没有很好地消除模糊度,简单地将伪码与副载波看成整体的研究甚至会恶化跟踪的精度;2)没有体现出信号中多个副载波存在的优势.
QMBOC信号调制就是伪码调制副载波再调制到载波的过程,在假设载波同步的情况下,接收信号与本地信号的相关可以表示为[10]
R(τ-τc,τ-τs)=
(6)

根据这个原理, Hodgart[11]于2007年提出了双环跟踪的研究方法,将BOC信号的伪码和副载波分为两个独立的参量,接收机内部单独构建两个环路伪码延迟锁定环(DLL)和副载波延迟锁定环(SLL)分别对其跟踪,称为双环跟踪(DET)方法.将QMBOC信号带入到式(6)中,得到的二维相关函数如图5所示.
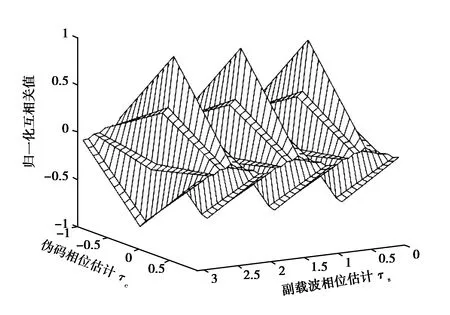
图5 QMBOC信号的二维相关函数

图6 QMBOC信号的副载波相关
副载波是以2Ts为周期的扩展,即连续的相关结果.同时,根据文献[12]的码环鉴相原理,得到非相干幅值早迟相减的表达式为

(7)
因而采用式(7)对伪码和副载波进行相应的鉴相计算.在跟踪鉴相的过程中会存在模糊,SLL中不同相关器间距下的副载波早迟鉴相如图7所示.

图7 副载波维度的相关函数值


图8 伪码维度的相关函数值
伪码维度上的相关与直扩信号的相关相同,图中含有正负结果是受副载波相关影响.在DLL上不同相关器间距下伪码鉴相曲线如图9所示.

图9 伪码维度的相关函数值
伪码鉴相在δ≤0.5的间距范围内,鉴相的斜率是一致的,间距越大幅值越大,δ=0.5得到鉴相的最大区间.继续增大至δ=1时,幅值不变,斜率值下降.
QMBOC信号在伪码和副载波两个不同的维度上呈现出各自的特点:伪码维度上的相关峰值仅体现伪码的相关性,尖峰宽精确度低但是无模糊;而副载波维度上由于受更高的频率调制,尖峰窄精确度高但是有模糊存在,存在多个峰值.由此得到伪码与副载波鉴相比较如图10所示.
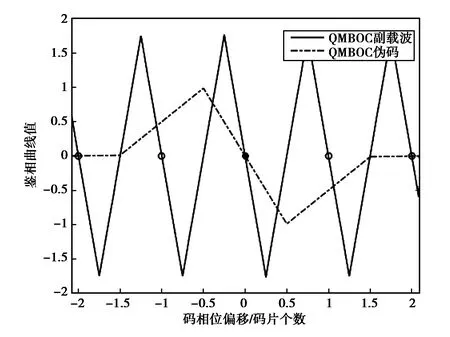
图10 伪码与副载波的鉴相比较
图中的圆圈表示为误锁点,实心圆圈表示跟踪鉴相的准确位置,利用上述双环的运算可以实现信号跟踪的高精度性和无模糊性.
将伪码和副载波相位估计为两个独立的参量,其中SLL锁定环路中的任何一个峰值都可以创建稳定的锁定点,通过与DLL粗略估计值的连续比较,使得跟踪在该维度中的精确相关保持在正确的整数值,根据两者的关系得知:
(8)
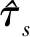

(9)

上述研究分析是将QMBOC信号的副载波视为一个整体进行的探讨.事实上,QMBOC包含的BOC(1,1)和BOC(6,1)分量就是根据不同的应用要求而区分开.前者范围广,但是精度有限,是在跟踪初期以及恶劣条件下主要使用的信号分量,后者精度高,但是所需要的相关器间距等要求更为苛刻,需要在跟踪稳定后有进一步精度要求时使用.
设信号的采样率为32×1.023 MHz,相关器间距设为1/4码片,积分周期为10 ms,得到各分量下的副载波鉴相比较如图11所示.点线所围成的虚框指示BOC(1,1)副载波的鉴相范围,为-1/8~1/8码片,虚线框指示了BOC(6,1)副载波的鉴相范围,为-0.02~0.02码片.两者的鉴相区间相差6倍.
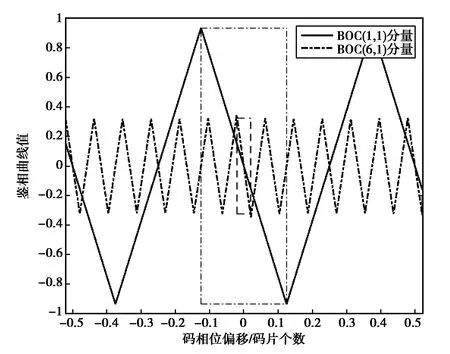
图11 不同分量副载波的鉴相曲线
图11的比较中BOC(6,1)副载波鉴相精度优于BOC(1,1),但由于在QMBOC信号中BOC(6,1)分占比只有4/33,只在有高精度要求的情况下采用,通常的BOC(1,1)信号下的DET即可实现QMBOC信号各分量的同步.根据上述的原理得到的双副载波跟踪的结构如图12所示.

图12 双环跟踪研究方法原理图
图中的环路除了载波跟踪环路与伪码跟踪环路以外,包含BOC(1,1)和BOC(6,1)信号副载波跟踪环路,虚线表示BOC(6,1)跟踪环路可以进行选择,即可以采用BOC(1,1)副载波环路、BOC(6,1)副载波环路以及联合副载波环路三种方式组合进行处理.图中输入的中频信号与载波NCO相乘去掉载波后,分为两个支路,一个支路乘以即时支路副载波进入伪码的跟踪环路,伪码环路有三个支路早中迟,其中,伪码即时支路输出作为载波鉴相的结果,可表示为[13]
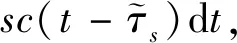
(10)

伪码环路的早-迟支路进行积分清除运算,结果可表示为
(11)
式中:δc为伪码相关器的间距,其余变量见式(10).早迟伪码经过鉴相和DLL滤波器的输出控制伪码NCO的参数,从而调整伪码的生成.
副载波环支路中下变频信号与即时伪码相乘,分为早迟两路进行副载波环的鉴相,积分结果可表示为
(12)
(13)
式中:δs为BOC(1,1)副载波相关器的间距;δs61为BOC(6,1)副载波相关器的间距,其余变量见式(9).副载波环路结果经过鉴相和滤波器的输出控制副载波NCO的参数,同时根据式(8)和式(9)的反馈进一步提高伪码跟踪的精度.
图12中QMBOC信号DET中既含有BOC(1,1)又有BOC(6,1)分量,若采用BOC(1,1)分量进行跟踪,则采用式(11)和式(12)进行双环估计;若采用副载波联合跟踪则应结合式(13)并按以下比例生成估计值
(14)
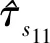
4 算法仿真验证
对本文提出的进行仿真验证分析.以BDS-3系统20号卫星的B1C调制信号为例,参数设置如表1所示.

表1 信号跟踪仿真参数
4.1 不同分量下的跟踪仿真
由于QMBOC信号中包含有BOC(1,1)和BOC(6,1)分量,分别采用两个分量的双环方法对QMBOC信号进行跟踪仿真.对于载波跟踪,根据图12的原理图分别采用BOC(1,1)和BOC(6,1)分量得到的结果如图13所示.

图13 载波环路跟踪结果
图中的载波跟踪环路在0.1 s以后各分量跟踪均趋于稳定,性能相近.而在原理图分析的基础上结合式(11)对于伪码相位的估计得到的跟踪结果如图14所示.

图14 伪码环路跟踪结果
伪码跟踪环路中的BOC(1,1)跟踪阶跃较大,但在0.2 s后的稳定跟踪中误差起伏较小.BOC(6,1)跟踪中没有明显的跟踪阶跃,但稳定跟踪后起伏仍然较大.这也体现了BOC(6,1)实现伪码跟踪所需要的条件更为苛刻.
在另一个副载波维度跟踪分析中,根据图11的比较可知BOC(1,1)信号与BOC(6,1)信号的副载波相关器间距差异较大,在副载波环路中进行SLL鉴相需要分析不同相关器间距下跟踪效果,在间距小于10-1时固然能实现很好的稳定跟踪性能,但是存在两个问题:1)间距减小需要提升系统的采样频率,计算量加大;2)间距减小对于抗噪声性能降低,跟踪结果极易受到噪声的干扰.因而根据图11的分析并结合式(7)的鉴相公式分析,对BOC(1,1)信号采用不同间距得到的副载波跟踪如图15所示.

图15 BOC(1,1)副载波环路跟踪结果
图中的间距范围大小对副载波跟踪的误差结果影响有限,因而在双环跟踪中相关器间距取较大值,即δ=0.25.
4.2 联合跟踪仿真比较
在4.1节仿真结果基础上,根据图12中的原理图和式(14)采用BOC(1,1)和BOC(6,1)副载波进行跟踪鉴相,根据图7分析取δ=0.02为BOC(6,1)信号副载波的间距,与上述的跟踪方法作比较.载波跟踪结果如图17所示.

图17 载波环路跟踪结果
相较于ASPeCT方法,BOC(1,1)和联合双环跟踪在稳定跟踪时得到的误差均值小约40倍,跟踪精度更高.而伪码跟踪的误差比较如图18所示.
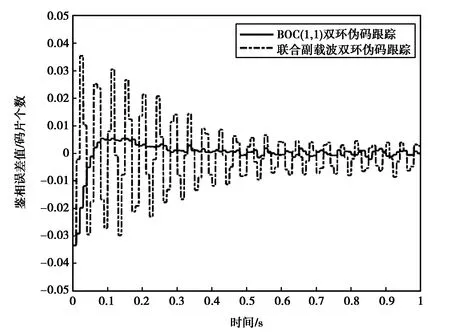
图18 伪码环路跟踪结果
图中三种方法跟踪结果比较而言,BOC(1,1)DET优于联合副载波跟踪方法和ASPeCT方法,为了更进一步的量化分析,在此分析基础上,对不同载噪比下的跟踪方法进行仿真比较,得到的伪码跟踪误差比较如图19所示.
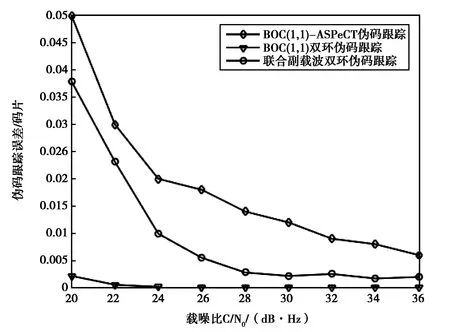
图19 伪码环路跟踪结果
图中ASPeCT算法跟踪误差最大,在载噪比大于32 dB·Hz时误差降到0.01码片以内,而联合副载波跟踪在低于26 dB·Hz时的跟踪误差大于0.005码片,而当载噪比升高跟踪稳定后的误差在0.002码片,BOC(1,1)双环跟踪算法误差最小,在大于24 dB·Hz趋近于0.因而通过比较可知,在较低的噪声环境下BOC(1,1)双环跟踪的效果优于其他两种跟踪结果.
5 结束语
本文对正交复用二进制偏移载波QMBOC信号结构及其跟踪原理进行了研究分析,得到以下结论:
1)对常用的跟踪消除的方法ASPeCT等进行了理论分析,该方法消除了部分跟踪模糊,但还存在一定的模糊残余;
2)针对现阶段研究较为广泛的DET进行了理论推导,分析了码相位估计模糊消除的思路,重点比较了QMBOC下的BOC(1,1)和BOC(6,1)分量鉴相的相关间距差异,得到BOC(6,1)信号的副载波跟踪精度更高,但需要更小的相关间距及严苛的跟踪条件,而BOC(1,1)信号跟踪范围较大,是处理QMBOC跟踪时的主要分量;
3)为简化跟踪环路采用BOC(1,1)双环跟踪接收QMBOC信号,加之在分析了副载波环路的基础上进一步引入副载波联合跟踪,并给出了原理分析图和公式说明.仿真表明在载噪比大于24 dB·Hz时BOC(1,1)信号的码跟踪误差趋近于零,而联合跟踪误差在载噪比大于28 dB·Hz时小于0.005,因而BOC(1,1)双环跟踪在低载噪比的伪码跟踪精度上优于联合跟踪的方法,在应用中可采用该方法进行相应的处理.
但是,在跟踪研究中只加入了的WGN,对深入研究采用联合副载波环进行稳定跟踪分析有限,没有进一步探讨高精度跟踪的适用条件和范围,在下一步研究中还有待进一步的研究与分析.

