基于盲信号分离的机载VDB接收机同频干扰抑制

倪育德,李许光

(1.中国民航大学 电子信息与自动化学院,天津 300300;2.中国民用航空局 民航航空器适航审定技术重点实验室,天津 300300)

0 引 言

机载甚高频数据广播(VDB)接收机是陆基增强系统(GBAS)的重要组成部分,它接收GBAS地面站发送的VDB信号,通过解码和数据处理得到最后进近航段数据和相应的改正信息,从而引导飞机完成精密进近和着陆. 随着民用航空的迅猛发展,飞机的数量越来越多,机载航空电子系统受到干扰的情况也越来越多,人们对其所受到的干扰也进行了大量分析研究,其中不乏“黑广播”、恐怖袭击等人为因素造成的干扰.

盲信号分离是从接收信号中恢复未知源信号的有效方法,应用领域非常广泛,在干扰抑制方面也得到了一定的应用[1-6],但还未发现利用盲信号分离进行机载VDB接收机干扰抑制的公开报道. 本文对美国航空无线电技术委员会(RTCA)颁布的《GPS局域增强系统机载设备最低运行性能标准》(DO-253C)[7]中提到的机载GBAS VDB接收机所受到的同频干扰进行分析,提出了一种基于盲信号分离抑制机载VDB接收机同频干扰的方法,

即利用盲信号分离算法对机载VDB接收机接收到的混合信号进行分离,然后通过识别解码数据中的机场标识(ID),得到所需的信号,从而达到抑制VDB同频干扰信号的目的.

1 VDB信号特征

VDB信号采用时分多址工作方式[8],其帧结构如图1所示. 每帧有8个时隙,每个时隙(62.5 ms)均包含88 bit的训练序列,总共分为五部分,其中,第一部分为15 bit的功率稳定性码元,第二部分为48 bit的同步码元,第三部分为3 bit的站隙标识符,第四部分为17 bit的发送长度,第五部分为5 bit的练习序列的前向纠错. VDB时隙中发送的应用数据长度是可变的,最长为1776 bit,里面包含了所有的最后进近航段信息和差分校正信息. VDB信号采用差分8相移键控(D8PSK)的调制方式,数据传输速率为10 500 symbol/s,编码时首先将二进制数据组合成字符,每个字符由3个连续的二进制数据组成,之后将字符转换成D8PSK信号.

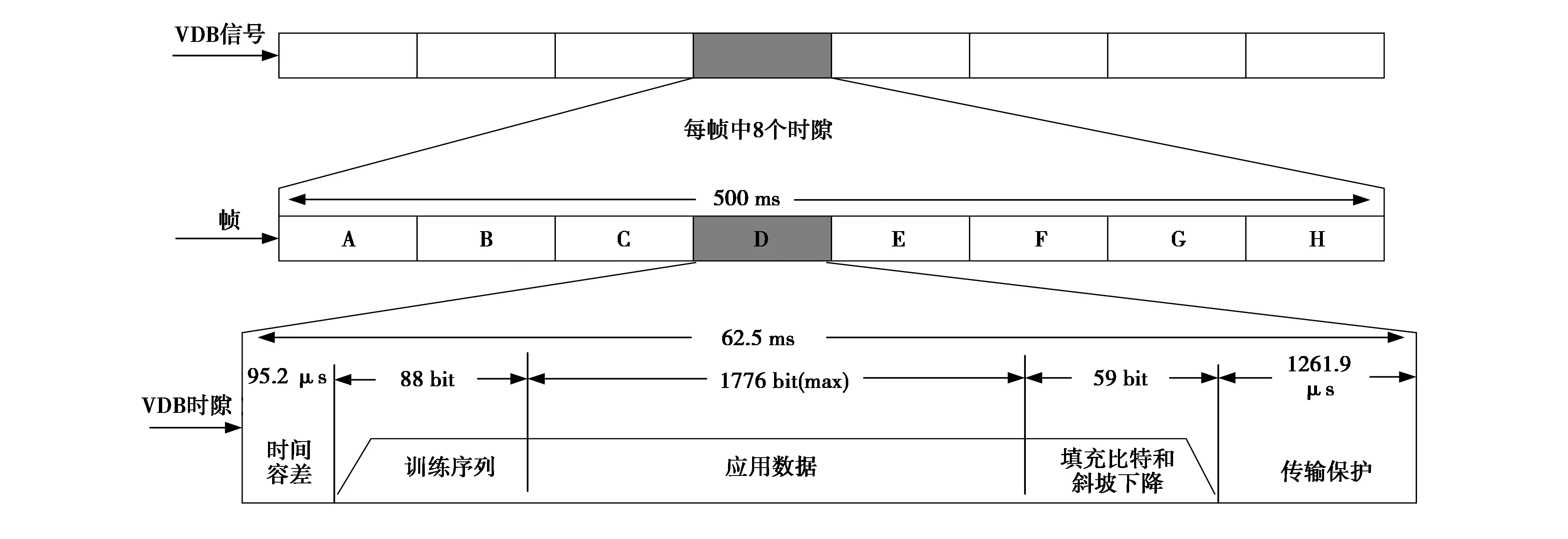
图1 VDB的帧结构

2 算法原理及流程

2.1 VDB信号混合模型

假设机载VDB接收机接收到的观测信号是由GBAS地面站产生的期望VDB信号和有意或无意产生的干扰VDB信号的混合信号,观测信号与源信号之间是线性关系,那么机载VDB接收机的输出信号也是线性混合信号. 这里假设机载GBAS VDB接收机接收到的观测信号为期望VDB信号和一个干扰VDB信号以及噪声的混合信号,即

x(t)=As(t)+n(t),

(1)

式中:x(t)=(x1(t),x2(t))T为观测信号矩阵;s(t)=(s1(t),s2(t))T为源信号矩阵,其中s1(t)为期望VDB信号,s2(t)为干扰VDB信号;n(t)是噪声信号矢量;A为一个可逆的矩阵.

基于盲信号分离的机载VDB接收机同频干扰抑制的实现框图如图2所示.

图2 VDB接收机同频干扰抑制实现框图

盲信号分离的实现受3个条件约束,即各个信号源相互独立,混合矩阵列满秩(即观测信号个数要大于等于源信号个数),源信号中最多只能有一个高斯分布的信号.

机载VDB接收机接收到的VDB信号是非高斯分布的独立信号,满足盲信号分离的约束条件,可以用盲信号分离算法来分离VDB信号的混合信号.

盲信号分离算法根据不同的原则,主要有3种分类方式,即根据盲信号分离所用的统计信息分类,根据盲信号分离的数学原理分类,根据源信号混合过程分类. 本文采用根据盲信号分离所用统计信息分类的算法,这类算法主要包括快速固定点(Fast ICA)算法、自然梯度算法和等变自适应分离(EASI)算法等. 其中Fast ICA算法收敛速度快、无须选步长参数、易于使用;自然梯度算法利用黎曼空间结构修正了梯度方向,为自适应算法提供了精确快速的定位,减少了算法的计算量;EASI算法是在自然梯度目标函数的基础上,将白化算法和盲分离算法结合起来,使得算法的性能与混合矩阵无关,实现相对简单,提高了算法的收敛速度.

下面研究基于这三种算法的机载VDB接收机的同频干扰抑制,并比较它们的性能.

2.2 Fast ICA算法

基于负熵的Fast ICA算法的目标函数[9]为

J(W)=[E{G(WTz)}-E{G(V)}]2.

(2)

式中:W是分离矩阵;z是对混合信号x进行去均值和白化得到的信号;V是零均值并与WTz有相同协方差矩阵的高斯随机向量;G(V)是非二次函数.

Fast ICA算法需要通过最大化以上目标函数来估计出源信号的一个独立成分,J(W)的极大值在E{G(WTz)}的极值点处取得,可通过求解下式得到

E{zg(WTz)}+βW=0.

(3)

建立如下函数

F(W)=E{zg(WTz)}+βW.

(4)

采用牛顿迭代法求解式(4),简化后可得到Fast ICA迭代公式为

W(k+1)=E{zg(WTz)}-

E{g′(WTz)}W(k).

(5)

基于Fast ICA算法的VDB信号同频干扰抑制的流程图如图3所示.

图3 基于Fast ICA算法的VDB信号同频干扰抑制流程

2.3 自然梯度算法

自然梯度算法以互信息最小化为目标函数[10-11]时有

(6)

用标准欧式梯度求导,可得

(7)

因要对概率密度函数p(y)和p(yi)进行估计,为了测量分离出的各信号之间的互信息,需要知道y(k)的高阶统计量. 对分离出的信号进行非线性变换,引入非线性函数,代入式(7)得

(8)

式中:W-T=(WT)-1为W的转置逆矩阵,g(y)表达式为

g(y(k))=

(9)

综上,可得随机梯度算法为

W(k+1)=W(k)+μ[W(k)-T-g(y)xT(k)].

(10)

(11)

由此,得到自然梯度算法

W(k+1)=W(k)+μ[W(k)-T-

g(y)yT]WTW

=W(k)+μ[I-g(y)yT]W(k),

(12)

式中:W(k)是分离矩阵;I表示单位矩阵,μ为步长因子;g(y)为非线性函数.

基于自然梯度的VDB信号同频干扰抑制流程如图4所示.

图4 基于自然梯度的VDB信号同频干扰抑制流程

2.4 EASI算法

EASI算法不需要对原始数据进行白化处理,而是将其与迭代过程合并,具有等变性. EASI算法[12]也以式(8)表示的互信息最小化为目标函数,通过采用自然梯度法优化分离矩阵,可以得到的EASI算法迭代公式为

W(k+1)=W(k)+u(I-g(y)yT+

ygT(y)-yyT)W(k).

(13)

基于EASI算法的VDB信号同频干扰抑制流程如图5所示.

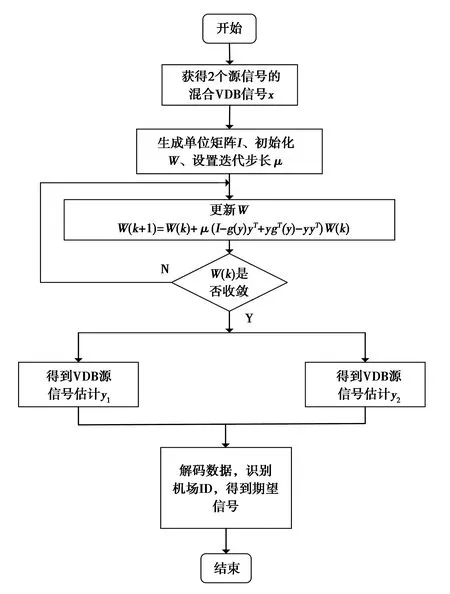
图5 基于EASI算法的VDB信号同频干扰抑制流程

3 仿真实验与分析

假设GBAS机载VDB接收机接收到的信号是期望VDB信号和干扰VDB信号的混合信号. 期望VDB信号与干扰VDB信号均为一个突发数据,长度为1 914 bit,信号传输速率为10 500 symbol/s,调制方式为D8PSK,信噪比为20 dB. 图6～10分别为VDB源信号、观测到的VDB信号以及不同盲信号分离算法分离出的VDB信号的波形图.

图6 VDB源信号

图7 观测到的VDB信号

图8 Fast ICA算法分离的VDB信号

图9 自然梯度算法分离的VDB信号

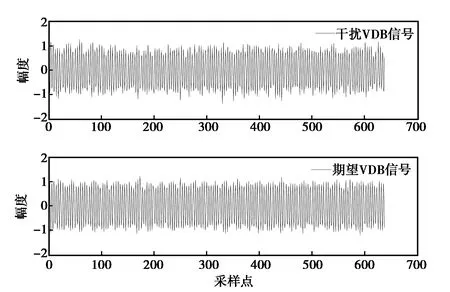
图10 EASI算法分离的VDB信号

由图8～10分离出来的信号波形可以看出,讨论的三种盲信号分离算法均可以将混合的VDB信号进行分离. 还可以看出,Fast ICA算法和EASI算法的分离效果要比自然梯度算法的分离效果好,而且盲信号分离算法分离出的信号波形具有幅度和相位不确定性以及顺序不确定性的特点. 因此,通过比较解码后的机场ID,便可剔除同频干扰信号.

下面以串音误差为性能指标[13]来对三种算法的性能进行分析. 串音误差为

(14)

式中:cij为全局传输矩阵C=WA的元素;W为分离矩阵;A为混合矩阵；maxk|cik|表示矩阵C的第i行元素绝对值的最大值；maxl|cij|表示矩阵C的第j列元素绝对值的最大值.

PI的值越小,算法的分离性能越好,当分离出的信号和源信号相同时,PI=0.

Fast ICA算法没有学习率或者其他可调参数,算法收敛的迭代次数与初始矩阵有关. 该算法经过200次随机实验的平均迭代次数为2.8次,平均串音误差值为0.052 1. 由此可以得到,Fast ICA算法的收敛速度非常快,只要迭代很少的次数就能达到收敛,而且该算法的平均串音误差值很小,说明算法的分离性能很好.

EASI算法和自然梯度算法的收敛速度和稳定性与迭代步长有关,图11是这两种算法分别在迭代步长为0.005及0.01的条件下,进行200次实验得到的平均串音误差曲线比较图.

图11 自然梯度算法和EASI算法的平均串音误差

从图11可以得到,自然梯度算法及EASI算法收敛速度与迭代步长有关. 迭代步长越大,收敛速度越快,但是算法的串音误差变化大,算法的分离性能不稳定;迭代步长越小,收敛速度越慢,但是算法的串音误差变化小,算法的分离性能比较稳定. 还可以得到,EASI算法的收敛速度和稳定性要优于自然梯度算法,但是这两种算法的收敛速度和稳定性都要比Fast ICA算法的差.

图12是三种算法分离出期望的VDB信号后,对信号进行解调得到的误码率图.

图12 三种算法误码率比较图

从图12可以得到,Fast ICA算法与EASI算法的误码率相近,前者略优于后者,而自然梯度算法的误码率最高. 这表明Fast ICA算法和EASI算法的分离性能相近,但都优于自然梯度算法. RTCA DO-253标准中要求报文的误码率要低于10-5,从图12中可以看出当信噪比达到18 dB以上时,Fast ICA算法就可以满足标准中的要求,而EASI算法和自然梯度算法需要更高的信噪比才能满足这个要求.

综上可得,Fast ICA算法的收敛速度比自然梯度算法以及EASI算法的收敛速度都要快,并且Fast ICA算法的串音误差更小,误码率更低. Fast ICA算法的综合性能要优于自然梯度算法以及EASI算法. 因此Fast ICA算法更适合用于VDB信号的同频干扰抑制.

4 结束语

本文提出采用盲信号分离算法来对GBAS机载VDB接收机的同频干扰进行抑制,利用盲信号分离算法将期望信号与干扰信号进行分离,并通过识别解码数据中的机场ID,得到我们所需要的信号,从而达到抑制干扰信号的目的. 本文采用了三种盲信号分离算法对期望信号与干扰信号进行分离,并对三种算法的性能进行了比较分析. 仿真实验表明,盲信号分离算法能够有效地将期望信号与干扰信号分开,其中Fast ICA算法相对于自然梯度算法以及EASI算法综合性能更好,更适合用于VDB信号的同频干扰抑制.