楔形桩的动力响应与试验研究
王奎华 童魏烽 肖偲 吴斌杰
摘 要:假设桩体为弹性,桩周土体通过平面应变模型描述,利用Laplace变换和阻抗传递法求得桩顶动力响应. 对数值结果进行参数分析,讨论了桩土特性对楔形桩动力响应的影响,并且通过模型试验验证了理论的正确性. 结果表明:1)存在临界桩径比,使得楔形桩的桩底反射信号难以判读,临界桩径比随桩长增大而增大;2)楔角和桩长对楔形桩的动力响应有较大的影响,对于桩尖直径为0的小直径楔形桩,桩长对其动力响应影响不大;3)土体的剪切波速和纵向分层性对楔形桩的动力响应会产生较大影响;4)模型试验结果与理论解符合,反映规律一致.
关键字:平面应变模型;楔形桩;桩径比;时域分析;频域分析;模型试验
中图分类号:TU473.1 文献标志码:A
Abstract: The pile was supposed to be elastic and the plane-strain model was adopted to simulate the surrounding soil. By the means of Laplace transform and impedance function transfer method, the dynamic response of tapered pile was obtained. Then, by parametric method, the influence of pile and soil characteristics on the dynamic response of tapered pile was discussed. Meanwhile, the correctness of the theory was verified by model test. The results show that: 1)There is a critical pile diameter ratio at which the reflected signal from pile bottom is difficult to find, and the ratio increases as the pile grows; 2) Cone angle and pile length have a great influence on the dynamic response of tapered pile. However, in the case of small-diameter pile with a zero-diameter end, pile length doesn't have an obvious influence;3) Shear wave velocity of soil and vertical distribution of soil have a great influence on the dynamic response of tapered pile; 4) Good agreement is shown between experimental and theoretical results.
Key words: plane-strain model;tapered pile;pile diameter ratio;time domain analysis;frequency domain analysis;model tests
楔形樁是20世纪末起源于前苏联的一种桩型,上大下小的特殊几何特性能使桩土作用发挥得更为充分. 特殊地,当桩底面积趋向于0时桩身呈锥形,此类桩型能较大地加快施工速度[1]. 近年来,国内外学者通过现场试验、理论分析、有限元分析等手段,对楔形桩的承载特性做了大量研究. Kodikara等[2]通过理论分析得出了打入式楔形桩的承载性能更佳的结论. 刘杰等[3]通过模型试验研究验证了楔形桩的承载优越性. 另一方面,楔形桩的动力性质研究没有足够深入.
传统管桩的动力响应方面,Novak等[4]导出了多层土体中桩基的波阻抗函数传递规律. Gough等[5]推导出了只考虑桩端土作用时基桩的自由振动特性. Koten等[6]求得了无限长桩在锤击条件下,考虑桩侧土作用时的纵向振动问题解. 以上研究都做了较大程度的简化,无法体现工程特性,近来出现了更多的求解方法和解释理论. 郭平[7]首先对低应变检测的波动原理进行了阐述,王奎华等[8-10]采用阻抗传递法研究了单桩在不同工况下的振动响应,并在楔形桩的动力问题上提出了改进的桩土作用模型. 陈安国等[11]利用差分法解得基桩在考虑桩土相互作用时的纵向振动响应解. 吴文兵等[12-14]对常见完整楔形桩的动力特性进行了初步理论分析,并考虑了挤土效应的影响. 张献民等[15]研究了桩基缺陷与传递波能量之间的关系.
在此背景下,考虑到前人[10,12-14]的理论基础已被证明正确,本文将采用积分变换法及阻抗函数传递方法,求得楔形桩在平面应变土体模型中的纵向振动响应,并辅以模型试验,对楔形桩的动力特性做进一步相关分析.
1 理论模型
1.1 模型建立与假设
根据郭平[7]、王奎华等[8-10]和吴文兵等[12-14]的相关研究,可做以下合理假设:1)桩体为一维弹性杆件,外部激励下,产生的变形为小变形,忽略桩体的径向变形;2)为实现桩径渐变,将桩身划分成足够多的桩段;3)当楔形桩取极限形态时,取底部面积为小量(如0.001 m2);4)单层土体为各向同性的黏弹性体,桩周土体为平面应变模型;5)假设任意土层在无穷远处不受激励影响,自由表面处土体的应变为0;6)桩土完全接触,接触面上应力连续.桩土系统如图1所示. 图中,将桩体分为m段,最底部的桩段标号为1,顺序往上. 为方便后续对土层性质的研究,同时将土体相应划分为同样厚度的土层.假设总桩长为L,第i段桩的桩径为r0i,高度为 Hi,且桩段顶部距离为hi. EP、ρP、AP分别表示桩体的弹性模量、密度、横截面积. 对于土体,采用平面应变模型计算桩土接触面的作用,Gs、ρs分别表示土体的剪切模量和密度.ui(r,t)表示第i层土的竖向位移函数,wi(z,t)表示第i段桩的竖向位移函数.Kb、Cb表示弹性和阻尼系数,根据Lysmer等的模拟公式:
1.3 方程求解
2.2 楔角对完整楔形桩动力响应的影响
当桩底反射信号不可见时,桩体的工作特性难以把握,需要进一步探讨. 为了对比,以下讨论中,分别对桩尖直径不为0的楔形桩(下标记为1)和桩尖直径为0的楔形桩(下标记为2)进行分析.
对于桩尖直径为0的楔形桩,控制纵向长度L = 10 m,楔角α = 1.5°、2.0°、2.5°、3.0°. 对于桩尖直径不为0的楔形桩,考虑到桩径会影响桩土作用,再固定桩身1/2高度处的樁径rm = 0.3 m. 图5显示,无论楔形桩的楔角取值如何,桩底桩径为0时均无桩底反射信号存在,而当桩底桩径不为0时,桩底反射信号峰随楔角的增大而渐弱,另外在初始激振信号之后的曲线段中,反射信号随楔角增大而逐渐抬升. 这是由于楔形桩桩身渐变,截面间不存在突变波阻抗,且当桩底桩径为0时,桩端与土作用弱,导致不存在桩底反射. 本文计算模型考虑了桩土之间的相互作用,在曲线上反映为产生与激振方向相反的下沉量. 而随着楔角的增大,截面之间存在更大的波阻抗差,相对而言有更明显的缩径表现,即产生与初始激振同向的变化趋势. 因此反射信号曲线随楔角增大而抬升.
图6显示,桩底桩径为0时,随着楔角增大,曲线震荡幅值提高,并快速衰减为一条水平直线. 桩底桩径不为0的情况下,当楔角增大时,低频区的曲线幅值升高,高频区的幅值减小. 这是因为当楔形桩桩尖直径为0时,楔角增大会引起桩身平均桩径增大,导致桩土相互作用渐弱,加剧桩身振动,在图中即表现为曲线震荡幅值随楔角增大而增大. 另外,楔角的变化会不同程度地影响同阶共振频率的移动.
2.3 纵向桩长对完整楔形桩动力响应的影响
此节,固定楔角为α = 2°,纵向长度L = 8 m、10 m、12 m、15 m,对桩尖直径不为0的楔形桩,固定桩身1/2高度处的桩径rm = 0.3 m. 图7表明桩底桩径为0时,始终无法观察到桩底反射. 桩底桩径不为0时,随桩长增加,桩底反射信号峰渐弱,当桩长L = 15 m时,几乎无法判读. 这是由于桩长的增加使得激振波能量在传递过程中受到更多桩侧土阻力的影响,损耗增加,导致信号峰降低.
图8中,桩底桩径为0时,各桩长的楔形桩表现一致,在低频区有明显的共振现象,高频区快速趋向稳定. 这是因为归一化处理后屏蔽了部分几何信息,对于大直径楔形桩,应考虑三维效应修改模型. 当桩底桩径不为0时,随着桩身长度的增加,频域响应曲线的震荡幅度减小. 这是由于在相同的激振方式下,桩土作用增强抑制了桩身振动. 同时,当桩长增加时,在低频区,同阶共振频率会发生明显的右移,在高频区,同阶共振频率逐渐恢复同步.
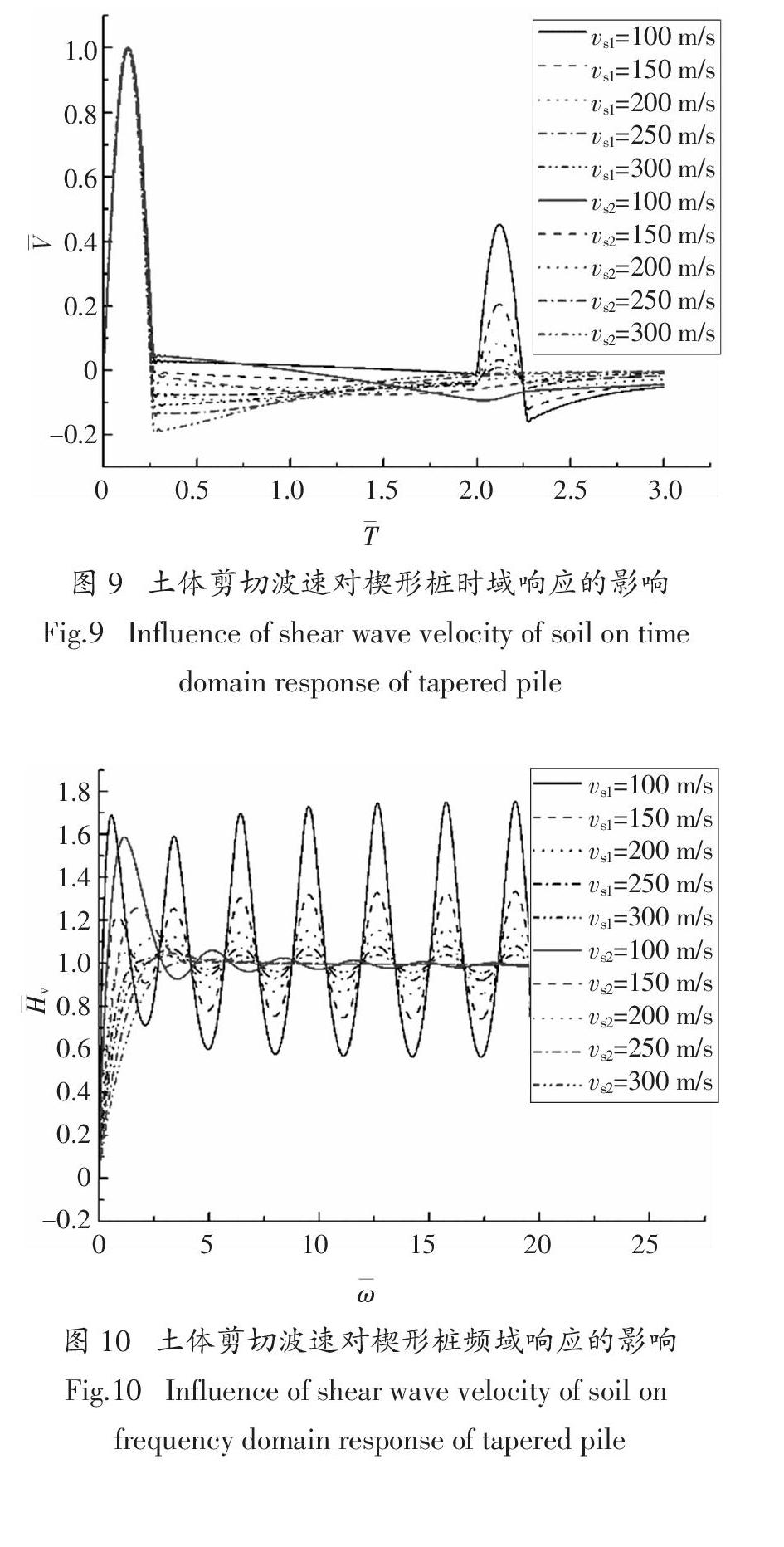
2.4 均质土体剪切波速对完整楔形桩动力响应的影响基桩嵌入地基土中工作,土体性质将会影响桩身的动力响应. 在本节中,通过改变土体的剪切波速来分析其对桩顶动力响应的影响. 基桩尺寸设置为桩长L = 10 m,楔角α = 2°.首先考虑为均质土,根据常见土质的剪切波速,设置剪切波速Vs = 100 m/s、150 m/s、200 m/s、250 m/s、300 m/s. 由图9可知,当桩底桩径为0时,没有出现桩底反射信号,对于初始激振信号之后的曲线段,土体剪切波速越大,曲线下沉越多,最终趋向一致. 在桩底桩径不为0的情况下,土体剪切波速越大,桩底反射信号峰越低,当剪切波速达到300 m/s时,桩底反射已极其微弱. 这是因为,桩土相互作用会引起与初始激振波反向的信号,在相同的楔形桩条件下,剪切波速越大,桩土相互作用越强,造成曲线下沉越多,另一方面,桩土相互作用的增大使得激振波能量损耗增加,反映在时域响应曲线上即为桩底反射峰的下降. 在图10频域响应曲线中反映出,土体的剪切波速越大,频域响应曲线的震荡幅度越小,而且在低频区域同阶共振峰的共振频率越大.当桩底桩径为0时,频域响应曲线更快地趋向稳定. 这是由于更大的桩土作用抑制了桩的纵向振动.
2.5 非均质土体剪切波速对完整楔形桩动力响应的影响
实际桩土系统中,土体的剪切波速并非均质. 因此,本节进一步考虑土体剪切波速纵向线性渐变情况下的桩体纵向振动响应. 为实现土体性质的线性渐变,将土体划分为100层,与桩体分层数一致. 控制土体剪切波速的算术平均值为150 m/s,根据桩顶土层剪切波速Vu和桩底土层剪切波速Vd的不同,分为4种变化程度考虑:①Vu = 0 m/s,Vd = 300 m/s;② Vu = 50 m/s,Vd = 250 m/s;③Vu = 100 m/s,Vd = 200 m/s;④Vu = 150 m/s,Vd = 150 m/s. 其中Case4即为均质土的情况.
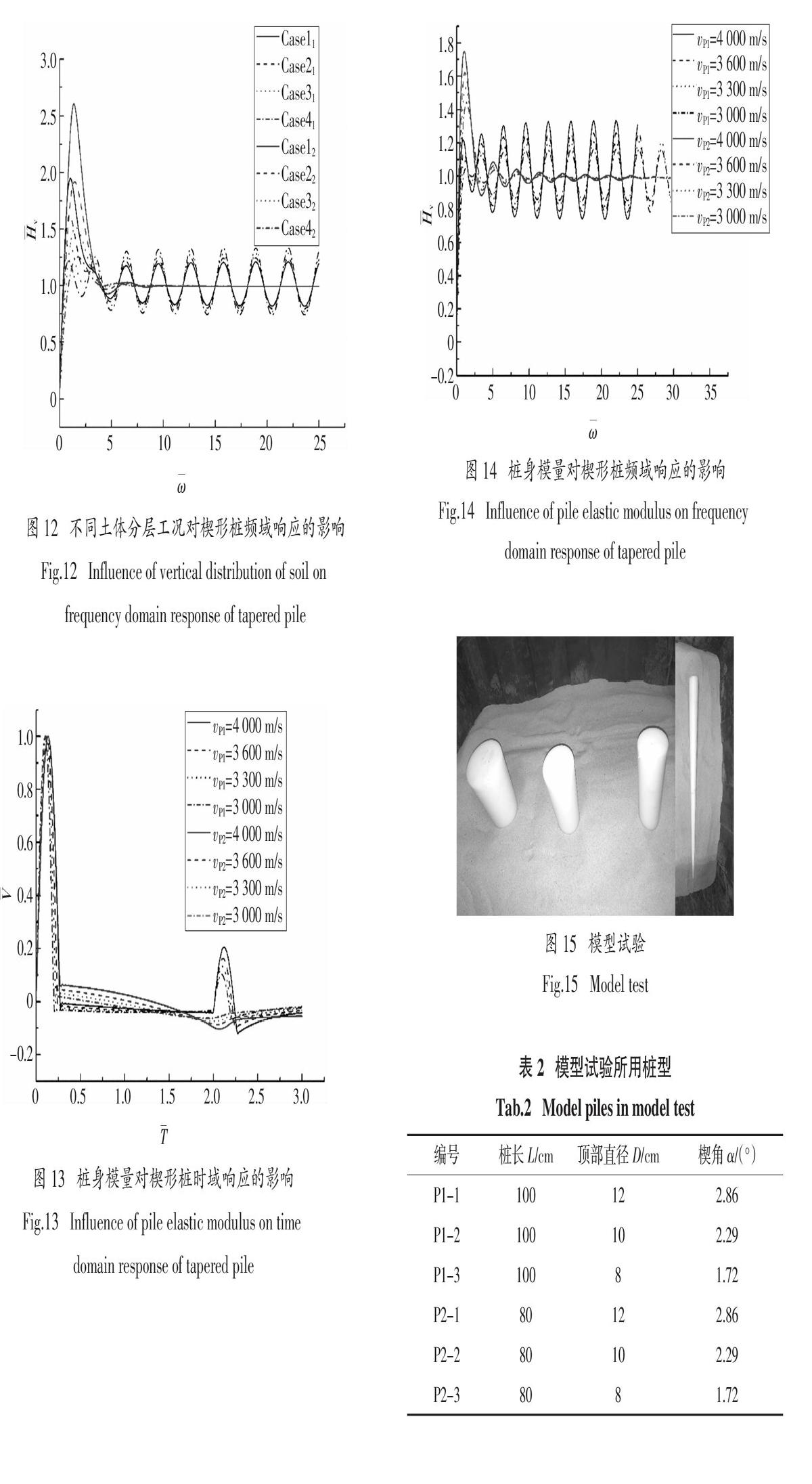
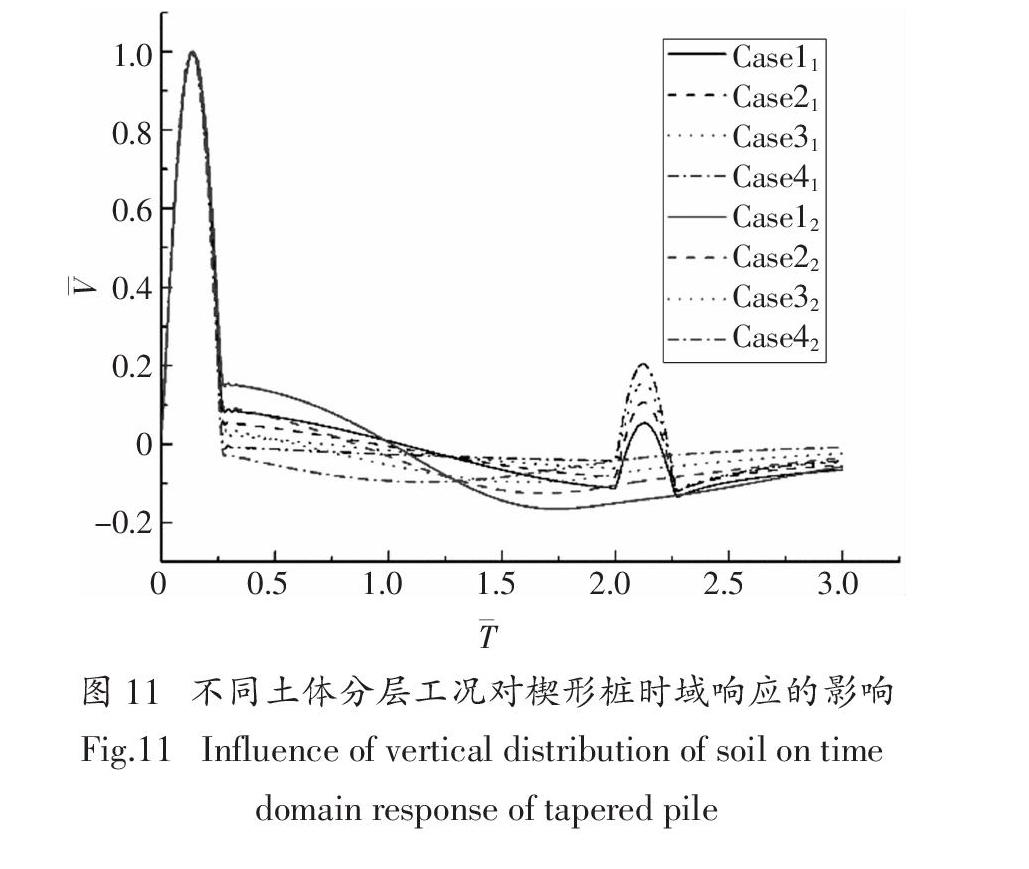
由图11时域响应曲线可知,对桩底桩径为0的楔形桩,随着土层剪切波速的差别变大,时域响应曲线的浮动也越大,但无论何种土体条件下,桩底反射信号均不可见. 桩底桩径不为0的情况下,在曲线浮动的基础上,桩底反射信号都较为明显,但会随着曲线发生竖向的平移,土层剪切波速的差别越大,下沉越多. 这是因为,上部土体剪切波速越小,桩土作用越小,曲线上抬越多,相应地,下部土体的剪切波速越大,曲线下沉越多. 另一方面,由于计算中取土体剪切波速的算术平均值相同,因此激振在传递过程中的能量损耗相差无几,所以桩底反射峰都较为明显. 图12显示,随着土层剪切波速差别增大,低频区曲线震荡幅值增大,对桩底桩径为0的楔形桩,在短暂的波动后快速趋向稳定,对桩底桩径不为0的楔形桩,同阶共振频率会右移,且高频区震荡幅度减小,同阶共振频率基本一致.
2.6 桩身纵波速对完整楔形桩动力响应的影响
事实上,桩身材料对桩顶纵向振动响应也有较大的影响. 实际工程中,由于采用不同标号的混凝土等材料,桩身弹性模量和纵波速会发生一定的变化. 考虑到常见混凝土弹性模量在30~40 GPa,纵波速控制在3 000~ 4 000 m/s的范围内进行讨论.
计算结果如图13~图14所示. 分析可知,纵波速越大,时域响应曲线上的波峰越高,对频域响应而言,曲线的震荡幅度会随之变大,共振频率几乎不发生变化. 这是由于,当桩身模量(纵波速)提高时,相同的外力作用下发生的变形会更小,相应地,桩土作用力弱化,激振波在传递过程中的损耗也更少. 在时域响应曲线上表现为波峰的增大,在频域响应曲线上表现为震荡幅度变大.
3 模型试验
为更好地验证上述楔形桩的动力响应规律,利用尼龙棒进行模型试验,如图15所示. 尼龍棒的弹性模量为4 000 MPa,密度为1 200 kg/m3,纵波传播波速约为1 800 m/s. 在模型设计中,制作桩顶直径分别为8 cm、10 cm、12 cm的模型桩,其长度均为100 cm,底部半径均为2 cm. 同时,每根模型桩都由多个桩段拼接,从而实现多种楔角多种长度的桩型模拟,具体试验参数见表2. 试验采用福建标准砂模拟桩周土,干重度14.6 kN/m3,相对密实度41%,土粒比重2.63,泊松比取0.35,剪切模量取38 MPa.
如图16、图17所示,实测曲线与理论解符合良好,且反映出相同的规律. 当桩长相同时,楔角越大,桩底反射信号越弱. 且当楔角α=2.86°时,P1-3的桩底反射信号已十分微弱,而P2-3的桩底反射仍然显著,验证了桩身越长,临界楔角越小,临界桩径比越大. 因此上述原理和方法能较好地预测楔形桩的动力响应规律,在工程实践中具有指导意义.
4 结 论
通过以上理论计算、模型试验可以得出:
1)对楔形桩引入桩径比η的概念,表示桩底部桩径d与顶部桩径D的比值,即η = d/D. 随着楔形桩的楔角增大,存在一个临界桩径比η0,使得楔形桩时域响应曲线中桩底反射信号无法显著地显示,导致对桩长、桩身完整性等信息判断不准确. 且本文研究表明,桩长越长,临界桩径比越大.
2)楔角对楔形桩的纵向振动响应有较大影响.楔角越大,时域响应曲线的上抬量越大,桩底反射信号越弱,频域响应曲线震荡幅值越小,同阶共振频率会发生不同程度的偏移,且对于桩尖直径为0的楔形桩,频域响应曲线会在短暂震荡后快速衰减为水平直线. 另一方面,桩长的增加使楔形桩的桩底反射信号渐弱,且会造成频域响应曲线的震荡幅值减小,特殊地,对桩尖直径为0的小直径楔形桩,桩长变化对纵向振动响应几乎不产生影响. 大直径楔形桩需考虑三维效应重新建模.
3)土体条件会对基桩的纵向振动响应产生较大的影响. 均质土下,土体剪切波速越大,时域响应曲线下沉越多,桩底反射信号越弱,频域响应曲线的震荡幅度越小,且在低频区同阶共振频率越大,对于桩尖直径为0的楔形桩,频域响应曲线会更快地趋向稳定. 非均质土条件下,土层剪切波速的差别越大,时域响应曲线的浮动也越大,桩底发射信号会发生纵向的平移,而其信号峰几乎不受影响. 另一方面,随着土层剪切波速的差异增大,低频区频域响应曲线的震荡幅值会变大,高频区幅值减小. 4)通过模型试验发现理论解和实测结果表现一致,验证了上述理论和方法的正确性.
参考文献
[1] 徐祖元. 锥形桩的使用经验[J]. 建筑技术,1980(2):53—55.
XU Z Y. Usage experience of taper pile [J]. Architecture Technology,1980(2):53—55. (In Chinese)
[2] KODIKARA J K,MOORE I D. Axial response of tapered piles in cohesive frictional ground [J]. Journal of Geotechnical Engineering,1993,119(4):675—693.
[3] 刘杰,何杰,闵长青. 楔形刚性桩与桩周土的非线性相互作用[J]. 铁道学报,2010,32(2):137—140.
LIU J,HE J,MIN C Q. Nonlinear interaction between the rigid taper pile and pile-surrounding soil [J]. Journal of the China Railway Society,2010,32(2):137—140. (In Chinese)
[4] NOVAK M,ABOUL-ELLA F. Impedance functions of piles in layered media [J]. Journal of the Engineering Mechanics Division,1978,104(3):643—661.
[5] GOUGH W,RICHARDS J P G,WILLIAMS R P,et al. Vibrations and waves [J]. Physics Today,1996,49(12):53—54.
[6] KOTEN H V,MIDDENDORP P,BREDERODE P V. An analysis of dissipative wave propagation in a pile [C]//Proceedings of International Seminar on the Application of Stress Wave Theory on Piles. Stockholm,1980:22—40.
[7] 郭平. 敲击法测桩的波动原理[J]. 湖南大学学报(自然科学版),1992,19(4):82—88.
GUO P. The wave-theoretical principle of the impact method of testing piles [J]. Journal of Hunan University (Natural Sciences),1992,19(4):82—88. (In Chinese)
[8] 王奎华,谢康和,曾国熙. 变截面阻抗樁受迫振动问题解析解及应用[J]. 土木工程学报,1998,31(6):56—67.
WANG K H,XIE K H,ZENG G X. An analytical solution to forced vibration of foundation pile with variable section impedance and its application [J]. China Civil Engineering Journal,1998,31(6):56—67. (In Chinese)
[9] 王奎华,张宏志,李振亚,等. 桩底土对既有承台单桩纵向振动特性的影响研究[J]. 湖南大学学报(自然科学版),2017,44(11):170—176.
WANG K H,ZHANG H Z,LI Z Y,et al. Study on influence of pile subsoil on vertical vibration characteristic of single pile with cushion cap [J]. Journal of Hunan University (Natural Sciences),2017,44(11):170—176. (In Chinese)
[10] 王奎华,高柳,肖 ,等. 考虑桩周土竖向作用大直径楔形桩纵向振动特性[J]. 岩土力学,2016,37(S2):223—231.
WANG K H,GAO L,XIAO S,et al. Dynamic characteristic of large diameter tapered pile considering vertical reaction of pile surrounding soil [J]. Rock and Soil Mechanics,2016,37(S2):223—231. (In Chinese)
[11] 陈安国,刘东甲. 基桩低应变检测的波动方程法数值计算[J]. 合肥工业大学学报(自然科学版),2007,30(10):1336—1340.
CHEN A G,LIU D J. Numerical computation of the wave equation for low strain test piles [J]. Journal of Hefei University of Technology(Natural Science),2007,30(10):1336—1340. (In Chinese)
[12] 吴文兵,王奎华,武登辉,等. 考虑横向惯性效应时楔形桩纵向振动阻抗研究[J]. 岩石力学与工程学报,2011,30(S2):3618—3625.
WU W B,WANG K H,WU D H,et al. Study of dynamic longitudinal impedance of tapered pile considering lateral inertial effect [J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(S2):3618—3625. (In Chinese)
[13] 吴文兵,王奎华,窦斌. 任意层地基中粘弹性楔形桩纵向振动响应研究[J]. 振动与冲击,2013,32(8):120—127.
WU W B,WANG K H,DOU B. Vertical dynamic response of a viscoelastic tapered pile embedded in layered foundation [J]. Journal of Vibration and Shock,2013,32(8):120—127. (In Chinese)
[14] 吴文兵,谢帮华,黄生根,等. 考虑挤土效应时楔形桩纵向振动阻抗研究[J]. 地震工程学报,2015,37(4):1042—1048.
WU W B,XIE B H,HUANG S G,et al. Vertical dynamic impedance of tapered piles considering compacting effects [J]. China Earthquake Engineering Journal,2015,37(4):1042—1048. (In Chinese)
[15] 张献民,蔡靖,王建华. 基桩缺陷逐步能量恢复递推定量分析
[J]. 岩土力学,2003,24(S2):481—484.
ZHANG X M,CAI J,WANG J H. Quantitative recurrence analysis to determine defects of piles by energy recovery method [J]. Rock and Soil Mechanics,2003,24(S2):481—484. (In Chinese)
收稿日期:2018-05-05
基金项目:国家自然科学基金资助项目(51779217),National Natural Science Foundation of China(51779217)
作者简介:王奎华(1982—),男,江苏滨海人,浙江大学教授,博士生导师
通讯联系人,E-mail:zdwkh0618@zju.edu.cn

