基于贝叶斯傅里叶动态模型的桥梁极值应力预测

樊学平 屈广 刘月飞

摘   要：研究了基于健康监测应力数据的桥梁极值应力动态预测.考虑到监测应力的周期性、随机性和动态性等特点，首先初次建立了桥梁监测极值应力的傅里叶动态非线性模型（Fourier Dynamic Nonlinear Model，FDNM），结合Taylor级数展开技术，将FDNM近似转化为傅里叶动态线性模型（Fourier Dynamic Linear Model，FDLM）;然后采用贝叶斯方法，基于动态监测极值应力数据，建立了无先验信息的贝叶斯傅里叶动态线性模型（Bayesian Fourier Dynamic Linear Model： BFDLM），进而对监测极值应力的一步向前预测分布参数和后验应力状态分布参数进行了预测分析;最后通过实际桥梁监测极值应力数据对本文所建模型和方法的合理性及适用性进行了验证分析，结果表明本文所建BFDLM能够反映桥梁极值应力的周期性、随机性以及动态性等特点.研究成果将为桥梁监测极值应力预测提供理论基础和应用方法.

关键词：桥梁;傅里叶动态非线性模型;Taylor级数展开技术;贝叶斯方法;桥梁极值应力预测

中图分类号：TU391; TU392.5                  文献标志码：A

Abstract： The dynamic prediction of bridge extreme stress based on health monitoring stress data was studied. Considering the monitored stresses periodicity， randomness， dynamic characteristics and so forth，firstly，the Fourier Dynamic Nonlinear Model（FDNM） of bridge monitored extreme stress was built，and， with Taylor series expansion technology， FDNM was approximately transferred into the Fourier Dynamic Linear Model（FDLM）;secondly， with Bayes method， the Bayesian FDLM（BFDLM） was built based on the monitored extreme stress data，and the one-step forward prediction distribution parameters of monitored extreme stress and distribution parameters of posterior stress state were dynamically predicted; finally， the monitored extreme stress data of an actual bridge was provided to illustrate the application and feasibility of the proposed models and methods. The results show that the proposed BFDLM can reflect bridge extreme stresses' periodicity， randomness， dynamics and so forth，which can provide the theoretical foundation and application approach for bridge monitoring extreme stress prediction.

Key words： bridge;Fourier dynamic nonlinear model;Taylor series expansion technology;Bayesian approach; bridge extreme stress prediction

橋梁健康监测系统在长期运营中积累了大量监测数据，如应力、应变、挠度、加速度等.发展至今，监测数据合理应用的研究主要集中在模态分析[1]、损伤识别与评估[1-2]、模型修正[3]以及可靠性评估[4-5]等领域，仍难以有效预测结构的动态可靠性，因此如何有效利用监测信息预测结构可靠性仍是桥梁健康监测领域备受关注的研究难点.而结构可靠性主要跟抗力与荷载效应相关，因而合理动态预测荷载效应就成为结构可靠性预测的关键问题.

考虑到桥梁有限元建模和模型更新的复杂性和困难性，采用无需模型的分析方法逐渐成为桥梁健康监测领域的研究趋势.基于实际监测数据，采用无需模型的分析方法预测桥梁的荷载效应已取得一些研究成果，但多为基于离线监测信息的预测研究[5-7]，而基于实时监测信息的动态预测研究相对较少，且研究成果存在一定的局限性，如：Frangopol等[8-9]提出了基于监测极值一次回归函数的桥梁性能的可靠性预测方法，并于同年提出了基于贝叶斯更新的桥梁可靠性预测方法，两种方法分析过程中分别采用一次回归函数和常值函数进行荷载效应动态预测，均未考虑监测变量的动态随机性和周期性;赵卓[10]采用ARMA模型动态预测了长春伊通河桥构件的荷载效应（挠度、加速度以及索力等），分析过程中亦未考虑监测变量的动态随机性和周期性，且存在模型长期预测精度不高的问题;樊学平等[11-13]利用监测数据，研究了基于贝叶斯动态线性模型和贝叶斯动态非线性模型的桥梁构件可靠性动态预测方法，分析过程中存在以下两个问题：a）荷载效应的动态预测均未考虑监测变量数据周期性的特点，即贝叶斯动态模型的状态方程均未考虑监测变量状态的周期性;b）动态模型中监测误差的方差均为已知.综上所述，本文作者经过研究发现，存在以下问题需要解决：1）如何建立考虑监测数据动态性、随机性以及周期性等特点的动态模型;2）在监测误差未知的情况下，如何采用贝叶斯方法对动态模型进行概率递推.

鉴于上述问题，本文通过傅里叶函数来建立先验信息未知的桥梁监测极值应力动态模型，采用贝叶斯方法对其进行概率递推，实现桥梁极值应力的动态预测.

1   研究流程及步骤考虑到监测数据的动态性、随机性以及周期性，本文所提的桥梁极值应力动态预测的详细流程图如图1所示.

结合图1可得具体研究步骤为：1）利用桥梁系统历史监测极值应力数据，本文认为其为一个时间序列，对其进行五点三次平滑处理，近似得到极值应力状态数据，采用傅里叶函数和Taylor级数展开技术，近似得到极值应力的线性状态方程，并将状态方程与历史监测极值应力数据相结合得到线性监测方程，进而可得桥梁极值应力无先验信息的傅里叶动态线性模型（FDLM）;2）基于建立的无先验信息FDLM和动态监测极值应力数据，采用贝叶斯方法，实现桥梁极值应力的动态概率预测，并通过实际桥梁的监测极值应力数据验证所提方法的合理性和适用性.

2   桥梁监测极值应力无先验信息的FDLM傅里叶动态线性模型（FDLM）由线性监测方程、基于傅里叶函数和Taylor级数展开技术的线性状态方程以及初始状态信息三部分组成.状态方程反映了监测变量和系统随时间变化的水平，监测方程反映了监测变量和状态变量之间的关系.本文所建立的FDLM基于两点假设[14-15]：

1）状态变量{θt}的变化是一个马尔科夫过程;

2）监测变量{yt}相互独立，且只与状态变量相关.

2.1   状态方程的建立本文主要通过桥梁历史监测极值应力数据建立动态线性模型，其中状态方程的详细建立步骤

如下：

1）利用五点三次平滑处理方法[10]，对桥梁历史监测极值应力数据进行重采样，近似得到初始极值应力状态数据;

2）采用傅里叶函数（反映数据的周期性）对初始应力状态数据进行回归分析，得到极值应力状态的回归函数;

3）利用回归函数，结合Taylor级数展开技术，建立傅里叶线性状态方程.初始极值应力状态的回归函数为

4   实桥应力预测分析（天津富民桥）

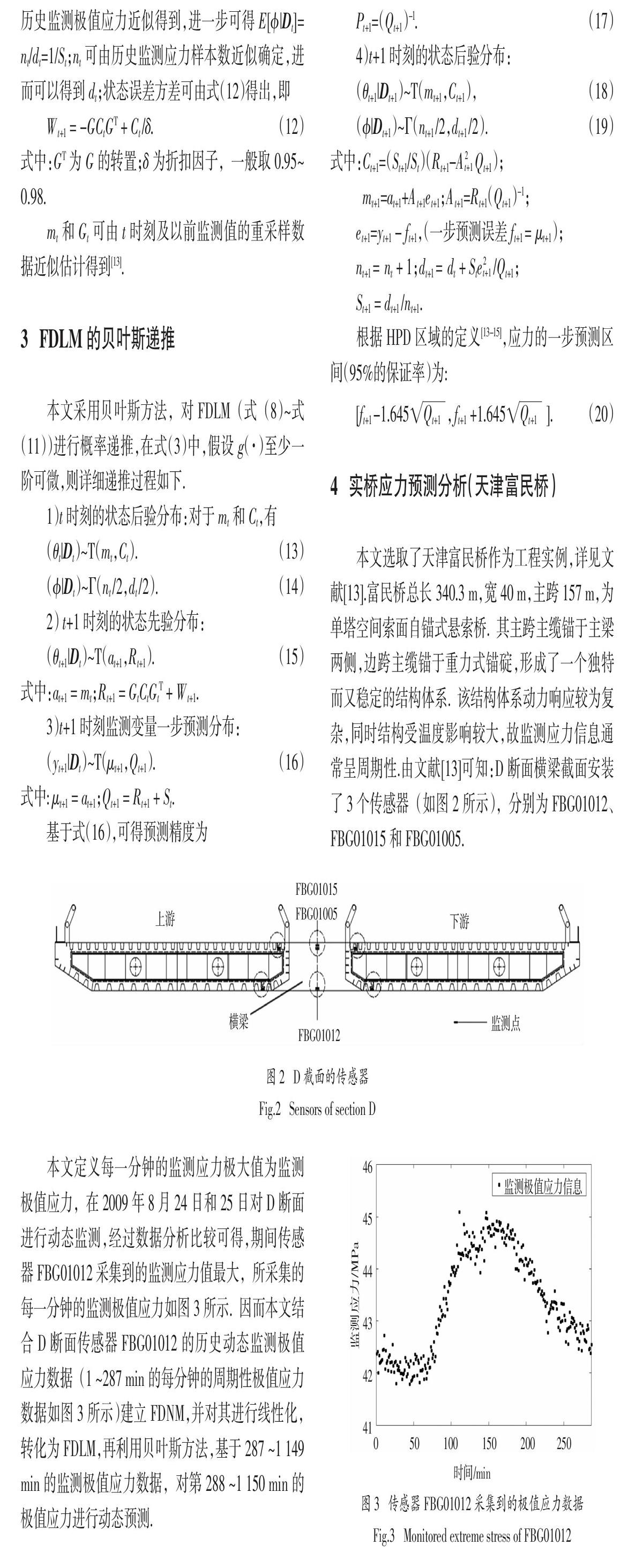
本文选取了天津富民桥作为工程实例，详见文献[13].富民桥总长340.3 m，宽40 m，主跨157 m，为单塔空间索面自锚式悬索桥.其主跨主缆锚于主梁两侧，边跨主缆锚于重力式锚碇，形成了一个独特而又稳定的结构体系.该结构体系动力响应较为复杂，同时结构受温度影响较大，故监测应力信息通常呈周期性.由文献[13]可知：D断面横梁截面安装了3个传感器（如图2所示），分别为FBG01012、FBG01015和FBG01005.

本文定义每一分钟的监测应力极大值为监测极值应力，在2009年8月24日和25日对D断面进行动态监测，经过数据分析比较可得，期间传感器FBG01012采集到的监测应力值最大，所采集的每一分钟的监测极值应力如图3所示.因而本文结合D断面传感器FBG01012的历史动态监测极值应力数据（1 ～287 min的每分钟的周期性极值应力数据如图3所示）建立FDNM，并对其进行线性化，转化为FDLM，再利用贝叶斯方法，基于287 ～1 149 min的监测极值应力数据，对第288 ～1 150 min的极值应力进行动态预测.

式中：yt为t时刻的监测应力值;vt为监测误差;V为常值未知方差，可以通过St-1 = dt-1 /nt-1近似估计.mt-1 和Ct-1可以通过前287 min应力数据经过五点三次平滑处理的数据（平滑处理后的初始信息见图4）近似估计得到.

采用式（8）～式（20）和式（22）～式（25），利用1～287 min的监测应力数据建立的FDLM，对第288～574 min（后287 min）的应力进行动态预测，结果如图5～图7所示.

由图5与图6可知，预测应力与监测应力的大小近似相等，且预测应力区间均包含了监测应力和预测应力的所有数据，证明了本文所建模型是合理的.

由图7可知，由式（17）计算得到的FDLM的预测精度随着监测应力的不断修正越来越好，进一步验证了本文所建模型的合理性.

5   结   论

本文考虑到桥梁监测信号的随机性、动态性以及周期性等特点，首次建立了傅里叶动态线性模型，采用贝叶斯方法对其进行了动态概率递推，并利用实际桥梁监测数据对其进行了验证分析，结论如下：

1）无先验信息FDLM能够对桥梁极值应力进行合理的预测，预测值和监测值的变化趋势一致，大小近似相等，而且能够有效反映实时监测数据的变化范围和趋势，并且由于模型方差未知，更为符合工程实际.

2）无先验信息FDLM随着实时监测数据的不断修正，预测精度越来越高.说明预测的客观性越来越好.这些成果将为桥梁健康监测提供一定的理论基础.

参考文献

[1]    李顺龙. 基于健康监测技术的桥梁结构状态评估和预警方法研究[D]. 哈尔滨： 哈尔滨工业大学土木工程学院，2009：18—39.

LI S L. Approached of condition assessment and damage alarming of bridges based on structural health monitoring[D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2009：18—39. （In Chinese）

[2]    宗周紅，钟儒勉，郑沛娟，等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报，2014，27（12）：46—57.

ZONG Z H，ZHONG R M，ZHENG P J，et al. Damage and safety prognosis of bridge structures based on structural health monitoring：progress and challenges [J]. China Journal of Highway and Transport，2014，27（12）：46—57. （In Chinese）

[3]    魏锦辉，任伟新. 基于响应面方法的桥梁静动力有限元模型修正[J]. 公路交通科技，2015，32（2）：68—73.

WEI J H，REN W X. Static and dynamic bridge finite element model updating based on response surface method [J]. Journal of Highway and Transportation Research and Development，2015，32（2）：68—73. （In Chinese）

[4]    焦美菊，孙利民，李清富. 基于监测数据的桥梁结构可靠度评估[J]. 同济大学学报（自然科学版），2011，39（10）：1452—1457.

JIAO M J，SUN L M，LI Q F. Bridge structural reliability assessment based on health monitoring data [J]. Journal of Tongji University （Natural Science）， 2011， 39（10）： 1452—1457.  （In Chinese）

[5]  FRANGOPOL D M，STRAUSS A，KIM S. Bridge reliability assessment based on monitoring [J]. Journal of Bridge Engineering，2008，13（3）：258—270.

[6]    WALSH S B，BORELLO D J，GULDUR B，et al. Data processing of point clouds for object detection for structural engineering applications [J]. Computer-Aided Civil and Infrastructure Engineering，2013，28（7）：495—508.

[7]    CATBAS F N，SUSOY M，FRANGOPOL D M. Structural health monitoring and reliability estimation：long span truss bridge application with environmental monitoring data [J]. Engineering Structures，2008，30（9）：2347—2359.

[8]    FRANGOPOL D M，STRAUSS A，KIM S Y. Use of monitoring extreme data for the performance prediction of structures：general approach [J]. Engineering Structures，2008，30：3644—3653.

[9]    STRAUSS A，FRANGOPOL D M，Kim S Y. Use of monitoring extreme data for the performance prediction of structures：Bayesian updating [J]. Engineering Structures，2008，30：3654—3666.

[10]  赵卓. 基于ARMA模型的伊通河桥监测数据建模与可靠度分析[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2012：35—93.

ZHAO Z. Health monitoring data modeling and reliability analysis for Yitong river bridge based on ARMA model [D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2012：35—93. （In Chinese）

[11]  L？譈 D G，FAN X P. Bayesian forecasting of structural bending capacity of aging bridges based on dynamic linear model [J]. Journal of Harbin Institute of Technology，2012，44（12）：13—17.

[12]  樊学平，吕大刚. 基于多个BDLM的桥梁结构可靠度实时预测[J]. 华南理工大学学报（自然科学版），2013，41（3）：70—75.

FAN X P，L？譈 D G. Real-time reliability forecast of bridge structures based on multiple BDLMs [J]. Journal of South China University of Technology，2013，41（3）：70—75. （In Chinese）

[13]  樊学平. 基于验证荷载和监测数据的桥梁可靠性修正与贝叶斯预测[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2014：39—84 .

FAN X P. Bridge reliability updating and Bayesian prediction based on proof loads and monitored data [D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2014：39—84. （In Chinese）

[14]  WEST M，HARRISON J. Bayesian forecasting and dynamic models [M]. 2nd ed. New York：Springer Series，1997：32—37.

[15]  PETRIS G，PETRONE S，CAMPAGNOLI P. Dynamic linear models with R[M]. New York：Springer Series，2009：31—84.

收稿日期：2018-05-16

基金项目：国家自然科学基金资助项目（51608243），National Natural Science Foundation of China（51608243）;甘肃省自然科学基金资助项目（1606RJYA246），Natural Science Foundation of Gansu Province（1606RJYA246）

作者簡介：樊学平（1983—），男，山西运城人，兰州大学副教授，博士

通讯联系人，E-mail：fxp_2004@163.com