基于教材例、习题的题组设计与思考

张合远

（浙江省平阳县教师发展中心）

现行浙教版《义务教育教科书·数学》（以下统称“教材”）中为我们提供了丰富的例、习题，但在许多情况下，对于过于直白的问题、相对简约的过程，如果只是一味地“拿来主义”，学生获得的往往只是知识经验的简单叠加，而对数学思维、创新意识与实践能力等深层目标则很难企及.因此，教师在吃透教材本意的基础上，有必要对教材例、习题进行合理的加工.而题组设计正是大多数教师惯用的策略之一，它不仅有利于学生在原有的认知基础上进行新知建构，而且有利于学生在比较中探究新知.本文通过教材例、习题教学中的几个具体案例，结合自己的教学实践，辅图诠释教学设计，就如何依据教材例、习题，合理地串题、科学地变题和大胆地挖题，在题组思辨中提高学生的思维层次，谈几点做法，以期与同仁探讨.

一、合理串题，聚焦式夯实“四基”，引发思维深度发展

所谓聚焦式，如图1，即选用的教材例、习题集中反映某一个基本定理或者某一个基本图形，从而让学生在解决不同问题的基础上，夯实基础知识、基本技能、基本思想和基本活动经验，落实对几何基本图形的综合运用.

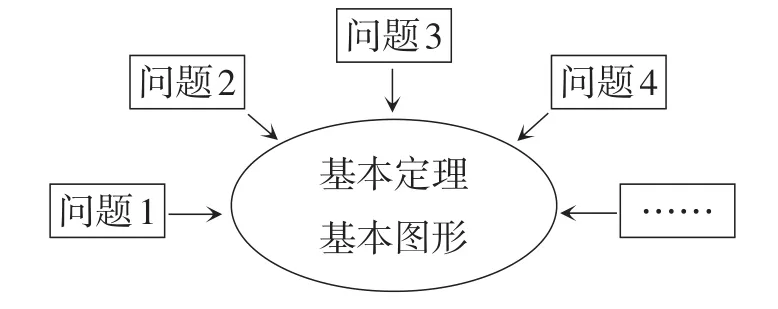
图1

1.聚焦基本定理，促进学生对定理的深度理解

案例1：在学习了教材八年级下册“平行四边形的判定定理”（第1课时）后，学生能否深刻理解一组对边平行并且相等的四边形是平行四边形，并熟练使用该定理解决问题是非常重要的.为了实现这一教学目标，我们可以考虑仿照图2，重组教材例、习题的呈现顺序，并合理组织教学.

图2

题目1如图3，已知在ABCD中，E，F分别是AB，CD的中点.求证：EF∥AD∥BC.

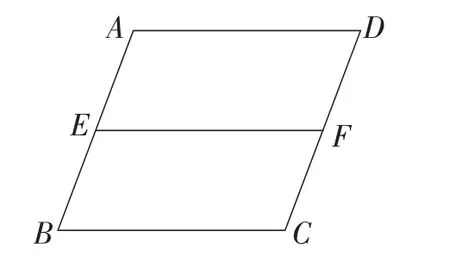
图3

题目2如图4，E，F分别是ABCD边AD，BC的中点.求证：BE=DF.

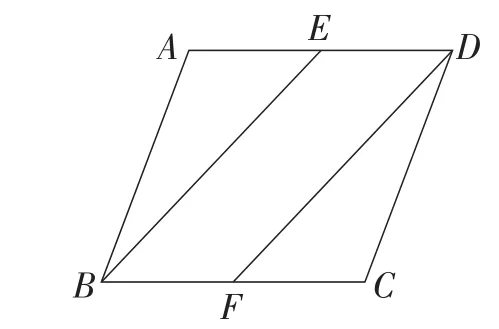
图4

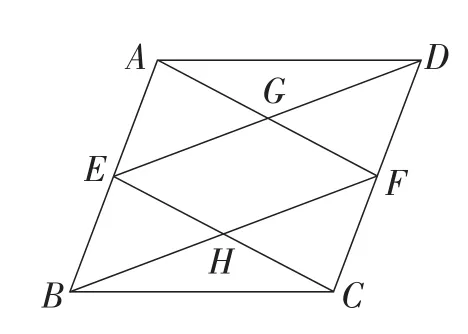
图5

题目3如图5，在ABCD的一组对边上取AE=CF，问图中有几个平行四边形，并证明.

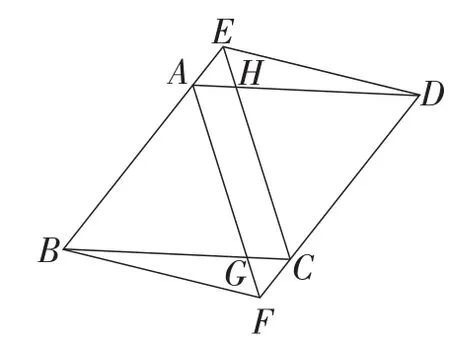
图6

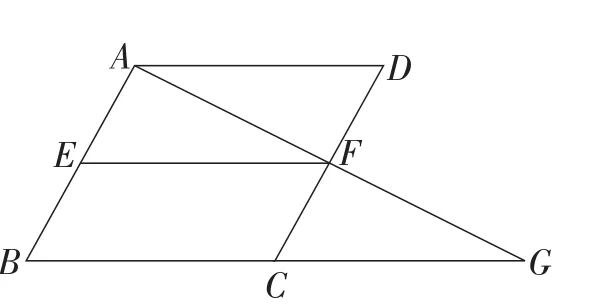
图7

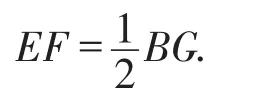
【设计说明】以上题目中，题目1与题目2都是平行四边形性质与判定的简单应用，属于水平变式.但是题目1的图形是标准图式，学生容易识别，题目2的图式是非标准图式，会对学生的判断造成一定的干扰；题目3及其变式显然是题目2的叠加，需要学生具有在复杂图形下分离出基本图形的能力，对学生的思维能力提出了更高的要求；题目4需要把三角形的问题转化成平行四边形的问题来处理，属于垂直变式，提高了学生灵活运用知识的能力.

例、习题是教材的重要组成部分，其存在的意义不言而喻，不要将看似简单的教材例、习题一笔带过，甚至无暇顾及.教师要对教材例、习题进行全方位反思.在教学中，要把初中数学内容视作一个整体，从整体性和全局性的角度进行教材例、习题教学，这样才能活化教材例、习题，从而更大限度发挥教材例、习题的价值和功能.

2.聚焦基本图形，促进学生几何思维拾级而上

我们知道，许多数学问题都可以化归为一个已经熟悉的“元问题”来解决.但由于教师与学生知识量上的差异，导致教师眼中的“元”未必就是学生所认同的“根”.因此，利用教材编制题组而使“元问题”逐步呈现是非常重要的.同时，为了激活不同思维程度学生几何思维能力的发展，教师要尽可能设计不同思维层次的题组，让不同层次的学生通过积极思考更上一个思维台阶.

案例2：教材九年级上册“垂径定理”（复习课）题组设计.

对于垂径定理及其逆定理而言，无论是初学还是提升，都指向一个基本图形（由弦心距、弦的一半、半径所组成的直角三角形），所以此问题就自然成为本节复习课的“元问题”.

题目1如图8，⊙O中弦AB的长为8，弦AB的弦心距为3，求⊙O的半径.

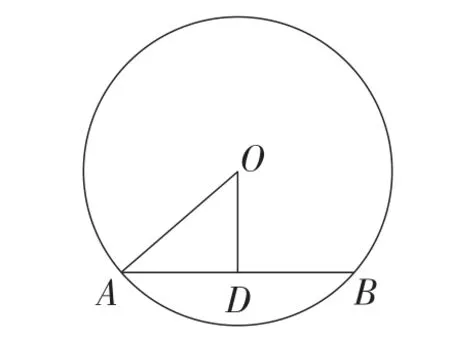
图8

题目2如图9，AB是⊙O的弦，AB=8 cm，半径OC⊥AB，垂足为点D，CD=2 cm，求⊙O的半径.

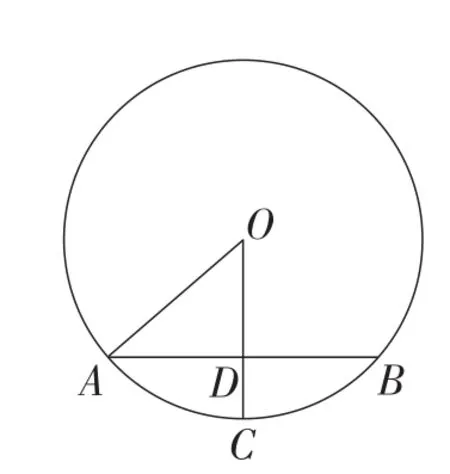
图9

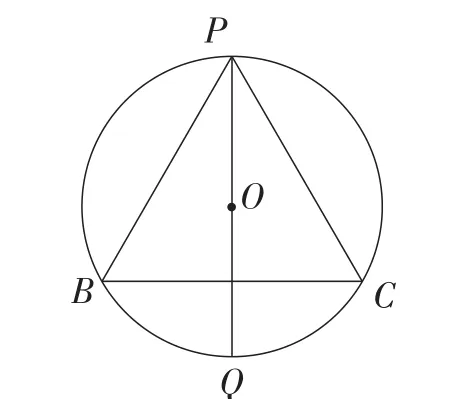
图10

题目3如图10，⊙O的半径为1，PQ是⊙O的直径，△PBC是⊙O内接等边三角形，求△PBC的边长.

题目4如图11，⊙O的半径为1，PQ是⊙O的直径，两个全等的等边三角形都关于PQ对称，其中，△A1B1C1的顶点A1与点P重合，△A2B2C2的顶点A2是B1C1与PQ的交点，其余两个顶点B2，C2都在圆上.

（1）求此时等边三角形的边长a2；

（2）如图12，若有n个相同的等边三角形按此方式排列，求此时等边三角形的边长an（用含n的代数式表示）.

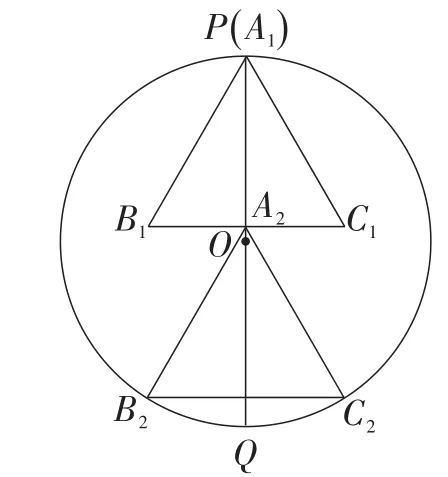
图11

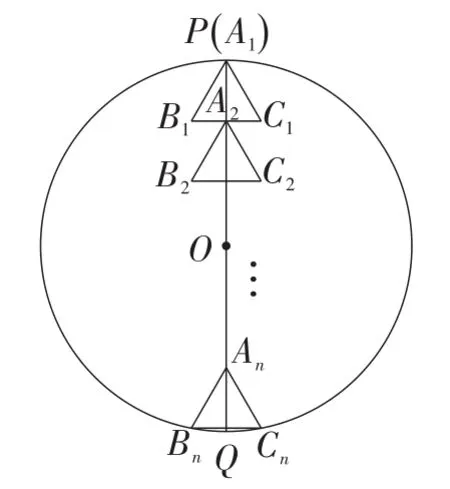
图12

【设计说明】由垂径定理的相关基本问题（基本图形）出发，直接应用垂径定理和勾股定理求半径，再应用垂径定理、勾股定理和方程思想求半径，有利于学生对基本问题本质的理解，有利于培养学生的思维能力.而后将基本问题进行两次拓展：一是添加辅助线由半径求弦长；二是由一个等边三角形变为2个或n个等边三角形，从特殊到一般，虽然等边三角形的数量发生了变化，但是其中蕴含着不变的解题策略，有助于学生深刻理解问题本质和学生几何思维能力的发展.

一道典型的教材例、习题，不但能深化教学内容以此固本，而且还能抛砖引玉以此拓新.从信息加工心理学对知觉的研究主要涉及模式识别来分析，整体的结构在模式识别中能够起到很好的作用，这种现象被心理学家称为“结构优势效应”，这种效应与人的知觉组织是有密切关系的.因此，一旦学生掌握了基本图形的特点，就能够在复杂的图形中快速地识别或构造出基本图形，从而实现数学方法的有效迁移，进而提高思维能力.

二、科学变题，发散式多向思考，促进思维广度发展

所谓发散式，即围绕教材中某道典型的例、习题，通过变换特殊数据、条件或结论，转换问题的形式或内容，可以从数量关系和数学运算出发，也可以从问题的结构特征出发进行多角度的变式题组设计，激发学生发散式思考（如图13）.学生在分析、解决变式题组的过程中，经历观察、分析、抽象等思维活动，让学生体验数学的价值和魅力，激活其思维原动力，进而发展其综合思维能力.

图13

案例3：特殊三角形与方程、函数相关的综合问题非常多，所涉及到的解题策略、数学思想方法也非常丰富.在设计变式题组和组织课堂教学时，我们可以仿照如图14所示的模式，精选教材例、习题进行变式题组教学，也可以从一个问题出发，自然生长出不同的问题情境进行多角度思考，促进思维广度的发展.

图14

题目如图15，△ABC是等边三角形，D，E，F分别是各边上的一点，且AD=BE=CF，则△DEF是等边三角形.试说明理由.

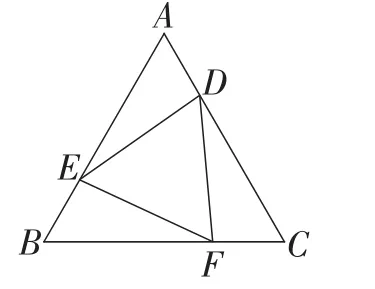
图15

我们可以将D，E，F三点都改为动点，即将静态问题改编为动态问题.

变式1：如图15，等边三角形ABC的边长为4 cm，点D，E，F分别从点A，B，C同时出发，以1 cm/s的速度沿着等边三角形的边向点B，C，A运动.设运动时间为t（s）.

（1）求证：△DEF是等边三角形；

（2）当t为何值时，△DEF的面积为 3cm？

解析：（1）由已知易得AE=BF=CD，CF=BE=AD，∠A=∠B=∠C=60°.所以△ADE≌△BEF≌△CDF.

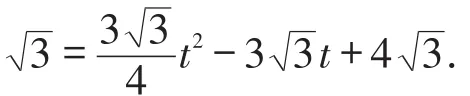
在中考复习时，第（2）小题也可以改编成与函数有关的问题.例如，设△DEF的面积为S(c m2)，求S关于t的函数表达式和自变量t的取值范围.

若改变点的连接方式，则又可以得到以下变式题.

变式2：如图16，等边三角形ABC的边长为4 cm，点E，F，D分别从点A，B，C同时出发，以1 cm/s的速度沿着等边三角形ABC的边向点B，C，A运动.设运动时间为t（s）.

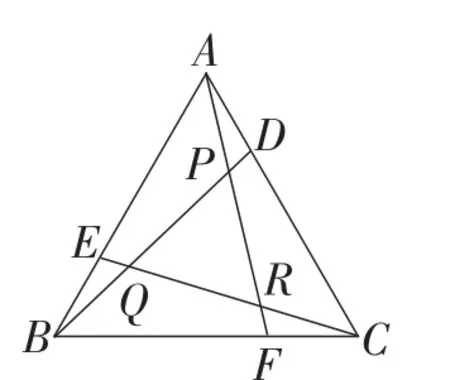
图16

（1）求证：△PQR是等边三角形；

（2）设△PQR的面积为S(c m2)，求S关于t的函数表达式和自变量t的取值范围.

若改变点在等边三角形边上运动为在边的延长线上运动，则又可得以下变式题.

变式3：如图17，点E，F，D分别从等边三角形ABC上的点A，B，C同时出发，以相同的速度分别沿着射线AB，BC，CA运动.

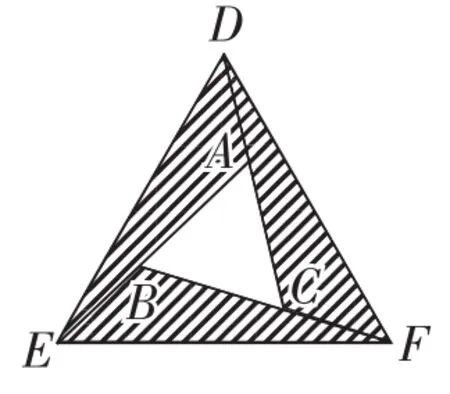
图17

（1）求证：△DEF是等边三角形；

（2） △BEF的周长为 30，设BE=a，BF=b，EF=c，若a+b=c+2，求图17中阴影部分的面积．

上述改编后的问题是同时、同速的质点运动问题，为了促进学生思维广度的发展，我们还可以将它改编为以下的同时、异速的动态问题．

变式4：如图18，等边三角形ABC的边长为4 cm，点E，F，D分别从点A，B，C同时出发，分别以1 cm/s，3 cm/s，4 cm/s的速度沿着等边三角形的边向点B，C，A运动.设运动时间为t（s），则当t为何值时，∠EFD=60°？

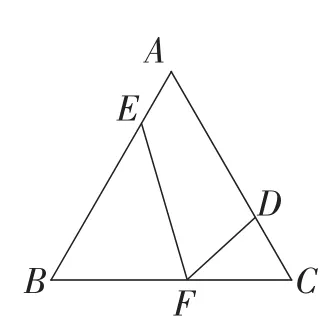
图18

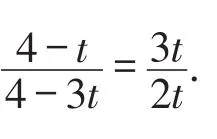
若将等边三角形ABC放到平面直角坐标系中，把三个点运动改为两个点运动，则又可以得到以下改编题.

变式5：如图19，在平面直角坐标系中，O是坐标原点，∠OCP=60°，点A为线段PC的中点，点C的坐标为(4，0).一动点F在线段OC上以每秒1个单位的速度由点O向终点C运动，同时，点D在线段CA上由点C向终点A运动.设点D的运动速度为每秒x个单位，它们运动的时间为t秒.

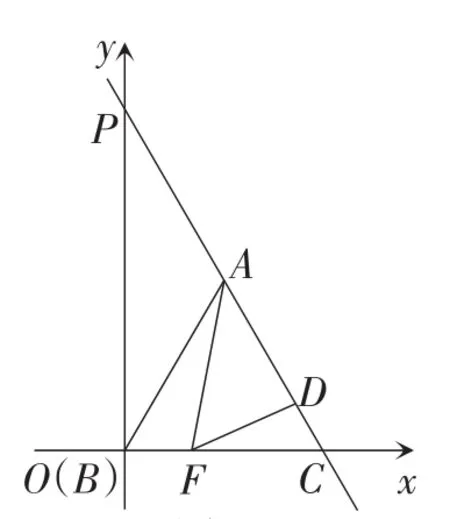
图19

（1）求直线PC的函数表达式及点A的坐标.

（2）在运动过程中，设△ADF的面积为S.

①求S关于t的函数表达式.

②是否存在实数x，使得△AOF与△FCD相似？若存在，试求出相应的S与x的值；若不存在，试说明理由.

（3）若∠CDF=90°，点D关于AF的对称点D′落在△AOF的内部（不包括边）时，则x的取值范围为 .

我们还可以将等边三角形改为平行四边形、矩形、菱形和正方形等.当学生熟悉了这样的题组呈现方式后，就会逐渐明晰动态问题并不可怕，只要将它们静态化处理，问题就会迎刃而解.

【设计说明】以上变式题组的设计，从图形的呈现方式上，突出了从静止到运动、从简单到复杂的基本思路；从知识运用上分析，强化了从全等到相似、从方程到函数的转变；从思想方法层面的体验上，让学生经历了从特殊到一般的过程.由此，学生对数学基础知识和思想方法经历了从肤浅到深刻的认识、从零散到系统的把握，从而学会思考和辨析，学会以不变应万变，进一步提升了思维的广阔性.

三、大胆挖题，拓展式探究学习，引领思维创新发展

所谓拓展式，即我们对教材中某道具体的例、习题，通过观察猜想、由表及里、深入思考、合作探究，挖掘出隐含在其中的一般性结论，给出严谨的推导证明，并加以推广应用（如图20）.

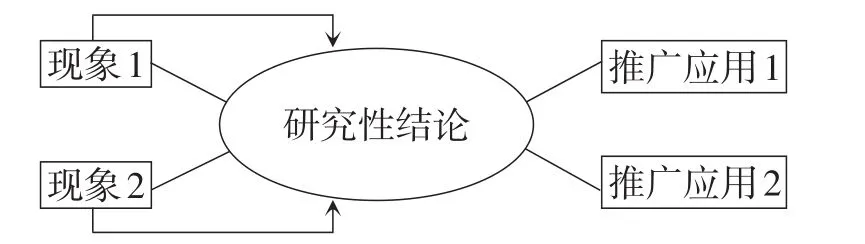
图20

案例4：从一道习题到一类函数研究性问题的探究.

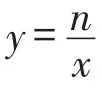
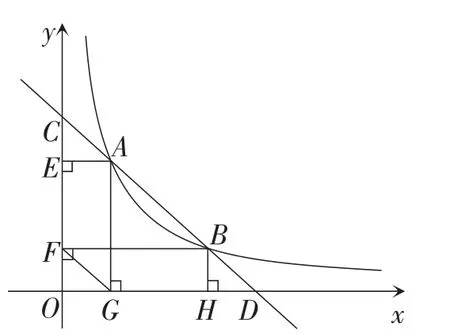
图21

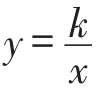
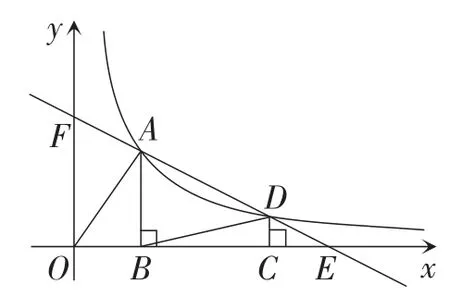
图22

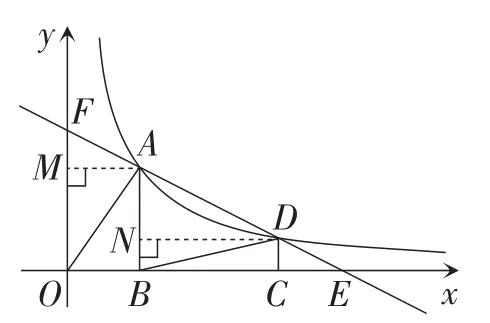
图23

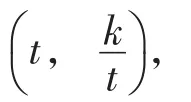
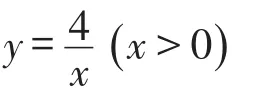
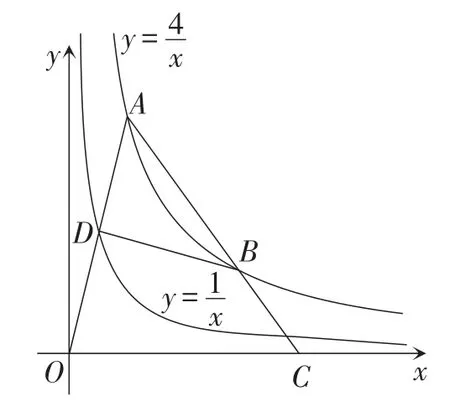
图24

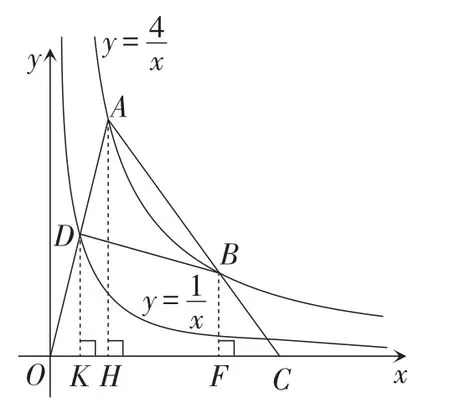
图25

解析：如图25，分别过点D，A，B作垂直于x轴的线段，垂足分别为点K，H，F，结合基本结论可知，OH=CF.

因为AB∶BC=2∶1，

所以HF∶CF=2∶1.

因为S△DOK∶S△AOH=1∶4，

所以OK∶OH=1∶2.

不妨设OK=t，则OH=CF=2t，OF=6t.

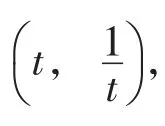
【设计说明】上述案例通过对一道普通习题进行深入思考，发现几个结论，于是鼓励学生大胆猜想、仔细求证，从而得出几个一般性的结论，之后给出相应的推广应用1、推广应用2.该题组让学生经历观察、猜想、证明、推广应用的过程，激发了学生的求知欲，培养了学生的应用意识.同时，使学生求真、理性，乃至创新的意识和能力都得以自然地生长.

基于教材例、习题，我们可以以思辨性题组的方式综合若干个方面（如图26）设计高质量的题组，或一题多变，或多题归一，以题组启发深度思考，以题组引领深度学习，教学要重视在思辨中求变通，在变通中求创新，培养学生主动探索的精神，从而能在创新中实现学生思维发展的目标，助力学生实现自我突破和素养发展.

图26