运用模式识别 探寻数学之美

刘志昂

（江苏省苏州高新区第五初级中学校）

在初中几何解题教学中，模式识别是一种很有效的策略，即在数学问题的解决过程中，所积累的知识和经验经过加工，会得出有长久保存价值或基本重要性的经典结构与重要类型——模式.当遇到一个新问题时，我们联想起已经解决的问题，便可以在记忆中提取相应的方法对新问题加以解决.在教学中，要注意引导学生抓住基本图形的基本结构，通过对基本问题的解决，得到基本结论，然后对原命题进行逆向变式，深度研究得到基本结论的思路和方法，构建出一个解决与基本图形相关问题的基本模式.在解决相关问题时，引导学生对之前构建的模式进行识别，运用模式中解决问题的策略、方法来解决新的问题.

这种解题策略，不仅可以缩短学生的思维路径，使问题得以尽快解决，还可以使学生获得成就感，产生满足感.法国著名数学家庞加莱认为，数学的优美感，不过是问题的解答适应我们心灵需要而产生的满足感.

一、模式识别

1.模式的构建

例1在正方形ABCD中.

（1）如图1，点E，F分别在BC，CD上，且AE⊥BF，垂足为点M，AE与BF是否相等？证明你的结论.

（2）如图2，如果点E，F，G分别在BC，CD，DA上，且GE⊥BF，垂足为点M，GE与BF是否相等？证明你的结论.

（3）如图3，如果点E，F，G，H分别在BC，CD，DA，AB上，且GE⊥HF，垂足为点M，GE与HF是否相等？证明你的结论.

图1

图2

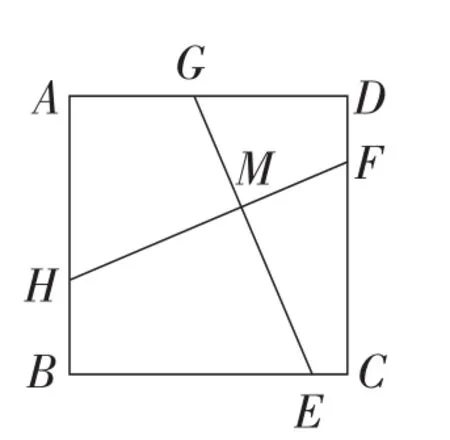
图3

此题主要考查正方形的性质，以及全等三角形的判定与性质.第（1）小题根据正方形的性质，得到∠ABE=∠BCF=90°，AB=BC.根据“同角的余角相等”可以得到∠BAE=∠CBF.则△ABE≌△BCF.进一步根据全等三角形的对应边相等得到AE=BF.第（2）小题中，过点A作AN∥GE交BC于点N（如图4），可证四边形ANEG是平行四边形.根据平行四边形的对边相等可得AN=GE.由第（1）小题的结论，可知AN=BF.所以GE=BF.第（3）小题中，分别过点A，B作AP∥GE，BQ∥HF（如图5），可证四边形APEG、四边形BQFH为平行四边形.根据平行四边形的对边相等可得AP=GE，BQ=HF.由第（1）小题的结论可知AP=BQ.所以GE=HF.

图4

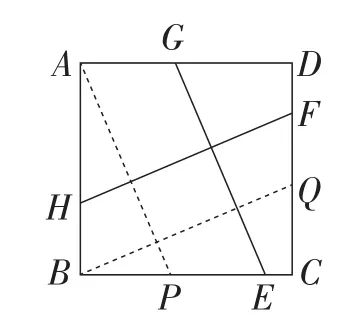
图5

在上面解决问题的过程中，第（1）小题是基础.由已知条件，借助正方形的直角和边，构造出全等的Rt△ABE和Rt△BCF，再运用全等三角形的性质来判断线段相等.而第（2）小题和第（3）小题则是通过平行移动将其转化为第（1）小题，依然是通过证明全等三角形，应用其对应边相等来解决问题.

在上述问题解决的过程中，我们构建出一个模式，即基本图形的基本结论、基本思路和基本方法.基本图形——正方形中，端点分别在两组对边上且互相垂直的两条线段；基本结论——这两条线段相等；证明这一结论的基本思路和基本方法——借助正方形的边和直角构造出全等的直角三角形，再运用全等三角形的对应边相等来证明上述线段相等.

构建这一模式后，在解决一些有关正方形中线段相等的具体问题时，遇到与之相同或相近的结构，便可以识别为这一模式，运用模式中的基本图形、基本结论、基本思路和基本方法来解决问题.解决具体几何问题时，要注意与已有知识和经验发生联系，将问题进行归类，使其与自己认知结构中的某种数学模式进行匹配，从而利用熟悉问题的解题思路找到新问题的解决方法.

2.模式的使用

（1）直接使用.

例2如图6，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为点D′，点C落在点C′处.若AB=6，AD′=2，求折痕MN的长.

图6

这个问题的解决，就是通过添加辅助线，识别出模式，将问题转化为模式中基本图形的基本结论，而具体解决问题的思路和方法与模式中的思路与方法一致.将问题转化为已经解决的问题，体现了模式识别中蕴涵的化归思想，体现出基本图形的基本结论、基本思路和基本方法的内在联系，缩短了学生的思维路径，使解题步骤得到简化.这是化生为熟的“熟悉化”原则，也是将问题分解为基本问题的“简单化原则”.

波利亚在《怎样解题》中指出，题目一旦获解，就会立刻产生情感上的满足，这恰好错过了提高的机会，事实上没有一道题可以解决得十全十美，总还有一些工作要做，经过充分的探讨与总结，总会有点滴的发现，而且在任何情况下，我们总能提高自己对这个问题的解答水平.显然，在这一问题的解决过程中，学生在孤立的数学图形中，找到了关联的图形，借此找到了问题的结论和解决问题的方法、思路，有利于建立图形整体结构，也体会了这些图形之间的内在联系，从而丰富了模式，更推进了模式的构建.

（2）转化使用.

例3（1）如图7，在正方形ABCD中，E，F分别是边BC，AB上的点，且CF⊥DE.过点E作EG⊥DE，使EG=DE，连接FG，FC.试判断：FG与CE的数量关系是_______，位置关系是_______.

（2）如图8，若E，F分别是CB，BA延长线上的点，其他条件不变，（1）中的结论是否仍然成立？试做出判断并给予证明.

（3）如图9，若E，F分别是BC，AB延长线上的点，其他条件不变，（1）中的结论是否仍然成立？试直接写出你的判断.

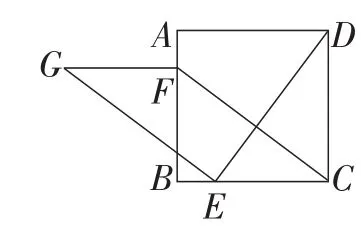
图7

图8

图9

第（1）小题中的CF⊥DE，且线段CF和DE的端点分别位于正方形ABCD的两组对边上，恰好是例1中构建的模式，故可以得到结论CF=DE，而证明的方法与模式中相同，都是先根据同角的余角相等，得到∠BCF=∠CDE，证明△BCF≌△CDE.结合已知条件EG=DE可以得到CF=EG，再根据CF⊥DE，EG⊥DE可以证明CF∥EG，得到▱CFGE.则FG=CE，且FG∥CE.

第（2）小题和第（3）小题中的CF⊥DE，且线段CF和BE的端点分别位于正方形ABCD的两组对边所在的直线上，依然运用模式中的方法，证明△BCF≌△CDE，得到CF=DE，再结合已知条件证明出▱CFGE，得到FG=CE，且FG∥CE.

以上三道小题，运用模式中的方法证明三角形全等，得到模式中的结论，缩短了思维路径.

在解决以上问题的时候，都是识别出模式，运用模式中的通法（三角形全等的证明），得到模式中的结论（CF=EG），然后结合已知条件，将其转化为平行四边形，进而解决问题.实则是一法多用，即对前面解法的归纳、总结，形成模式，并用以解决其他问题，从而达到问题解决的目的.

在解题教学中，运用模式识别这一策略解决问题时，要注意引导学生分析问题的特征，从整体上认识、把握问题的结构，对已有的模式进行识别.从思维的角度看，这里体现了思维正迁移的积极作用，遇新思陈、推陈出新就是为了在当前问题与头脑中已有的知识、经验、解决问题的方法之间建立联系，以诱发有积极意义的思维定势，完成知识、方法的正迁移，促进学生对图形间、知识间内在联系的认识，使其体会简洁的表现形式、精细的思考方法.

（3）变式识别使用.

例4如图10，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8 cm，动点P从点B出发，在BA边上以每秒5 cm的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以每秒4 cm的速度向点B匀速运动，运动时间为t秒(0 ＜t＜2 )，连接PQ，AQ，CP，若AQ⊥CP，求t的值.

图10

图11

我们不妨与例1的第（1）小题做比较，由正方形变为矩形，而全等也变成了相似，线段之间的相等关系随之变为成比例线段，代入数据后，得到方程，依然可以解决问题.这是模式的变式，我们用到的不再是模式中的结论，而是其中的解题思路和方法，这是将多个问题的共性抽取出来，是从模式中探究出来的解决此类问题的通法，并运用通法来解决类似的问题，其本身也是一种解题迁移（即先前的解题学习对后续的解题学习的积极影响），是一种有形与无形的关系.所以，我们在解题教学中，要突出对数学思想方法的归纳和总结，要充分展示模式的作用，并且在解题学习中注意概括解题模式.但是我们不能受模式的约束，而应该借助模式，找到其中蕴涵的思想方法，这才是模式中的一般方法，也是模式中蕴含的智慧.从而增强学生对数学基本思想的理解，增强学生对基本活动经验的积累，提高学生的数学解题能力.

二、美在其中

1.欣赏整体结构的美观

数学之美，还在于整体的结构.从例1到例4，在题目的结构上有一个共性——通过端点分别在正方形（或矩形）两组对边上的两条互相垂直的线段，构造出两个全等（或相似）的直角三角形，而解决问题的方法都是通过对全等三角形的证明得到相等的边，或是通过证明相似三角形得到比例线段，进而构造出方程求解.而从正方形到矩形、从全等到相似，则是一个从特殊到一般的过程，既有外部的美观，又有内容与方法上的统一，不仅注意外形上的分析，而且注意到内容上的理解，能从一个孤立静止的数学形式中找出关联活动的数学内容，体现了整体结构的美观.

从模式的构建到模式的运用，基于习题自身的特征以及解题方法的内在联系，构造出了一个CPFS结构，不仅能够让学生深刻理解数学知识，而且能够引导学生灵活运用数学知识，既训练了学生思维的深度和广度，又提高了其发现问题、提出问题、分析问题和解决问题的能力.

张奠宙先生认为，数学欣赏正在从外部的美观，不断的上升到数学概念和命题的内涵深处.欣赏外表直观之秀，内涵深刻之慧，文化底蕴之浓，理性思考之精，也许这就是数学欣赏的普遍规律.

2.领略内涵智慧的美妙

在模式识别中，例1中对所学内容整理归纳出类型和方法，把类型、方法和范例作为一个整体来积累，重视基本图形的基本结论、基本思路和基本方法，体现出对模式的积累.数学大师陈省身教授说过：一个好的数学家与一个蹩脚的数学家，差别在于前者有很多具体的例子，后者则只有抽象的理论.

由于数学是一门演绎推理的学科，所以任何一个已经被证实的结论都可以作为推断其他结论的依据.所以例2和例3则是化归为基本模式，在相同或者相近的结构中揭示题目的内涵.其实模式识别的过程就是对感觉信息与长时记忆中的有关信息进行比较，再决定它与哪个信息有着最佳匹配的过程，对模式的自觉使用过程，同时也是一种智慧.

例4的解决，则是对模式的转化和分解，是对模式的重组和创新，是化有形为无形，充分说明模式不应该是束缚思想的框架，而应该是思维腾飞的跑道.因而是一种模式的突破，这也充分体现了模式识别的内涵中蕴含的智慧.

教育学家夸美纽斯曾经说过：提供一种既令人愉快又有用的东西，当学生的思想经过这样的准备之后，他们就会以极大的注意力去学习.由于以上各例题之间有着内在的联系，而解题方法又是这样的相似.因此会激发学生的兴趣，激发他们学习的兴奋点，激励他们努力的探究下去.

3.感悟理性思考的美感

从例1到例4的模式的构建与识别运用，从思考方式看，用模式中简洁的方法去解决问题，可以将复杂的问题化归为模式来解决.这种由浅入深的过程，体现了自然之美和艺术之美，在欣赏数学之美时，不应该停留在感官的刺激上，而要用理性的思考去品味.因此在解决问题之后，教师也应该引导学生去反思.首先对自我解决问题的行为进行反思：我的答案是否正确？我的方法是否唯一？解决这个问题的关键在哪里？解决这一类问题的思路是什么？其次对问题本身进行反思：这个问题的逆命题成立吗？（如例3）将条件适当变化后会有什么不同的结论？这一结论与原结论之间有什么关系？这个问题如何推广？等等.这种基于问题的反思中蕴含着一种批判性的思维方式，同时也是一种发散性思维，这本身也是一种实践智慧.

张文俊教授在《数学欣赏》一书中指出：数学的美就是数学问题的结论或解决过程中为了适应人类的心理需要而产生的一种满足感，简洁的表现形式，精细的思考方法，处处充满着理性、高雅、和谐之美，这是真与善的客观表现.

4.满足心灵需要的美满

从上述例题的解题过程中，学生会获得一种成功的体验，满足了学生自我实现的需要，同时获取了一种积极的情绪.积极心理学认为：积极情绪扩大了一个人在特定情境下瞬间的思想和行为指令系统，能在当时特定的情境下促使人们冲破一定的限制而产生更多的思想，出现更多的行为或者行为倾向.显然，基于这种积极的情绪，可以使学习数学和愉快情绪之间建立稳定的联系，激发学生对数学学习的兴趣，促进学生学好的愿望和信心.

法国数学家笛卡儿认为：一般地说，所谓美和愉快，所指的不过是我们的判断和对象之间的一种关系.凡是能使大多数人感到愉快的东西就可以说是最美的.学生探究成功之后的喜悦，会是一种愉悦的心情与体验，会激发学生学习数学的兴趣，增强学生学习数学的信心，这当然也是一种满足心灵需要后的美满.