对一道江苏模拟椭圆题的破解
2019-06-22 06:18江苏省仪征市第二中学周国梅
中学数学杂志 2019年11期
☉江苏省仪征市第二中学 周国梅
☉江苏省仪征市第二中学 沈永明
纵观近几年高考数学试卷中的解答题,发现涉及圆锥曲线中的椭圆类的题目出现的频率非常高,亮点也颇多.处理好此类问题,除了要熟练掌握椭圆的定义、方程与几何性质,还要充分结合题目中的已知条件,与其他相关的知识加以交汇与综合,可以从椭圆自身的角度出发来破解,也可以从相关知识的角度出发来破解,殊途同归,真正达到快速、有效、准确解题的目的.
一、问题呈现
问题(2019届江苏省某市高三年级第一学期期末教学质量调研·18)如图1所示,已知椭圆的离心率为右准线方程为x=4,A,B分别是椭圆C的左、右顶点,过右焦点F且斜率为k(k>0)的直线l与椭圆C相交于M,N两点.
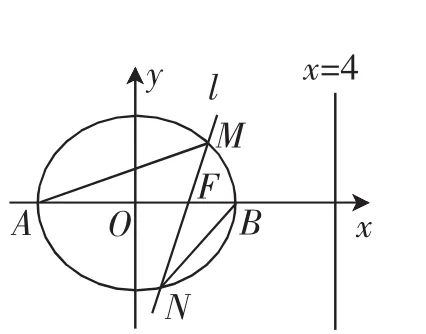
图1
(1)求椭圆C的标准方程;
(3)设线段MN的中点为D,直线OD与右准线相交于点E,记直线AM,BN,FE的斜率分别为的值.
二、问题破解
解析:(1)设椭圆的焦距为2c(c>0).




三、规律总结
探索圆锥曲线中的定值问题,往往可以发现点、直线、圆、圆锥曲线等知识之间的内在联系与规律,从而加强对相关内容的正确理解与掌握,有助于数学解题能力与应用能力的提高,真正提升数学能力,拓展数学素养.
猜你喜欢
江苏安全生产(2022年4期)2023-01-16
江苏安全生产(2022年5期)2023-01-15
中学数学研究(江西)(2022年5期)2022-05-08
华人时刊(2021年23期)2021-03-08
河北理科教学研究(2020年2期)2020-09-11
物理之友(2020年12期)2020-07-16
——五年级“异分母分数加法和减法”教学例谈
数学大世界(2020年14期)2020-07-06
中学数学研究(江西)(2019年6期)2019-07-08
福建中学数学(2016年7期)2016-12-03
福建中学数学(2013年1期)2013-03-06

