基于数学核心素养的不同版本教材比较研究
——以“函数的单调性”为例
☉广东省深圳市横岗高级中学 闻 雷
《普通高中数学课程标准(2017年版)》(下简称《课标》)指出:“基于数学学科核心素养的教学活动应该把握数学的本质,创设合适的教学情境、提出合适的数学问题,引发学生思考与交流,形成和发展数学学科核心素养.数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.”
本文基于数学核心素养,以“函数的单调性”为例,从情境与问题、定义、例题、习题四个维度比较人教A版、人教B版、北师大版和苏教版的教材内容.
一、情境与问题
教学情境包括现实情境、数学情境、科学情境,数学问题是指在情境中提出的问题.数学学科核心素养在学生与情境、问题的有效互动中得到提升,因此教学中应注重数学情境的创设与数学问题的提出.下面是四个版本中的数学情境:
人教A版:观察f(x)=x、f(x)=x2的图像,从左到右观察图像上升(下降).以f(x)=x2为例,列出x与y的对应值.对比图和表,发现随着x的增大,f(x)的变化情况.
人教B版:考察图像,看出当自变量在实数集内由小变大时,函数y=2x、y=-2x、y=x2+1的值在逐渐减小(增大).
北师大版:y=x+1、y=x2在定义域内,函数值随自变量的增大而增大(减少),从图像上看从左到右是上升(下降).
苏教版:气温θ是关于时间t的函数,记为θ=f(t).观察气温θ关于时间t的变化图(图1),说出气温在哪段时间内是逐渐升高的或下降的.

图1
苏教版的情境是现实情境,是生活中的实例,能引起学生学习数学的兴趣,激起学生的好奇心.另三个版本的是数学情境,给出了要研究的问题,指明了解决问题的方向,但过于直接、平淡.四个版本中数学问题的提出如表1,人教A版设置的探究问题,随着问题的深入学生会产生认知冲突,诱发思考,唤起问题意识,通过思考解决问题.综合来说,笔者认为苏教版的情境与人教A版的问题设置比较好.
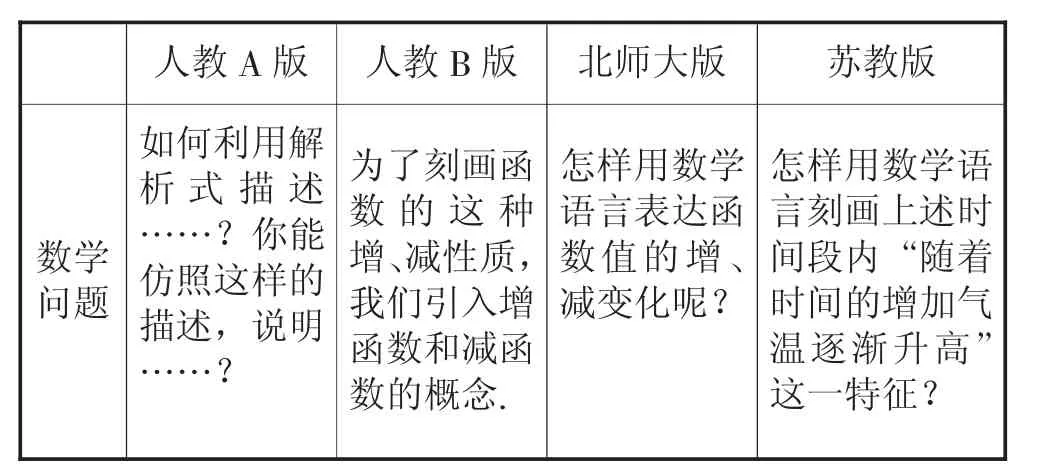
表1 四个版本中数学问题的提出
二、定义
数学概念、数学定义是数学的灵魂,是解决问题的逻辑基础.函数的单调性是函数性质的基础,教师应重视对其的教学,在定义生成的教学过程中落实核心素养.四个版本的定义过程如下:
(0,+∞)上是增函数.引导探究减函数,进而给出一般化的定义.
人教B版:在函数y=f(x)的图像上任取两点A(x1,y1),B(x2,y2),记Δx=x2-x1,Δy=y2-y1.在函数定义域的某个区间M上任取两个值x1,x2,若Δx>0,则当Δy>0时,就称函数y=f(x)在区间M上是增函数.又给出减函数,进而给出一般化的定义.
北师大版:在函数y=f(x)的定义域内的一个区间A上,如果对于任意两数x1,x2∈A,当x1<x2时,都有f(x1)<f(x2),那么,就称函数y=f(x)在区间A上是增加的,有时也称函数y=f(x)在区间A上是递增的.又给出递减的情况,进而给出一般化的定义.
苏教版:直接给出一般化的定义.
数学抽象是指通过对数量关系和空间形式的抽象,得到数学研究对象的素养.对比表2,三个版本教材(除苏教版外)的定义过程,基本上都是从图形语言“上升、下降”到自然语言“增大、减少”,再到数学符号语言“增函数、减函数”.在这种数学活动的体验中,经历从具体的直观描述到形式化的符号表达的抽象过程.苏教版教材通过情境,直接给出定义的方式没能体现出数学抽象的学习过程.

表2 四个版本定义生成的特点及共同点
从特殊到一般(归纳、类比等)的推理是逻辑推理的两种类型之一.比较而言,人教A版的类比探究“你能仿照这样的描述,说明……是减函数吗?”设置的比较好.有逻辑地表达与交流是逻辑推理的主要表现之一.遗憾的是四个版本的教材对于关键点“任意”、“都有”没作出引导分析,而是直接用在定义中.在教学中,教师可以设置问题层层引导学生思考,在思考中体会从有限到无限的符号化过程,体会“任意”两字的逻辑严谨性.
三、例题
例题的“例”字说明了它的示范、代表作用.教材通过例题引导学生进一步理解知识,并用知识解决问题.四个版本的例题都是判断和证明函数的单调性,具体如表三.定义法证明常见函数的单调性,可帮助学生进一步理解函数的单调性,培养学生数学证明的严谨性,提升学生的运算能力,帮助学生打好基础以便灵活处理与函数单调性有关的其他问题.
四个版本的教材例题都涉及反比例函数,其图形直观地说明了函数单调性为区间上的性质.对比表3,发现人教A版探究研究处理较好.学生通过图像观察和定义证明,真正明白f的单调减区间为(-∞,0)和(0,+∞),而非(-∞,0)∪(0,+∞).

表3 四个版本例题
四、习题
习题的“习”字说明了它的实践、练习作用.及时练习,能进一步用所学知识解决问题,实现对知识的拓展和迁移,在练习中深化学习,在练习中提升素养.习题也可以反馈教学效果,从而进一步指导教学.
对比表四,四个版本的习题把题目至少分成两个层次,注重了学生的差异,体现了“以学生发展为本”的新课程理念.从表四看出苏教版的习题比其他版本的题目类型和涉及的知识点更多,便于学生的深入学习和探究提升,但其题量过大,为人教A版的2倍多.教师需根据学生的实际和教学的要求作适当删减和分类分层练习,实现不同学生在数学上得到不同的发展.
教学中精选课程内容,处理好数学核心素养与知识技能之间的关系.表4中的相同类型题目为四个版本共有的,应该在教学中着重关注.
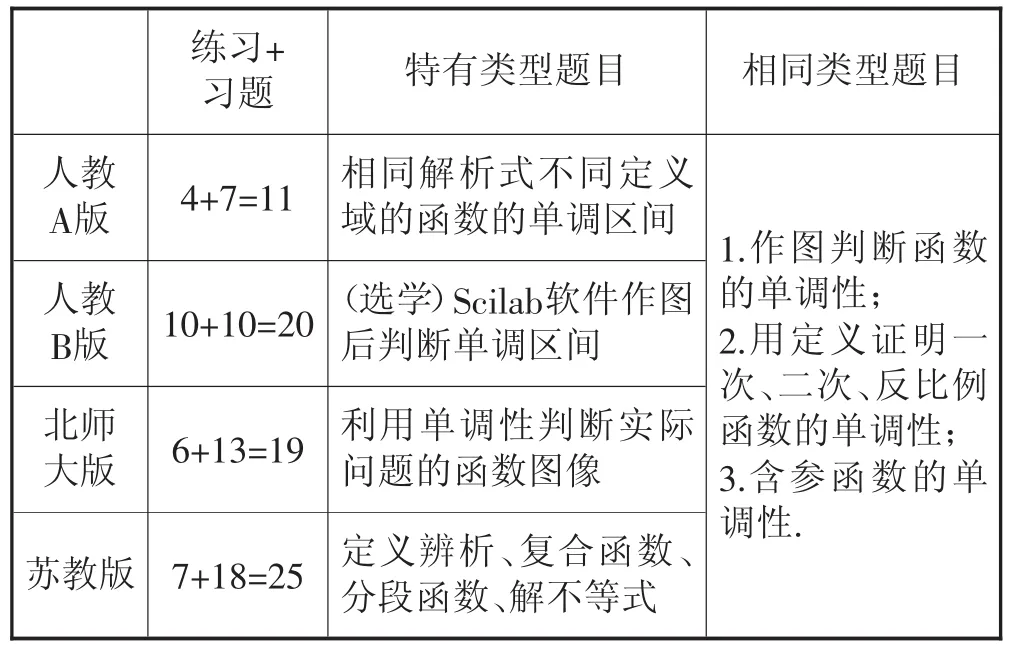
表4 四个版本习题(包括习题与练习,每道小题按1道题目来计算)
各版本习题明显比例题的难度大,尤其是在题意分析和数学运算方面.数学运算是解决数学问题的基本手段,能促进学生数学思维的发展,培养认真严谨的学习态度.数学运算是一种演绎推理,具有程序性.定义法证明函数单调性的思路很明确,在教学中教师应引导学生提炼出“设元、作差、变形、断号、定论”的基本运算程序.
五、结束语
《课标》指出:“发展学生数学核心素养是学科课程的核心目标,是教材编写的宗旨.编写教材应遵循学生的认知规律,创设合适的问题情境,设计有效的数学学习活动,展示数学概念、结论、应用形成发展过程.”各版教材凝聚着编者的心血与智慧,具有其独特的风格与特色.教师在教学中应结合学情,汲取各版教材精华,让核心素养在课堂上落地生根.

