对一道解析几何考题的探究与拓展

☉江苏省泰兴中学 钱继兵

解析几何是高中数学的重要内容之一，其知识点覆盖广、综合性强、典型问题多，对学生的数学运算和分析推理能力要求较高，本文将以一道解析几何问题为例，探究其解析方法，并对其模型和原理进行提炼拓展，与读者交流学习.

一、考题呈现

题目已知椭圆的解析式为3x2+y2=λ，点A，B是椭圆上的两个点，而点N（1，3）是线段AB的中点，作线段AB的垂直平分线与椭圆相交于C，D两点.

（1）试确定参数λ的取值范围，并求直线AB的方程；

（2）试判断是否存在一定值λ，使得A，B，C，D四点在同在一个圆上？并写出分析过程.

分析：本题目为直线、圆和椭圆相融合的解析几何题，考查学生的基础知识和分析推理能力，从知识领域来看，涉及代数和几何两大模块，是知识综合类考题的典型代表.在求解分析时需要基于几何知识来构建相应的模型，并结合几何性质和代数方程来透视几何结构，寻求解答问题的思路.

二、思路探究

（1）第一问求解椭圆特征参数λ的取值范围以及直线AB的方程，对于该问需要从题干中提炼出几何的特征条件，主要有两个：一是椭圆与AB所在的直线有A和B两个交点，二是点N是线段AB的中点.由条件一设出直线AB的方程，与椭圆方程联立构建方程组，则需要确保Δ＞0，而根据后一个条件则可以利用待定系数法化简相关参数，构建相应的不等式.

设AB所在的直线方程为y=k（x-1）+3，与椭圆方程联立可得：（k2+3）x2-2k（k-3）x+（k-3）2-λ=0 ①，设点A和点B的坐标分别为（x1，y1）和（x2，y2），则其中x1和x2就为方程①的两个不同的根，所以满足Δ＞0，即4［λ（k2+3）-3（k-3）2］＞0 ②，点N（1，3）为线段AB的中点，则x1+x2=2，同时联立两者可解得k=-1，所以直线AB的方程为y=-（x-1）+3，即x+y=4，而将k=-1代入②式，化简后可得λ＞12，所以λ的取值范围为（12，+∞）.

（2）第二问探究是否存在一个合适的值λ，使得A，B，C，D四点在同一个圆上，首先需要明确四点共圆需要满足的条件，然后根据条件构建相应的求解模型.假设A，B，C，D四点可以在同一个圆上，则可能存在值λ，使得以A，C，D为顶点的三角形为特殊三角形，则其中必然存在对应的几何线段关系，因此只需要分析其合理性即可.

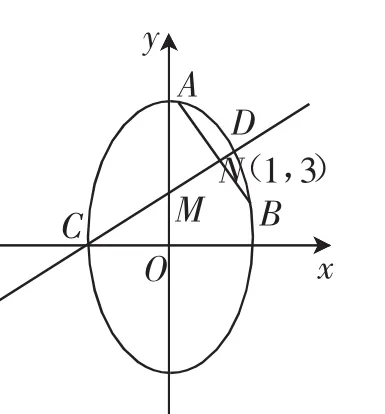
图1

已知AB的垂直平分线为CD，则根据AB所在直线的方程可以得到CD所在直线的方程，即lCD：x-y=-2，将其与椭圆方程联立，整理得4x2+4x+4-λ=0 ③，设点C和点D的坐标分别为（x3，y3）和（x4，y4），线段CD的中点为M（x0，y0），则其中x3，x4是③式的两个根，即x3+x4=-1，而，点M的坐标满足方程x-y=-2，可解得点M的坐标为于是利用弦长公式可求得|CD|=.同理联立AB所在的直线方程与椭圆方程，可得 弦 长经 分 析 可 知 当 λ ＞12时 ，，即|AB|＜|CD|.假设λ＞12时，A，B，C，D四点共圆，则CD必为圆的直径，点M为圆心.过点M作线段AB的垂线且垂足为点E，连接AM、BM，如图2，由点到直线的距离公式可得|ME|根据几何性质可知△MEA为直角三角形，由勾股定理可得|ME|2+|AE|2=|AM|2，即此值恰好与故可知当λ＞12时，A、B、C、D四点共圆.

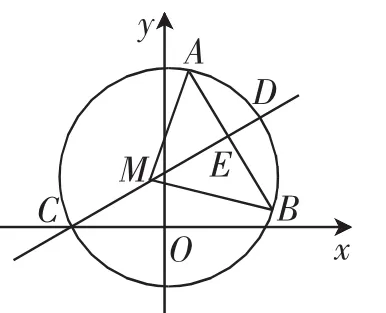
图2

三、另解拓展

对于上述几何与代数知识相结合的解析几何问题，其解法思路是多样的，除了可以沿用上述传统的解法来探究外，也可以变换角度，从其他角度进行剖析，开展考题的多解探析对于考题的结构认识和解题策略的积累是十分有利的，下面对其进行深入探析.

1.关于第一问

上述第（1）问是基于问题构建的条件开展的思路探索，而求解AB所在的直线方程实际上就是求直线的斜率k，可以从直线斜率的定义出发来构建求解模型.对于参数λ的取值范围，则可以考虑从点在椭圆中的位置关系的角度来分析.

设点A和点B的坐标分别为（x1，y1）和（x2，y2），则线段AB的斜率可表示为，点A和点B均位于椭圆上，则必然满足椭圆方程联立两者可变形为3又因为点N（1，3）是AB的中点，所以x1+x2=2，y1+y2=6，代入上式可解得kAB=-1，所以AB所在的直线方程为x+y=4.已知点N（1，3）在椭圆的内部，则λ＞3×12+32=12，所以λ的取值范围为（12，+∞）.

2.关于第二问

上述考题在求解第（2）问时，基于假设在圆内构建了特殊的三角形，根据勾股定理建立了关于线段长的代数模型，然后确立了四点共圆的合理性.对于该问还可以从向量角度入手，若A、B、C、D四点共圆，考虑到线段CD是AB的垂直平分线，则圆心必然位于线段CD上，从而以点A、C、D为顶点构建的△ACD必然是直角三角形，且角A为直角，于是从向量角度出发有C■→A·D■→A=0，因此只需要结合已知条件对其加以验证即可.

线段CD所在的直线方程为x-y=-2，线段AB所在的直线方程为x+y=4，分别与椭圆方程联立可得4x2+4x+4-λ=0，4x2-8x+16-λ=0，由两式可得经计算可得所以可确定点A位于以CD为直径的圆上，而点B是点A关于线段CD的对称点，故也位于圆上.因此存在一定值λ，使得A，B，C，D四点在同一个圆上.

四、反思建议

四点共圆作为解析几何中较为特殊的问题，其探究思路以及分析方法具有一定的代表性，即对于其中的几何问题，除了需要充分利用题干中相关曲线的方程外，还需要利用几何性质构建相应的解析模型，最终通过证明模型中的特殊关系来确定四点共圆的合理性.因此该类问题求解的背后是数形结合思想方法的渗透与应用，在教学中需要指导学生掌握运用数形结合来解题的方法步骤，深刻理解该方法的思想内涵，形成用数形结合解析问题的意识.

开展考题探究学习除了要掌握相应的解题方法外，从考题中提炼相应的解析模型也是其意义所在.如上述考题在探究四点共圆之后，对问题模型和方法原理都进行了提炼，并从中总结出一般四点共圆类问题的定理和推论，并将其拓展应用到变式问题中，实现了同类型问题的高效求解.因此在平时的教学中，教师不应局限于考题的方法讲解，要注重对考题原理的提炼与拓展，指导学生提炼出解析模型，并对考题进行深度研究，力求实现“解一题，通一类”的教学目的，从本质上提升学生的解题能力.