基于HyperWorks的油底壳约束模态分析
胡 明,龚俊杰,胡 旭,杨丽华
(广西大学机械工程学院,广西 南宁53000)
0 前言
以4H发动机为载体,采用HyperWorks软件进行模态分析,验证发动机油底壳有限元模型约束模态的准确性。
1 实物三维模型的建立
该4H发动机油底壳模型是由三维逆向工程扫描而成,其都为面模型,所以在CATIA软件中对实物模型生成实体模型,如图1所示。
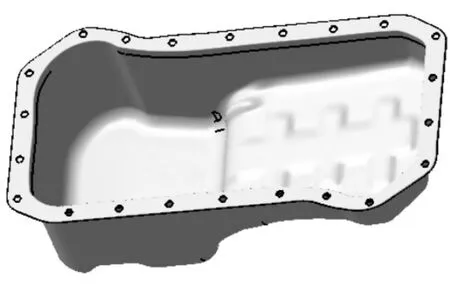
图1 4H发动机油底壳实物模型
如图2所示,油底壳空壳状态网格划分结果。对油底壳模型进行网格划分之后,产生的单元个数为16 737个,节点数为16 742个,单元质量检查comp.QI=0.01,单元不合格率为0%。网格划分质量好,其结果如图3所示。

图2 网格划分
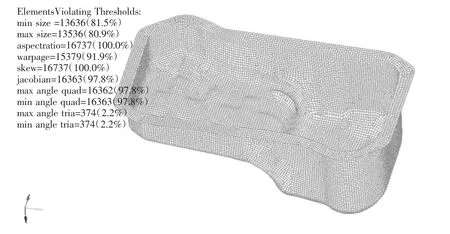
图3 单元质量检查
2 模态分析基本理论
模态分析是研究结构动力特性的一种近代方法,是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析得到,这样一个计算或试验分析过程称为模态分析。进行模态分析,要求解的固有频率和振型参数通过动力学方程求得[1-2]:
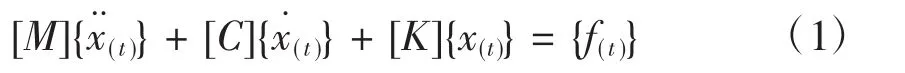
固有模态与外载荷无关,即{f(t)}={0},则得到系统的自由振动方程。在计算系统固有频率和振型时,结构阻尼的影响很小,忽略不计的情况下,动力学方程简化为:

这个是常系数齐次微分方程组,其解的形式为:
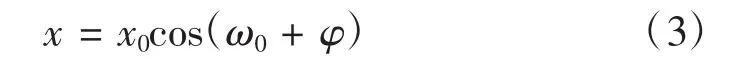
式中:ω0为振动固有频率,φ为振动初相位。
将式(3)带入式(2)便得到齐次线性代数方程组:
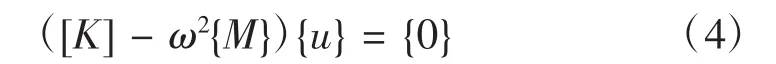
3 等效质量法油底壳的约束模态仿真分析
油底壳在发动机上是固定的,其存在约束,所以对油底壳进行约束模态分析。油底壳的实际工作约束是通过螺栓固定在发动机上,因此,对油底壳的螺栓孔施加六个自由度的固定约束,以空壳状态为例,如图4所示。

图4 油底壳的约束
等效质量法[3]:发动机油底壳装油状态下采用的是等效质量法求解模型的自由模态下的频率与振型,即油底壳的除了密度,其它材料特性属性不变,将油底壳壳体分为是否与机油接触的两个部分,计算机油的质量,将这部分质量附于与机油接触的壳单元。
该油底壳的力学参数为:弹性模量E=2.0×105MPa,泊松比μ=0.3,密度为7 900 kg/m3,厚度为1.575mm,机油密度0.91×103kg/m3.
定义油底壳的单元类型为四节点壳单元,将材料属性附与壳单元,再定义载荷工况与载荷步,最后采用Optistruct进行模态求解。
发动机油底壳装油状态下采用的是等效质量法求解模型的约束模态下的频率与振型,即油底壳底除了密度,其它材料特性属性不变,将油底壳壳体分为是否与机油接触的两个部分,计算机油的质量,将这部分质量附于与机油接触的壳单元。以装3.5 L机油状态为例,需要建立两种材料,上部分的材料属性仍不变,密度为7 900 kg/m3,下部分的其他材料属性一致,密度经计算后为27 205.5 kg/m3。其有限元单元网格模型如图5所示。同理,装7 L机油状态如图6所示。

图5 3.5 L机油状态

图6 7 L机油状态
油底壳空壳状态、含3.5 L机油状态和含7 L机油状态的前六阶约束模态结果分如表1、表2和表3所示。振型结果如图7、图8、图9所示。
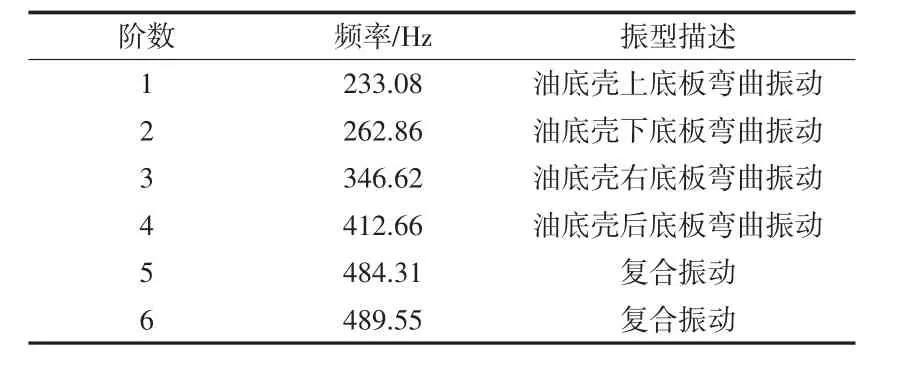
表1 油底壳空壳状态前6阶约束模态频率值
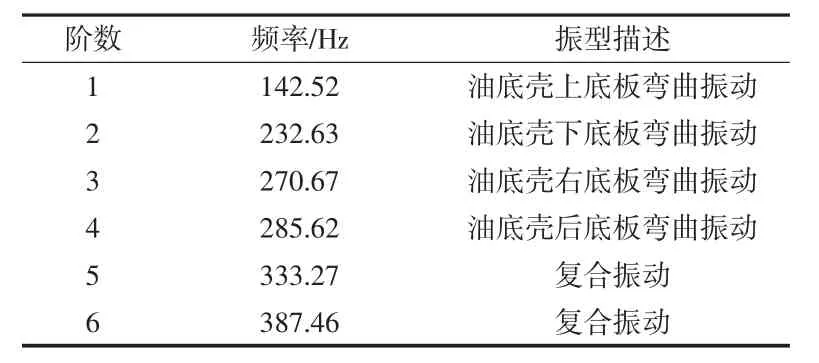
表2 油底壳含3.5 L机油状态前6阶约束模态频率值
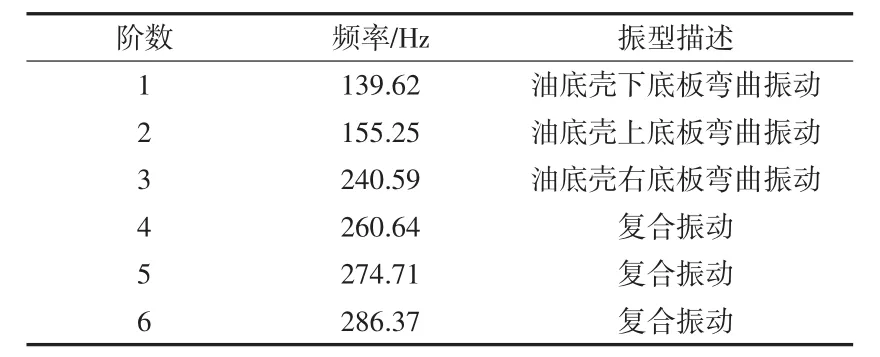
表3 油底壳含7 L机油状态前6阶约束模态频率值

图7 油底壳空壳状态前六阶约束模态振型

图8 油底壳含3.5 L机油前六阶约束模态振型
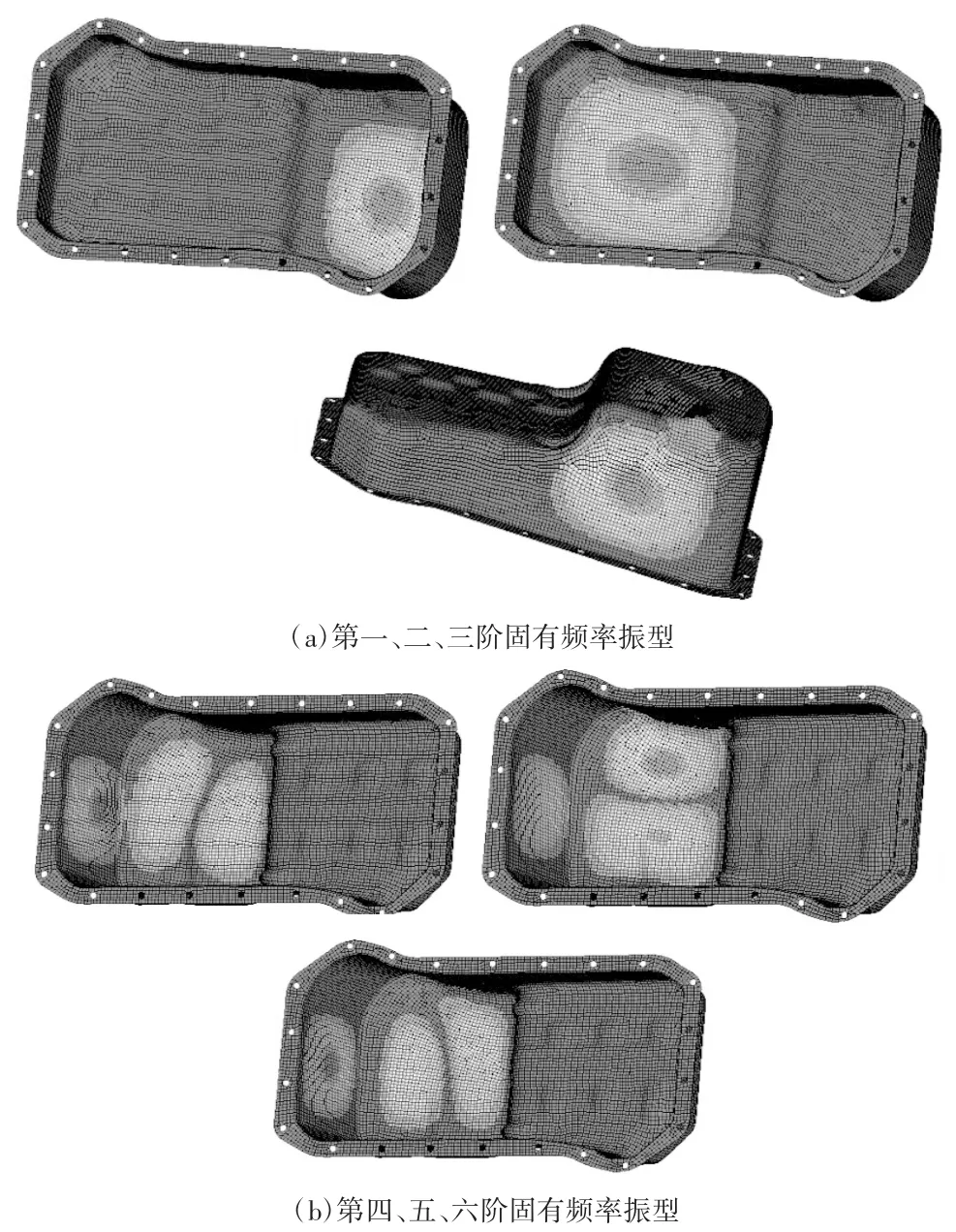
图9 油底壳含7 L机油状态前六阶约束模态振型
由结果可知,含油量影响油底壳的约束模态,而且影响比较大,随着含油量的增多,同样阶次的固有频率降低,同阶频率空壳状态固有频率下降的幅度较大。
至于该油底壳这三种状态下的固有频率的振型,第一阶频率下的振型,空壳与含油状态的振型基本是一致的,都是整体的一阶扭转。第二、三、四阶固有频率下的振型振动最大的位置都是出现在油底壳的上下底面,从第四阶开始,油底壳的振型为复合振动。
4 结论
(1)约束模态前六阶固有频率随着含油量的增加会降低。
(2)约束模态下,前四阶固有频率振型最大的位置都出现在上下底板,四阶以上固有频率的振动则为复合振动。

