自觉课堂中的三角板摆放
胡珏

【摘要】七年级部分学生在学习几何内容没多久就开始出现明显学习掉队现象,造成他们困惑的原因之一就是识图困难.教师在教学过程中充分利用三角板,让学生在自己动手摆放的过程中,识别三角形中的角与角的关系、寻找基本图形,由此培养学生从复杂图形中抽象出基本图形的意识以及学生的识图能力.
【关键词】自觉课堂;三角板;运动角度;基本图形
一、学习困惑
七年级学生在学习几何时常会感到困难,造成困难的原因主要有这样的两个方面.首先是学生自身的思维发展局限性.这个年龄阶段的学生处在具体形象思维向抽象逻辑过渡的时期,且具体形象思维占据主体较多.在面对几何学习时,他们可以熟背教师给出的定义、性质等,但将文字语言转化成图像信息,或者从图像中提取信息转化成文字语言对他们而言是有难度的.所以,我们常会见到在图形中找不到相等的角或相等的线段的同学.
这样,学生学习几何渡过了最初的简单识图、基础概念学习的新鲜期后,就会有一部分开始掉队,出现在较复杂的图形中无法寻找到基本图形的情况,长此以往,他们就成为班里所谓的学习几何的学困生.教师采取怎样的教法能尽可能地帮助学生解决困惑?如何在学习几何之初,就帮助学生培养识图能力?
二、解决方案
经过上述分析,不难看出识图是几何学习的必备能力,在初中阶段,大部分的几何图形依托三角形展开变化.如轴对称图形中的等腰三角形是由直角三角形沿某一条直角边翻折得到,再如,中心对称图形中的平行四边形是由三角形以某边中点为旋转中心,旋转360°得到.
另一方面,三角形是指三条线段收尾顺次相连围成的封闭图形,所以,三角形中涉及了线段和角的知识.两块三角板通过平移、旋转、翻折等运动变化,又可以构造出各种图形,三角形的全等、相似知识点的考查大多是在这些图形中探究.
所以,以三角板为学习工具,在通过对三角板各种不同摆放的图形过程中寻找基本图形,以增强学生识图能力.
同时,自觉课堂是学生活动的载体,在课堂中学生摆脱以往教师讲或者在教师的引导下看纸上所画图形,然后根据图形解决问题的模式,而是利用三角板这个载体让学生在多维互动中实现“自觉地”自主生成,给学生“创造”和“再创造”的机会.由此给了学生自己搭建抽象思维与具体形象思维之间的阶梯.
三、方案的具体操作
(一)三角板之初体验——摆放静态的图形
教师所有教学活动展开的依据主要是立足书本,新课程提倡“材料式”的教材观,即教材是教师教和学生学的材料,是教学资源之一,其根本特征是“范例性”.
如苏科版七上第154页“想一想”中要求学生“如何画一个角等于已知角”,特别强调
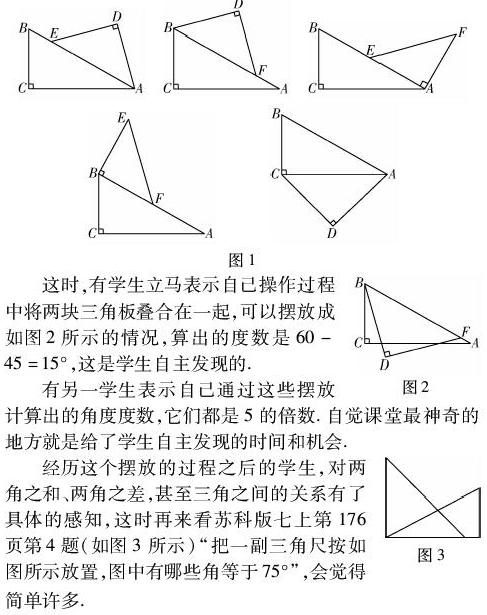
一些特殊角可以用一副三角尺画出.三角板自身的特殊角度有30°,45°,60°,90°.除这些角度外,还可以画出哪些角度呢?两块三角板不叠合在一起,可以摆放成如图1所示.
这时,有学生立马表示自己操作过程中将两块三角板叠合在一起,可以摆放成如图2所示的情况,算出的度数是60-45=15°,这是学生自主发现的.
有另一学生表示自己通过这些摆放计算出的角度度数,它们都是5的倍数.自觉课堂最神奇的地方就是给了学生自主发现的时间和机会.
经历这个摆放的过程之后的学生,对两角之和、两角之差,甚至三角之间的关系有了具体的感知,这时再来看苏科版七上第176页第4题(如图3所示)“把一副三角尺按如图所示放置,图中有哪些角等于75°”,会觉得简单许多.
纸上画的几何图形,对学生而言,就是图形,是抽象的.但是,三角板是学生可以拿在手中的,是具体形象的.它的出现是帮助学生实现了具体形象的物体到抽象图形的过渡.另外,摆放三角板的过程本身就是一个要求学生参与的动手实践过程.学生在操纵的过程中的感知体验明显强于单纯地对着图形看.
(二)三角板之再体验——呈现动态过程
在学习苏教版八上的“1.2全等三角形”這一内容时,图形的复杂程度明显增加,部分学生感到从图形中找出对应的线段或角都是较难的一件事.造成这样错误的原因主要还是学生自身对两个三角形这样的基础图形认识不足.在他们的意识里,线段就是一条条独立存在的,角也是如此,并没有从整体角度去看图,所以,才会出现找不清楚全等三角形的对应线段和对应角的情况.
准备两块含30°角的三角板,运用平移、旋转、翻折的运动方式摆放出新的图形(两块三角板可以有重叠).这样,可以摆放出如图4所示的典型图形,也可以更多别的图形.
在学生摆放时,要求把摆放出的图形画下,并找出图中相等的线段和相等角.这样,三角板再次帮助学生实现了从具体实物到抽象图形的过渡.特别是因为经历了自己动手摆的过程,对全等三角形的对应线段、对应角感受深刻,有效突破了在学习这一知识时的识图难点.
在从运动的角度摆放两块全等的直角三角板后,教师再将其一般化为两个全等的锐角三角形或钝角三角形时(如图5所示),学生自然会联想到之前摆放直角三角板时所找的相等线段、相等角.这时,再要求学生分别说出图5中的一个三角形经过怎样的运动就与另一个三角形重合.
从运动的角度看图形让学生在识图时有了整体意识,不再是孤立地看线段和角,而是站在了线段或角是属于哪个图形这样更高的位置,为解决判断两个三角形是否全等的问题作了充足的知识储备.另外,也为以后要学习的判断两个三角形是否相似做了铺垫.
经历了这些动态三角板摆放出的各种图形后,相信很多善于观察的学生发现图形可以是千万种,但是,这些诸多的不同中总有些相同之处.这些相同之处,就是他们自己抽象出的基本图形.这种抽象如果单纯地依靠学生自己的空间想象力实现是有一定难度,但是有了三角板这个实物摆放,明显是帮助他们降低了思维难度.
几何图形之间的联系既表现在它们的共同性,也表现在它们的差异性上.所以,教师在教学时要注意舍得花时间给学生,让他们观察复杂图形,从找出与他们题目间的共性与差异性.培养他们从复杂图形中抽象出本质的意识和能力.同时,使同学们在对比与查找的过程中,享受到数学学习的快乐,培养起学生学习数学的兴趣.
综上所述,三角板是帮助学生破解识图难的极好的工具.它是学生从具体形象思维向抽象逻辑思维过渡的桥梁.苏科版教材中也一再用到了三角板作为几何学习的切入口.在教学时,教师可以充分发挥三角板的妙用,给足学生摆放的时间,让他们在具体感知中熟悉线段、角,摸索归纳出基本图形,为以后的学习打下坚实的基础.
【参考文献】
[1]王锋.玩转三角板 猜想自然来[J].初中生辅导,2018(Z1):95-98.
[2]汪健.巧用三角板,优化初中数学课堂[J].考试与评价,2014(3):57.
[3]何笑琴.优化课堂教学 提高学生素质[J].黑河教育,2001(2):22-23.

