高中数学作业模式的改革与尝试

张强

[摘  要] 作业作为学生巩固提高，教师检测评估的重要手段，一直以来都是教学中的重要一环，为了更好地发挥作业的重要作用，教师应对作业设计与布置进行不断的尝试、改革和研究并因此为教师的“教”和学生的“学”提供更好的服务. 文章对传统作业布置模式进行了分析，对其不足之处进行了一定的剖析，同时通过对本校学生的调查，找出了存在已久的问题，并分享了我校已经采取的作业形式改革.

[关键词] 作业;自选作业;分层设置作业;自编作业

作业这一教学工作必要的环节一直为教师和学生所关注和重视，“减负”、“增效”等口号的提出也令人们对作业更为关注. 事实上，作业不仅能让学生巩固课堂学习的知识，加深对知识点的掌握程度，还能暴露出学习中的误区和盲点，让教师得以评估和检测学生的学习情况，从而能够相应地调整教学策略. 因此，教师应妥善安排好作业并对作业进行分析和反思，使学生能够在有意义的巩固练习与反馈中获得自学能力与实践能力的提升，这对于教学方法的改进也同样具有积极的意义.

[?]传统的高中数学作业

在传统教学模式下，教师一般会参照高考的要求和内容来安排作业，一般来说，作业就是教师根据习题难度所综合而成的训练链，包含基础题、提高题与竞赛题，教师期待学生在重复、机械的训练中得到知识的巩固与记忆，在有梯度的练习下逐渐加深对知识点的掌握和应用程度. 为了考察传统模式下的作业布置，笔者在其他老师的协助下对部分年级的作业布置情况进行了统计和调查，下表即为我校高一年级数学备课组在2016年10月到12月的作业布置及统计情况.

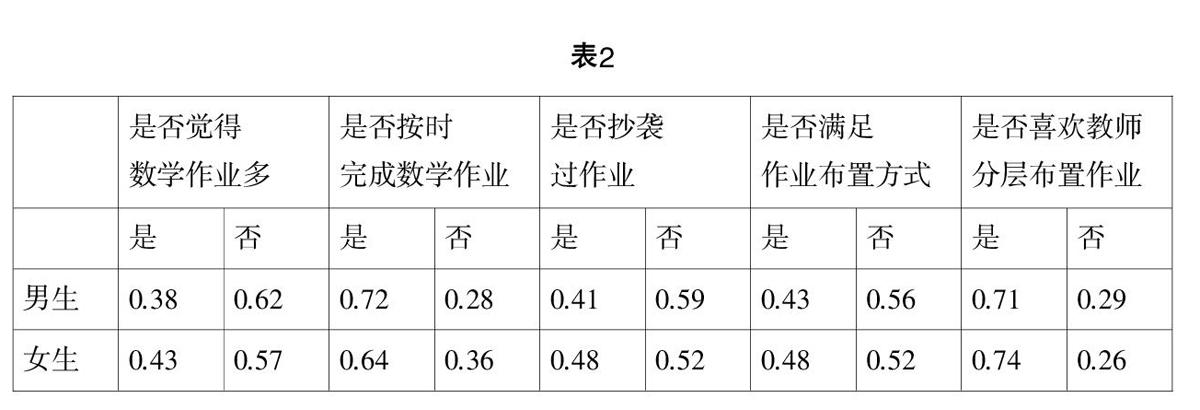
作业形式单一、量大且未经整合的作业布置情况在表1中很容易看出，由此可见，当时的作业布置太过注重作业的形式，而忽视了作业的本质作用和完成过程，学生宝贵的学习时间因为这样的作业布置而大大地浪费了. 不仅如此，学生在这样的作业中根本很难体会作业的意图，很多时候，他们会将作业看作是一种重复机械的任务，看作是一种负担，在这样的心态下，学生会渐渐不求甚解，只图能够完成作业，作业完成自然会大有难度，学生完成作业的积极性也会因此大打折扣[1]. 为此，我校高一年级数学备课组也对所有高一年级的学生进行了问卷调查，表2即为传统作业布置的相关调查结果.

从表2中不难看出，还是有很多学生比较不满足这种传统的作业布置形式，很多学生表示自己曾经抄袭过作业，能真正积极主动地完成作业的同学百分比不高，不能按时完成作业的学生大有人在，而相对的，很多学生表达了对分层作业的期待. 高一年级数学备课组根据学生调查问卷所得的结果进行了讨论和思考：（1）我校的学生在高中录取时的分数在我区是中上的，部分学生存在偏科现象，部分学生数学学习的基础薄弱，在进行数学学习的过程中往往会感到力不从心，在完成作业的过程中也会感到困难，因此，教师在布置作业时应能考虑到学生的认知和知识水平，在布置作业时，多一些考量与设计，尽量使得作业的难度和数量适应学生的能力水平. （2）不够合理的作业布置令很多学生的作业积极性大大降低，作业题量较大，题目类型重复率较高的问题将会使得学生在完成作业时只是机械地做题，对于学生来说是一种负担，教师在作业布置时应能够适当调整作业结构，让作业的难度层次更加明显，凸显出作业的价值，以促进学生数学学习的积极情绪的萌发.

[?]作业的分类设置

教师在深刻认识课堂教学价值的同时，也应能够对作业的功能形成正确的认知，事实上，数学作业的布置和课堂教学在数学教育教学中的地位是相同的，作业可以沟通课堂与课后，是学生自主学习的重要阶段，因此，教师在作业的考量、设计与布置时应多花心思以帮助不同能力水平的学生及时巩固知识.

1. 分层分类设置

根据学生接受能力和认知水平的高低将同一个问题设置成几种不同的方法或形式呈现给学生的作业布置方式，就是本文所指的分层分类设置. 比如，笔者在“圆与直线的位置关系”这一内容的作业布置上就设计了以下两种办法：①联立方程組，消去一个未知数并得到一个关于另一个未知数的一元二次方程，最后再利用方程的判别式对直线和圆的位置关系进行判断;②探寻圆心到直线的距离d和圆的半径r之间的大小关系并因此对直线和圆的位置关系进行判断. 同一道题的不同设问考查方式能够令学生的兴趣倍增，也可以使不同层次的学生在针对性的作业完成中均获得了能力的发展.

2. 组合设置

围绕某一重要知识点的巩固而设计的两种以上习题集合而成的作业设计即为作业的组合设置，这样的设计方式可以帮助学生在较少的题量中对更多的知识点进行巩固，使得题目更具有导向性，既丰富了题目的内涵，也增添了趣味性.

比如，笔者在“等差数列”的教学之后设计如下作业：

已知数列{an}的前n项和Sn=-n2+16n.

（1）求数列{an}的通项公式，并判断该数列是否为等差数列，说明理由;

（2）判断数列{an}是否为递减数列;

（3）求数列{an}的前n项和Sn的最大值;

（4）求数列{an}的前n项和Tn.

此题由4道基础题组合而来，每一个小问都能单独成题. 若将其分成4道独立的试题布置给学生课后完成，则会浪费学生的学习时间，使其做一些无用功. 加以整合后，思维训练内容不但没有减少，反而增加了思辨性，同时学生的学习负担也得以减轻.

3. 变式作业

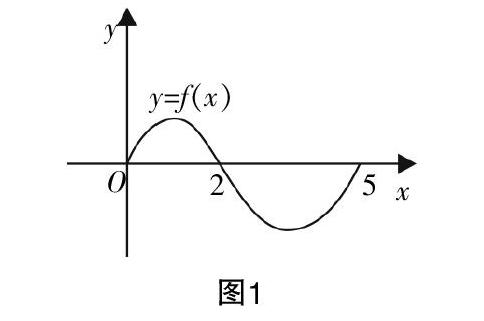
改变题目的部分条件并使原题改变成一道或几道与原题等值或不等值的题目即为我们通常所说的一题多变. 比如，设奇函数f（x）的定义域是[-5.5]，若当x∈[0，5]时，f（x）的图像如图1所示，则不等式f（x）<0的解为_______.

根据上述题目，我们至少可以有以下几种变式.

变式1：设奇函数f（x）的定义域是[-5，5]，若当x∈[0，5]时，f（x）的图像如图1所示，则不等式xf（x）<0的解为_____.

变式2：设偶函数f（x）的定义域是[-5，5]，若当x∈[0，5]时，f（x）的图像如图1所示，则不等式f（x）<0的解为_____.

学生可以在有意义的变式练习中意识到知识点与题目之间的关系，扩展了解题思路，对知识点的认知也会变得更加全面和深刻，往往能够获得“做一题、会一类”的学习效果.

[?]作业改革尝试

我校高一年级备课组以激发学生主动性为主题尝试了作业改革，一些典型、生动的高中数学作业新模式得到了很好的探索和实践，真正减轻学生作业负担的同时，更好地发挥了作业的价值，改善了之前存在的问题.

1. 自选作业

教师首先根据教学单元设计的目标和内容进行大量的作业设计，对学生提出作业完成的量的要求，要求学生在保障最低作业量的情况下自主选择作业进行练习，学生的大量作业因此转嫁成教师的大量作业设计，自选作业模式使得学生得以自主选择作业，大大地提升了学生作业的积极性，作业效果明显提升的同时也令不少学生感受到了作为作业主人的快乐[2].

2. 分层设置作业

在各單元教学结束之后进行“形成性测试”并根据测试成绩将学生分层，根据“合格”学生和“需努力”学生的分层进行A、B两种作业的设计，A种作业的题型一般都是选择题和一两道基础大题，更强调基础和结果，B种作业的题型一般为解答题，更强调逻辑和过程. “需努力”的学生完成作业A时必须独立自主，然后再将作业交给“合格”学生批改并及时纠错. “合格”学生完成作业B时必须有详细的解答过程并展示给“需努力”学生进行观摩和学习. 学生的作业负担有效减轻的同时也形成互相帮助的良好学风[3].

3. 自编作业

实际教学的过程中，由于学生能力水平的差异以及考试、学习要求的变化，市面上的作业题有时不能很好地契合学生的学习需求，教师在某一章节的教学结束之后应及时指导学生对需要巩固的知识进行重点关注，设计出能够将这些知识串联起来的作业并提供给学生练习，同时也可以转变思路，让学生自主编写题目. 比如，引导学生在例题“若f（x）在（0，+∞）上为增函数，则f（x）在（-∞，0）上也为增函数”进行题型的自主编写：

编写题目与自己完成作业不同，它更强调对知识点的整体认知，需要学生能够找出适合知识点的模型，也需要学生对于考纲有一个比较清晰的了解，可以说，自主编写题目的模式对学生的能力水平提出了新的需求，学生在这样的身份转变中得以从不同的角度去看待知识点，除此之外，这样的模式还更具有趣味性，能够调动学生自主探索与思考的积极性，引导学生充分地投入编题过程中，以此很好地帮助他们提升知识的运用能力. 教师还可以鼓励学生之间交换解题，对质量较高的题目进行分析和编录，这将有助于形成一种互相学习、积极探索的氛围，帮助学生爱上学习.

三种作业模式在我校学生的数学学习上也反馈出了具有一定差异的效果，因此，我们对作业设计与布置还会不断进行研究与改进，逐渐探索出更加适合学生学习和教师教学的作业布置模式，使作业形式更加人性化，更加贴合学生的认知特点，同时，我们还希望能够通过改变作业布置的形式，达到因材施教的效果，使得不同能力水平的学生都能在完成作业的过程中有所收获，使作业真正服务于教师的“教”和学生的“学”.

参考文献：

[1]  马复.试论数学理解的两种类型——从R.斯根普的工作谈起[J].数学教育学报，2001，10（3）：50-51.

[2]  黄艳玲，喻平. 对数学理解的再认识[J]. 数学教育学报，2002，11（3）：40.

[3]  黄梅，黄希庭. 知识的加工阶段与教学条件[J]. 教育研究，2015（7）：108-115.