均衡的完全3-部3-一致超图的单色放松路划分
李婷婷 张 霞
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
路划分问题起源于Gerencsér和Gyárfás[1](1967年)提出的一个基本的命题: 对于n个顶点的完全图Kn的任意的一个2-边染色, 它的顶点集V(Kn)可以被划分成一条红色路和一条蓝色路. 这里的空集和单点可以看作是染任意颜色的一条路. 1979年,Lehel猜想用圈代替上述命题中的路结论仍然成立. 对于n很大时Lehel猜想在文献[2]和[3]中被证实, 并且在2010年由Bessy和Thomassé[4]证得对所有的n都成立.
对于超图的情形, 本文先介绍论文中所用的一些基本概念和相关符号表示, 若未提及的概念和符号表示请参考文献[5]和[6].
一个k-一致超图H, 有l条超边e1,e2,e3,…,el满足对任意的i∈[l-1], 有|ei∩ei+1|=1并且对于2≤i+1 图G(或超图H)的一个边染色是从边集E(G)(或E(H))到颜色集的一个映射φ:E(G)→{1,2,3,…,k}(或E(H)). 上述称为图G(或超图H)的k种颜色的边染色, 简记为k-边染色. 本文主要讨论2-边染色, 一般用红色和蓝色来叙述. 2013年, Gyárfás和Sárközy[7]提出了一个关于完全的3-一致超图的单色划分的问题. 2018年,Bustamante, Hán和Stein证得下面的引理1. 值得注意的是对于放松圈(loose cycle)上述结论同样成立. 另外,引理1中ηn可以被改进. 目前对于完全超图的边染色的单色划分的研究结果相对较少, 对于完全的k-部k-一致超图的边染色的单色划分问题还没有相关的结果, 完全的k-部k-一致超图相对于完全超图研究起来更复杂, 对边的要求更苛刻. 本文研究均衡的完全3-部3-一致超图的单色放松路的划分, 为以后研究一般的k-部k-一致超图的单色划分问题打下基础. 证s≤2时,结论显然成立. 下面讨论s≥3的情况. 在以下证明中,顶点的下标是指该点所属的超图的部,比如意味着w2∈V2. 证因为|W|≥s+1,PR和PB最多能够覆盖2s-1个点. 考虑两种情况. 性质2PR和PB都是正常的放松路. 2) |V(PR)|=2t+1,其中整数t≥2, 即PR包含至少2条超边.PR为{v1,v2,v3}中的某个点, 注意V(PB)={u2,u3},令集合V=ev={vi,vj}(其中i≠j,i,j∈{1,2,3}).由情形1)知超边viwjwk,vjwiwk(其中i,j,k∈{1,2,3},i≠j≠k)为染蓝色,则PR′=PRe和PB′={viwjwk}∪{wkwivj}与假设矛盾,故综上所述得放松路PB是正常的. 此时可知两条放松路PR,PB均为正常的路, 且很容易得其中放松路PR至少有2条超边,否则PR={v1,v2,v3}且PB={u1,u2,u3},类似性质2中的情形1)知超边viwjwk(其中i,j,k∈{1,2,3},i≠j≠k)为染蓝色,超边uiwjwk(其中i,j,k∈{1,2,3},i≠j≠k)为染红色. 由对称性不妨设u2v3w1为红色,则PR′=PR∪{v3u2w1}∪{w1u3w2}∪{w2u1w3}与假设|V(PR)|+|V(PB)|是最大矛盾. 下面我们令放松路PR的第一条超边为f={x1,x2,x3}, 最后一条超边为e={v1,v2,v3}; 令放松路PB的最后一条超边为g={u1,u2,u3}. 对于超边f,e,g中的二度点分别为x,v,u它们分别是{x1,x2,x3}, {v1,v2,v3}, {u1,u2,u3}中的某个点, 令集合X=fx,V=ev,U=gu分别表示超边f,e,g中去掉二度点以外的点的集合; 取W′⊆W, 且W′={w1,w2,w3}. 其中X,V是对称的,从而对于X,V,U的所有可能的随机组合,我们可以分为两种情形进行具体讨论. 情形1:存在超边e″={xi,vj,uk}, 其中xi∈X,vj∈V,uk∈U,且i,j,k∈{1,2,3},i≠j≠k. 由超边e″={xi,vj,uk}知Xxi=xj或xk,Vvj=vi或vk,Uuk=ui或uj,这里我们只证明其中一种,其他可类似得证. 考虑Xxi=xj,Vvj=vi,Uuk=ui,由已知超边viwjwk,vjwiwk为蓝色,超边uiwjwk,ukwiwj为红色. 下面讨论超边e″,如果超边e″为染红色, 则PR′=PRf∪e″∪{ukwiwj}∪{wjuiwk}和PB′=PBg(当放松路PB恰有一条边时,PB′={vi,uj})与假设|V(PR)|+|V(PB)|是最大矛盾. 如果超边e″为染蓝色, 则新的放松路PR′=PR{f,e}(当放松路PR恰有两条超边时,PR′={xj,vk})和PB′=PB∪e″∪{vjwiwk}∪{wkwjvi}与假设|V(PR)|+|V(PB)|是最大矛盾. 情形2:不存在超边e″={xi,vj,uk}, 其中xi∈X,vj∈V,uk∈U,且i,j,k∈{1,2,3},i≠j≠k. 我们讨论了关于均衡的完全3-部3-一致超图的任意2-边染色的单色放松路的划分问题, 那么有没有其他的工具使关于均衡的完全3-部3-一致超图的单色划分问题得到更好的结果? 对于均衡的完全k-部k-一致超图的任意r-边染色的单色划分问题呢? 因此, 我们有以下两个可以进一步研究的问题. 问题2对于均衡的完全3-部3-一致超图的任意的2-边染色, 至少存在多少条点不交的单色放松路能够将该超图的所有点全部覆盖? 问题3对于均衡的完全k-部k-一致超图的任意的r-边染色(r≥2),存在多少个点不交的单色放松路或单色放松圈能够将该超图的所有点全部覆盖?


2 结论及其证明

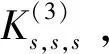
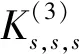
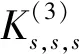
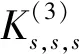


3 可进一步研究的问题

