基于三次样条趋势滤波和知识 指导的大规模不等长时序族聚类

冀东丽

( 山东特殊教育职业学院，250022，济南 )

1 引 言

时间序列是指在一定的时间间隔内所记录的一系列具有时间意义的序列数据，在金融、经济、气象、通信工程、医疗卫生等领域有着广泛的应用.从大量时序数据中挖掘潜在的信息和模式，是数据挖掘领域中最具挑战性的大问题之一[1]，而聚类分析能有效挖掘数据中的重要信息，是数据挖掘中的重要任务之一.在实际问题中，由于时间段的数据丢失及数据保密性等，会导致遇到的时序数据族并不等长，因此开展大规模不等长时序数据族的智能聚类研究更具有现实意义.

目前智能聚类研究主要包括两个方面：一是由于数据族中各数据长度不一致，即包含的数据点的个数不相同，因此如何度量任意两数据之间的相似关系便成为首要解决的问题.常用的欧氏距离能够快速实现对两个等长时间序列的距离度量，但对于不等长时间序列却无能为力，因此，常通过动态时间扭曲方法(dynamic time warping, DTW)[2-4]实现不等长序列的最佳匹配.由于DTW算法时间较长，大量研究主要集中在提高DTW的时间性能上[5-9].这些方法虽然能提高时间效率，但往往以牺牲时间特征为代价，聚类结果不够理想.另一方面，涌现了大量关于时间序列形态的研究，通过各种方式度量时间序列之间的相似性，比如Keogh的分段线性表示[10]，Hung的分段聚合近似[11]，Lin的符号化表示[12]，Chan的离散小波[13]，Agrawa的离散傅里叶变换[14]及Fuchs的多项式回归分析[15]等.这些方法的共同之处是虽然注意了时间序列的形态特征，但都是只侧重于数值轴的信息，并没有完全反映时间轴的信息.

摆在我们面前的一个问题就是如何引入能同时体现时间轴和数值轴信息的新度量方法，让时间序列动态特性得到充分体现的同时，还能准确度量距离，在时间效率上也能得到保障.目前这方面的研究较少，文献[16]中首次引入基于线段面积的度量方式，但该方法对于由光滑曲线产生的时间序列，聚类效果较差.基于以上原因，本文提出基于三次样条规则化的改进的动态时间规整算法(SPDTW)，并将该算法与知识指导相结合，应用于大规模不等长时间数据族的聚类问题中.全文共分为四部分：第一部分借助三次样条规则化滤波，将原始时间序列用三次样条近似表示，找出反映时间序列趋势的关键点；第二部分定义任意两时间序列之间的距离，这是对于大规模不等长时间数据聚类的关键.首先考虑任意两曲线段的趋势差异，利用函数的导数构造曲线段间的距离，从而得到一个距离矩阵，利用动态时间规整算法在距离矩阵上寻找最优路径，得到最终的累积距离作为两个不等长时间序列之间的距离；第三部分基于SPDTW和知识指导的聚类过程.将大规模不等长时间序列分成若干部分，通过SPDTW得到各部分的距离矩阵，利用最大树法得到各部分子序列族的聚类结果，统计任意两个时间序列出现在同一类中的次数，得到一个对称矩阵，通过归一化处理，得到相似矩阵，再次利用最大树法得到最终聚类结果；最后一部分是以仿真实验来验证算法的有效性及时间效率.

2 三次样条规则化趋势滤波

目前有很多关于趋势滤波的算法，例如Hodrick-Precott(H-P)滤波[17],l1趋势滤波[18],l1规则化趋势滤波[19]，l2规则化趋势滤波[19]，移动平均滤波[20]等，这些方法在数据挖掘中起了重要的作用，但每种滤波方式都有一定局限性.例如：l1和H-P趋势滤波对原始数据呈线性且比较平滑的情况，滤波后得到的趋势与原数据相似性较好，但对于一些特殊异常值的处理不如谢邦昌等提出的l1和l2规则化趋势滤波[19]效果好.但是如果原始数据对应的函数是非常光滑的，谢提出的方法得到的趋势整体误差较大，且在连接点处的光滑性难以保证.指数滤波解决了光滑性的问题[21]，但在很多情况下，曲线并不是指数形的，而是具有波动性.Christian H. Reinsch分别在文献[22]和文献[23]中讨论了三次和高次样条函数的光滑性，为我们提供了一种滤波的算法，但他们均未对异常值进行处理.受Christian H. Reinsch和Huber[24]的启发，鉴于三次样条比k(k>3)次样条计算量小这一原因，本文给出三次样条规则化趋势滤波算法，该方法既能保证挖掘的数据关键点与原始数据在趋势上有较高的吻合度，又可以解决最小二乘损失函数对异常值的干扰，可以得到稳健的趋势估计.

假设时间序列y=(y1,…,yi,…,yn)包含一个基本趋势x=(x1,…,xi,…,xn)和随机成分z=(z1,…,zi,…,zn)，其中yi=y(ti),xi=x(ti),zi=z(ti)，y(t),x(t),z(t)都是时间t的函数，ti是时间采样点.本文假设时间序列y有有限个异常值，它是由几乎处处光滑的函数生成的.不失一般性，不妨假设只有一个异常值，记为yi0=y(ti0)，且异常值不出现在两个端点处，否则在众多的数据点中删除该异常值点.若有多个异常值，则将全体数据分割成若干部分，使得每个部分包含一个异常值，然后按相同的方式进行处理.

我们的目的是挖掘趋势信息x，一方面希望x和y尽可能有相同的趋势，另一方面希望随机成分(残差或者波动项)尽可能小，同时减少异常值的干扰.提出如下优化问题：

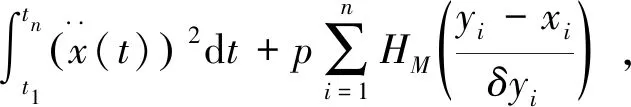
(1)

其中积分项反映的是趋势的光滑性，第二项求和反映的是原始时间序列与基本趋势之间的误差，p是一个非负参数，用来控制光滑性和残差在优化问题中的权重.

下面分别对x(t)和HM(u)进行说明：

1)y1=x1,yn=xn.

(2)

2) 对于任意的时间点ti(i=2,…,n-1)，

x(k)(ti)-=x(k)(ti)+,k=0,1,2，

(3)

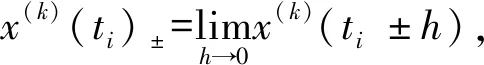
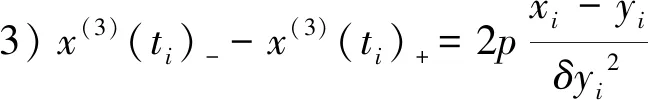
(4)

4) 规定x(4)(t)=0.

从以上假设可知x(t)是[t1,tn]上的三次样条函数[22].

(5)

6)M是一个给定的参数，用来控制数据中异常值对趋势估计的影响，它描述了损失函数HM(u)从二次函数变为线性函数的过渡点.Hubert建议当残差服从正态分布时，M取1.345可以在保证95%统计效率的前提下，得到尽量多的稳健性[24].

7)δyi>0(i=1,…,n)是残差的分布参数，通常可取原始时间序列的标准方差.

(6)

由于x(t)是三次样条函数，设第i段的三次多项式的形式为

xi(t)=ai+bi(t-ti)+ci(t-ti)2+di(t-ti)3(i=1,…,n-1).

(7)

(8)

根据(2)、(4)及(8)式，I可写成如下形式：

(9)

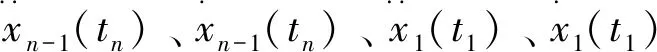
令H=H4H3-H2H1，根据上述四式容易计算J≈xAxT.将J≈xAxT及(9)式代入(1)式，得到一个 (1)式近似的优化问题：

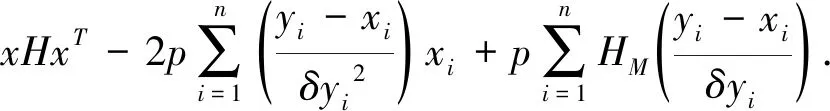
(10)

(11)

(12)

由最小二乘法知(12)式目标函数中的最优解形式为

(13)

从(13)式可看出，当p→时，x→y.通过解优化问题，可以得到原始时间序列的关键点xi(i=1,…,n),利用Hermite插值或者三弯矩法可以得到三次样条函数xi(t)，(t∈[ti,ti+1] ，i=1,…,n-1).将xi(t)的4个系数(ai,bi,ci,di)作为列向量存储在矩阵B4×(n-1)中.

3 两时间序列之间的距离

3.1曲线段间的距离度量设f(t)和g(t)是区间[t′,t″]上的两条函数.现给出它们间的距离度量规则.

1)f(t)和g(t)信息完整且趋势相同(如图1所示).

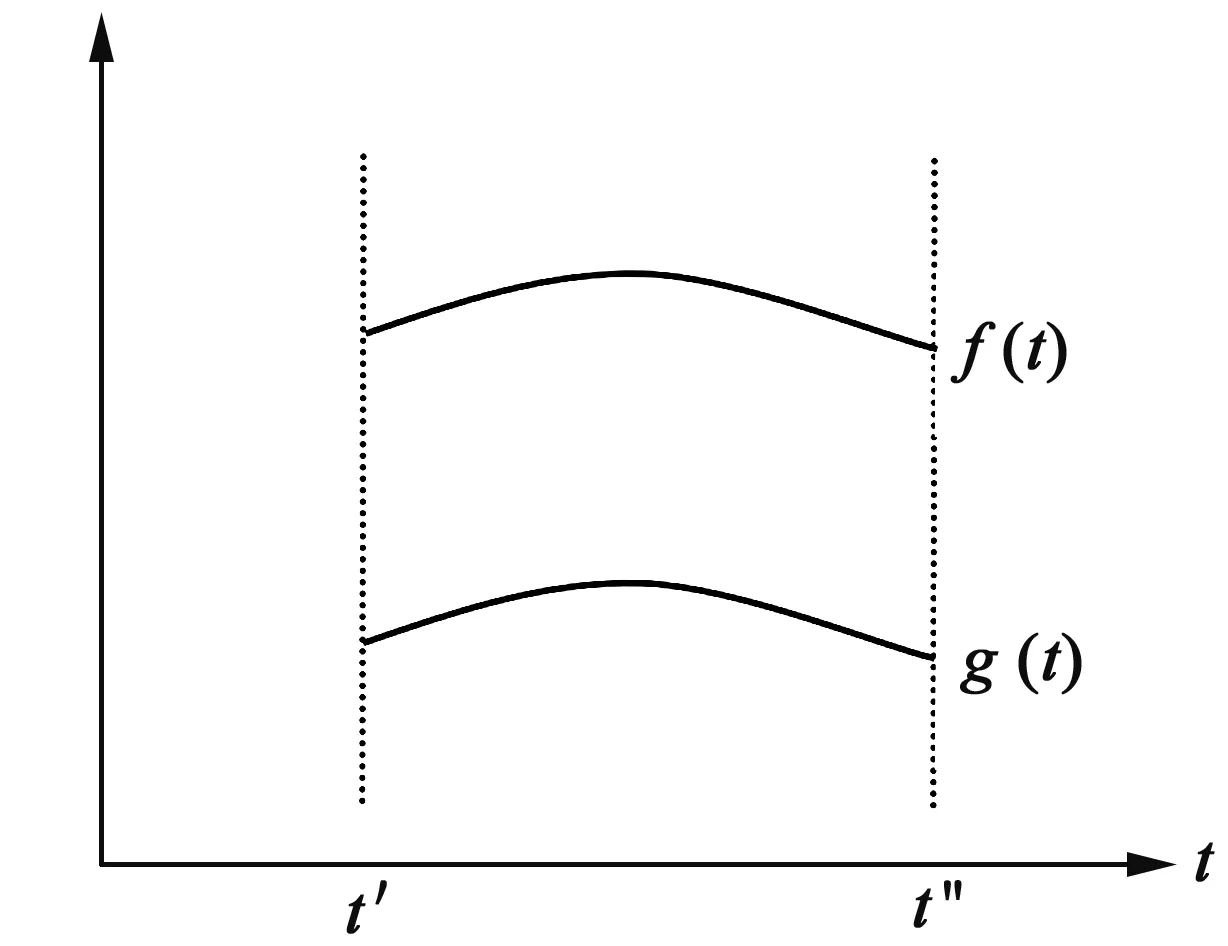
图1 f(t)和g(t)信息完整且趋势相同

图2 f(t)和g(t)信息完整但趋势不同

2)f(t)和g(t)信息完整但趋势不同(如图2所示).

不存在常数c，使得f(t)=g(t)+c，此时各点之间的趋势差异仍可用变化率来表示，因此对于这种情况定义

(14)

可见1)是2)的特殊情况.若f(t)和g(t)是三次多项式，即

f(t)=af+bf(t-t')+cf(t-t')2+df(t-t')3，

g(t)=ag+bg(t-t')+cg(t-t′)2+dg(t-t′)3，

(15)

3)f(t)和g(t)信息不完整且趋势不同(如图3-图6所示).

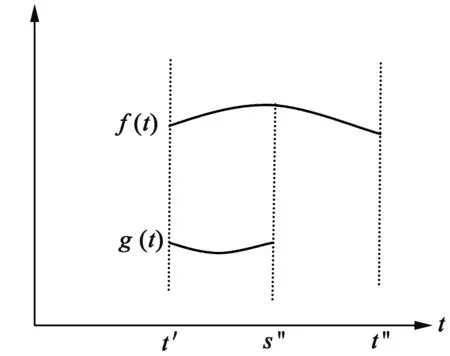
图3 f(t)信息完整，g(t)后续信息不完整且趋势不同

图4 f(t)信息完整，g(t)前部信息不完整且趋势不同

图5 f(t)信息完整，g(t)前后信息均不完整且趋势不同

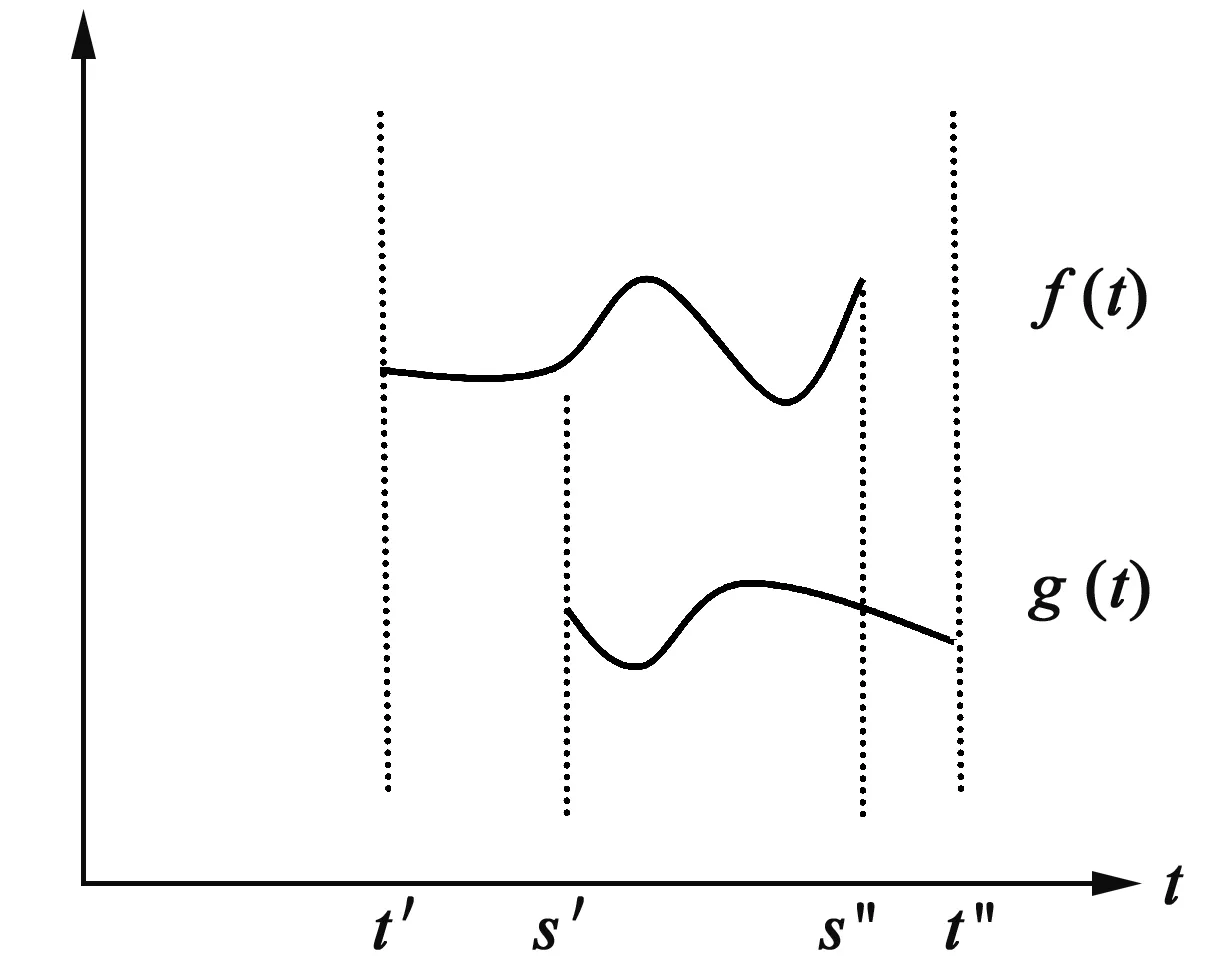
图6 f(t)和g(t)信息均不完整且趋势不同

图3-图5以及两条曲线段不在同一时间段的情形均可利用图6的处理方式来定义距离.因此本文主要考虑图6的定义规则.对于区间[s',s'']中的趋势差异仍可用(14)的公式进行度量，即

(16)

对于[t',s']∪[s″,t″]这部分，只有一个函数的信息可用.在这部分，两个函数之间的差异既有时间和数值上的差异，又有趋势变化的差异.综合考虑，可用这三种信息的加权平均来反映两条函数的差异.定义

(17)

来表示信息不全的部分的距离，其中αi(i=1,2,3,4)是各项的权重.到此为止，任意两个曲线段之间的距离度量公式可表示为

d(f,g)=dcom(f,g)+dincom(f,g).

(18)

3.2基于三次样条规则化的动态时间规整算法(SPDTW)

步骤1预处理(Spline规则化趋势滤波).

步骤2求三次样条函数.

利用所获关键点求出三次样条函数，用分段三次多项式近似表示原始时间序列.

步骤3计算任意两个曲线段间的距离.

利用(17)式计算任意时间段里两曲线段之间的距离，得到一个K1×K2距离矩阵.

步骤4计算原始时间序列X和Y之间的距离.

运用动态时间规整算法,在距离矩阵上寻找最优路径

W=c1,…,ck,…,cK，max(K1,K2)≤K

k表示路径的长度，并得到最终的累积距离作为不等长时间序列X和Y之间的距离.

动态时间规整算法搜索的约束条件为:

1) 端点约束：搜索路径的起始点和终止点正好位于两个时间序列的两个端点，即

c1=(1,1)，ck=(K1,K2)；

2) 局部连续约束：路径W中的点在时间上不能后退，且每一个弯折步必须彼此相邻(包括对角线元素)，即ck=(a,b),ck-1=(a',b') 0≤a-a'≤1,0≤b-b'≤1.动态时间规整采用递推和迭代的方法发现最短距离

(19)

下面通过动态规划的方法找到最短路径，即

(20)

最终时间序列弯曲路径最小累加值W(m,n)为时间序列X和Y的动态弯曲距离.

4 基于SPDTW和知识指导的大规模不等长时序族的聚类

4.1问题描述N条不等长的时间序列X1,…,XN组成时间序列族，时间序列Xi可表示为

4.2聚类过程对每个子序列族Partq，应用SPDTW算法，得到一个Nq×Nq对称距离矩阵

统计任意Xi和Xj(i,j=1,…,N)在每个Partq中出现在同一类的次数并求和，记

其中,

从而得到一个N×N的对称矩阵R'，其主对角线上的元素均为N.对R'进行归一化处理，令

得到一个N×N的相似矩阵R，R中对角线元素全为1且R(i,j)∈[0,1].再次利用Prim方法构造最大树，即可得到不同阈值下的最终的清晰化的聚类结果.

5 仿真实验

5.1数据来源首先利用函数35sin(|t|)、25sin(t)、25cos(t)分别在[-400,300]、[-600,380]、[-200,500]以Δt=0.4为间隔生成三支不等长的时间序列X、Y、Z，长度分别为nX=1 751，nY=2 451，nZ=1 751.然后给出三组人造时序数据族，构造方式如下：

经过如此构造，得到由X、Y、Z及人造时间序列XN、YN、ZN构成的一族聚类对象.为方便起见，分别用{X1,X2,X3,X4,X5}，{X6,X7,X8,X9,X10}和{X11,X12,X13,X14,X15}标记{XN1,XN2,NX3,NX4,X}，{YN1,YN2,YX3,YX4,Y}和{ZN1,ZN2,ZX3,ZX4,Z}.

5.2SPDTW和IDTW的比较为了更好展现SPDTW和IDTW的差别，先将IDTW的主要方法和步骤列出来.

1) 关键点的选取(l1趋势滤波).

利用如下优化问题

得到时间序列y=(y1,…,yi,…,yn)的基本趋势x=(x1,…,xi,…,xn).

2) 利用分段直线近似表示原始时间序列.

4) 利用动态时间规整算法计算X和Y的最终距离.

5) 聚类过程.

由于每个Partq中所含数据的条数不相同，因此各个Partq对应的相似矩阵Rq的阶数也不相同，为了将所有数据最终用一个矩阵表示它们的相似关系，IDTW先找出一个阶数最大的矩阵(为了方便叙述，假设最后一段阶数最大)，然后利用

依次从后向前将每个Rq都补成与RQ相同阶数的矩阵，再利用

得到所有数据族的相似矩阵，最后利用传递闭包进行聚类.

下面通过仿真实验说明二者的差别.对于上述时间序列族，分别用本文给出的方法与基于IDTW和知识指导的聚类算法就聚类结果及时间耗费进行对比，对比结果分别列于表1和表2中.为了书写方便，表1中数字1～15分别代表数据族中的时间序列X1～X15.

表1 SPDTW和IDTW聚类结果

表1结果表明：针对不等长时间序列族聚类问题，基于SPDTW和知识指导的聚类算法得到了预想的结果.5,10,15是数据族中的基本数列，不存在随机性，而{1,2,34}，{6,7,8,9}和{11,12,13,14}分别是5,10,15通过加入随机数并平移得到的，因此在趋势上具有很大的相似性，因此在λ=0.994 5时，就相应地聚为一类.而IDTW的聚类结果并不理想，在λ较小时，也没能将趋势相同的数据聚为一类.这是因为IDTW虽然考虑了时间轴和数值轴的分布，但它是用折线段近似代替原始时间序列，这样不能保证光滑性，且误差大.此外在聚类过程中，文献[16]中用最后一部分PartN的相似矩阵的元素扩充PartN-1对应的相似矩阵中缺少的元素，按照这方式一直向前推，直到推到Part1对应的相似矩阵.这种处理方式，主要的思想是用近期的数据推算之前的信息，作为短期的推测，得到的效果比较好，但若时间段很长，得到的趋势差别就会很大.

本文没有将各个部分的相似矩阵扩充成阶数相同的矩阵，而是直接在每个部分聚类，统计出任意两个时间序列出现在同一类的次数，最后综合考虑聚类结果，从而避免了对未出现的时间序列补充过多的不确定的信息，提高了聚类结果的准确性.

5.3效率对比对于大规模时间序列的聚类算法，时间效率是一项重要的测试指标.基于SPDTW和知识指导的聚类算法包括三大部分：第一部分是每个Partq中三次样条函数规则化趋势滤波过程；第二部分是SPDTW距离度量过程；第三部分是知识指导聚类过程(统计频数，生成最大树，聚类).我们将基于SPDTW和知识指导的聚类算法及基于IDTW和知识指导的聚类算法所用时间进行对比，结果见表2.“s”表示时间，单位：s.

表2 SPDTW和IDTW聚类时间消耗对比

表2表明：与基于IDTW和知识指导的聚类算法相比，基于SPDTW和知识指导的聚类算法在时间消耗上没有太大差别，IDTW方法在数据拟合时，时间要优于SPDTW，这是因为后者涉及三次多项式的四个系数存储及运算，而前者在计算距离时只用到关键点的坐标，这在第一步滤波时就已得到.但在其他方面时间相差不多.在动态寻优过程中SPDTW还略快于IDTW.计算整个过程的总时间，二者几乎相等.

6 结 论

在文献[16]中已经验证IDTW与传统的DTW相比，无论在聚类结果还是时间效率上都有很大的优势，而SPDTW对于光滑曲线产生的数据在聚类上优于IDTW.由此看见本文提出的方法对于解决大规模不等长时间序列的聚类问题有一定的作用.但从表2中也可以看出，时间消耗主要集中在DWT寻找最短路径上，因此本文提出的方法还有改进的余地.主要可从以下两方面考虑，一是改进路径的寻优过程；二是给出两时间序列动态弯曲距离的其他形式的计算公式.利用DTW寻找最短路径的原因是两个不等长的时间序列无法逐段比较趋势变化，所以可从这点出发，将不等长时间序列改造成能够逐段比较的两个等价的对象.