一道三角形面积最大值问题解法赏析

湖北省阳新县高级中学

邹生书 (邮编：435200)

题目已知△ABC是以AC为斜边的等腰直角三角形，D为△ABC外一点，且CD=2AD=2，则△BCD面积的最大值为.

这是衡水金卷2019届高三理科数学(一)的第16题，是填空题的最后一题，是填空题中的压轴题，是一道得分率较低的题.难点是考生在紧张和有限的时间内很找到较好的解题思路和简单的解法，下面笔者提供几种解法与读者分享.

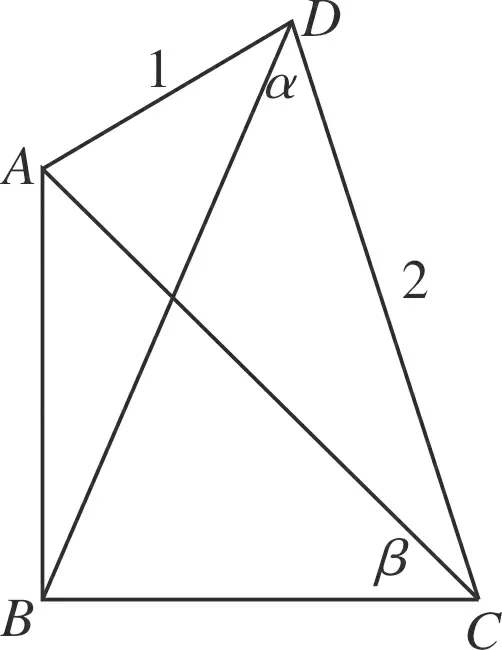
图1

解法1 (金卷给出的三角解法)

如图1，设∠ADC=α,∠ACD=β.

在△ACD中，由余弦定理得

AC2=12+22-2·1·2cosα=5-4cosα,

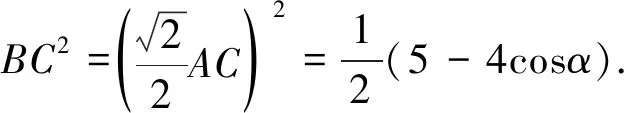
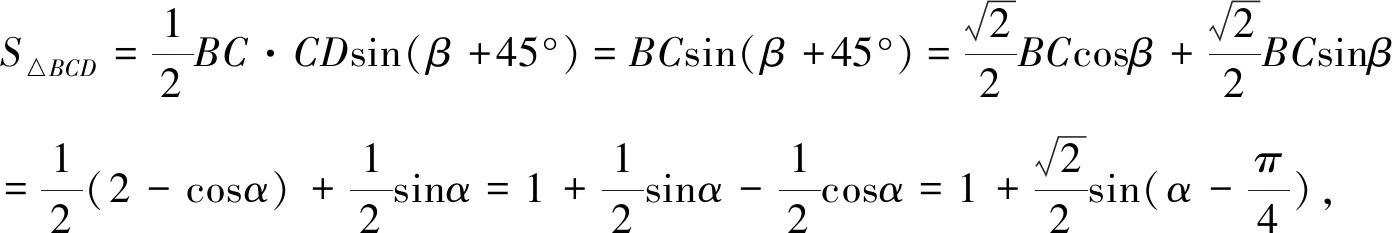
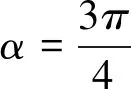
点评该解法主要用到了正定理和余弦定理及三角函数辅助角公式，但三角变形多而杂，显得小题大做不符合小题巧做的解题原则.

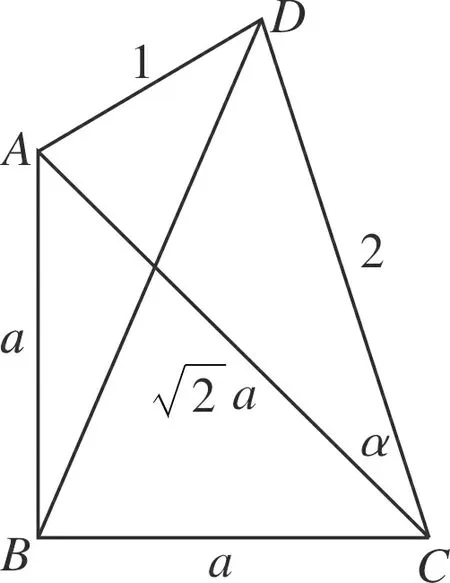
图2

解法2 (用同角三角函数的平方关系求解)

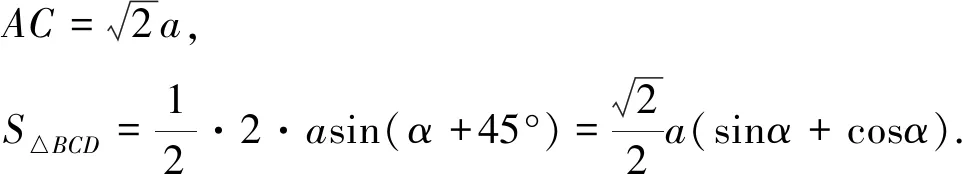
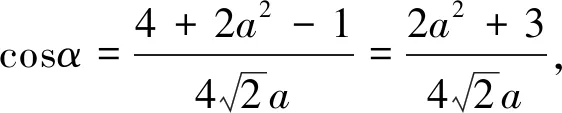
点评该解法思路虽清晰，但运算量大，感觉不够理想.

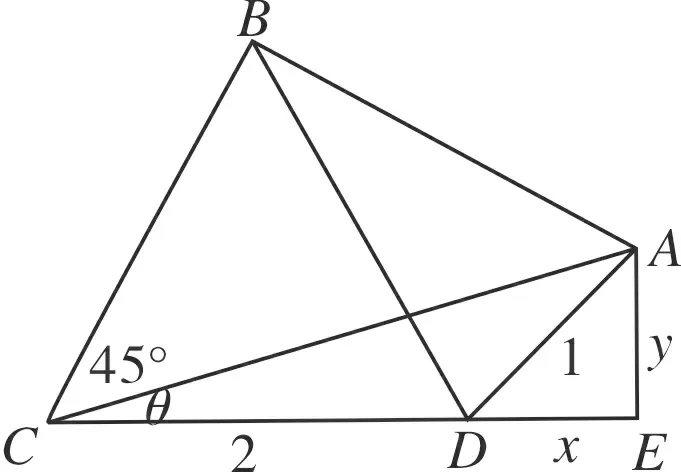
图3

解法3 (用均值不等式或柯西不等式求解)

如图3，作AE⊥CD于点E，设DE=x,AE=y，则x2+y2=1，设∠ACD=θ.

评注该解法中图形的放置与表现对解题思路影响较大，起着导向作用.本解法小题巧做易被学生接受，应该是本题的较理想的解法.把难题变得容易，把复杂的问题变得简单，数学最终是简单.

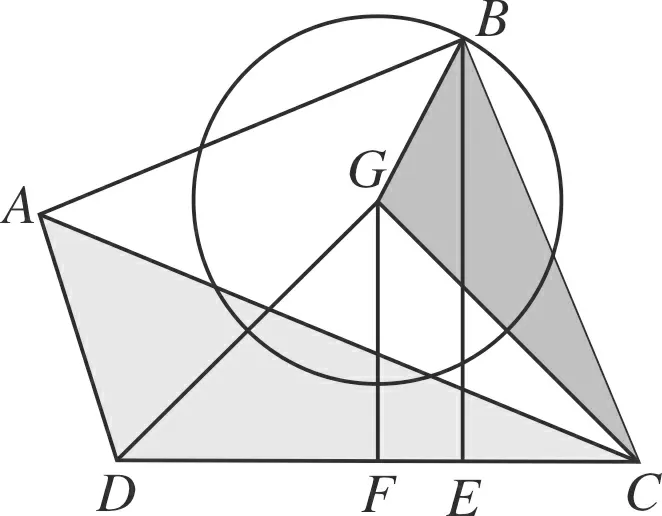
图4

解法4 (作等腰直角三角形证相似求解)

当且仅当B,G,F三点共线，且点G在线段

BE上时等号成立.

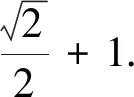
解法5 (用旋转伸缩变换求解)

图5

解法6 (用托勒密不等式求解，谢伦驾提供)

如图5,分别取AC,CD的中点H,O,

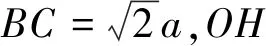
在四边形HBCO中，由托勒密不等式得

BO·HC≤BH·OD+BC·HO,

点评上述解法充分利用四边形托勒密不等式及垂线段最短二次放缩求三角形面积最大值.高观点低运算，解法高雅优美，很有品味.

托勒密不等式凸四边形的两组对边乘积和不小于其对角线的乘积，取等号当且仅当四边形共圆.

注本文参考了华师一附中退休教师郑用珂、广州市执信中学朱清波老师和湖南娄底市第一中学谢伦驾老师，在本人创建的公众号“邹生书数学”中推出文章中的解法，在此向他们表示感谢！