一道高考题的“昨天·今天·明天”—关于常态二次圆锥曲线定点(定向)问题解法的“融合”与应用

江苏省灌南中等专业学校(222500) 周如俊

高中数学教学研究类杂志每年都在高考之后,会对一些高考数学试题解法研究以专栏的形式呈现,吸引更多的教师关注、学习、研究与拓展,从而增强期刊内容的深度和力度.本文以一道高考题圆锥曲线定点(定向)问题解法为例,对有关期刊发表的研究论文进行梳理、溯源、整合,并对定点问题解法进行“融合”与“拓展”.

一、试题的溯源

(1)求C的方程;

(2)设直线l不经过P2且与C相交于A,B两点.若直线P2A与P2B直线的斜率的和为-1,证明l过定点.

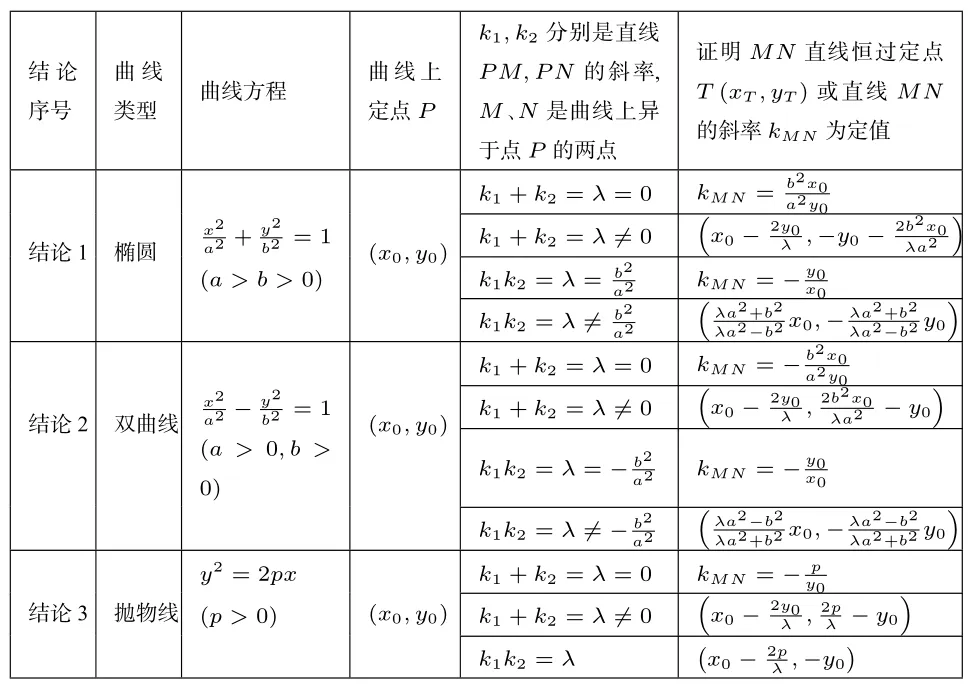
表1

查阅有关文献,上述高考题最早可能起源于文献[1-2],是在文献[3]相关结论基础上进行组题与命题的(如表1).由文献[3]有关结论简解如下:k1+k2=-1/=0,则直线l恒过定点,即T(2,-1).

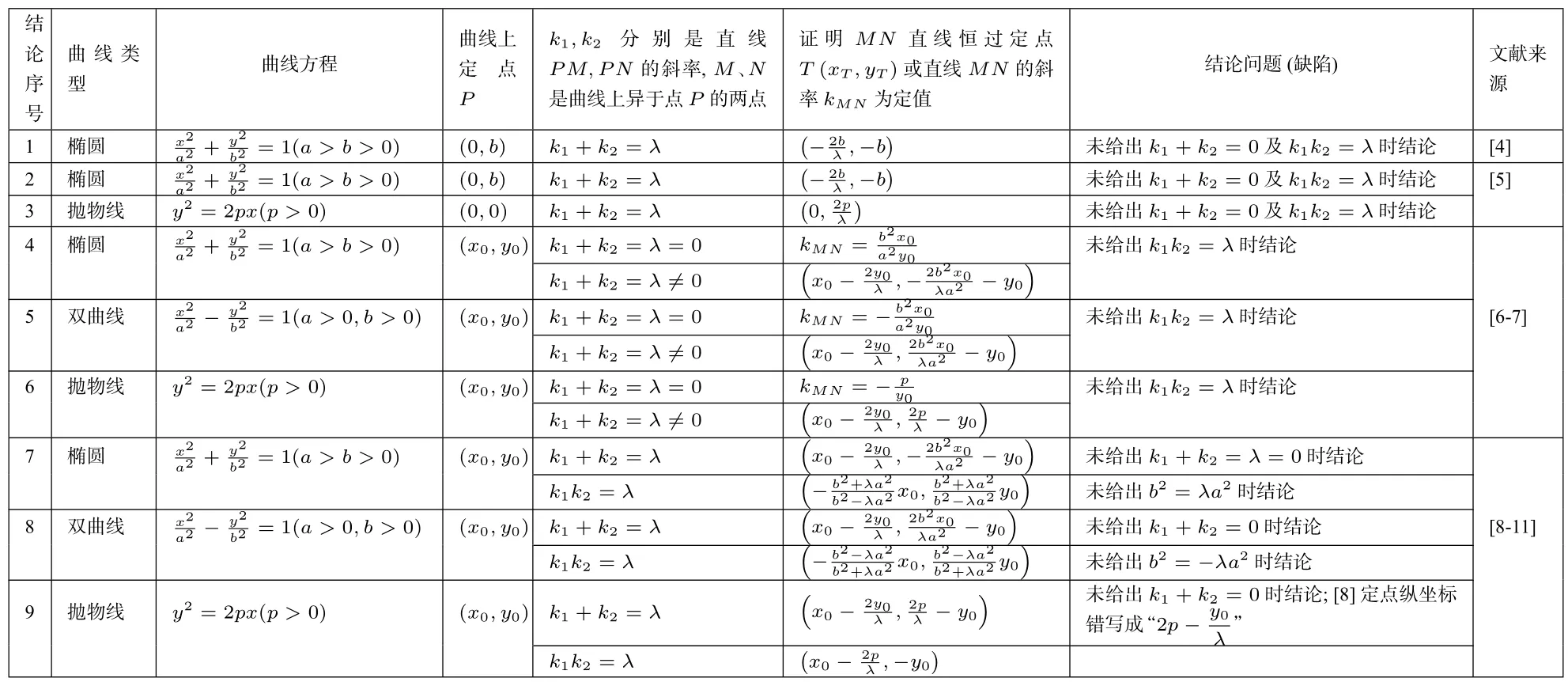
表2

阅读近三年有关高中数学教学研究类杂志,大都对上述高考题第(2)问的解法作了专题探究与一般性推广,有关研究结论归类如表2所示.表2呈出的有关结论的推导过程繁杂,表达式形式不一,相互间关联度低,识记难,缺失适用于圆、椭圆、双曲线、抛物线等常态二次圆锥曲线“通法”的求解公式.有的公式或遗漏相关参数,或公式结果有误,或缺失对特殊情况的结果研究.

此外,文[12]虽提出如下两个“试试”的结论,但没有给出证明过程,且该文的“结论1”有误.

结论1定点P(x0,y0)是二次曲线C:Ax2+By2+Cx+Dy+E=0上的一定点P(x0,y0),点M,N是二次曲线C上异于P点的两点,已知直线PM,PN的斜率kPM,kPN满足条件:kPM+kPN=λ(λ为常数,且λ/=0),则直线过定点.

结论2定点P(x0,y0)是二次曲线C:Ax2+By2+Cx+Dy+E=0上的一定点P(x0,y0),点M,N是二次曲线C上异于P点的两点,已知直线PM,PN的斜率kPM,kPN满足条件:kPMkPN=λ(λ为常数,且A-λB/=0),则直线过定点.

笔者尝试融合表1、表2“一般性结论”及文[12]的两个结论,形成圆、椭圆、双曲线、抛物线等常态二次圆锥曲线上动弦定点(定向)问题的“通法”的公式,具有简捷性、普适性、通用性,实现了多类归一、举一反三、触类旁通的教学效果.

二、解法的融合

综观表1、表2各类研究结论及文[12]的两个结论,都可以归结常态二次圆锥曲线(圆、椭圆、双曲线、抛物线)的定点(定向)问题:曲线上一定点P(x0,y0)引出的两条弦PM,PN,其两弦斜率kPM、kPN满足(kPM+kPN)或kPMkPN为定值,则动弦MN恒过定点或kMN为定值.本文将常见的圆、椭圆、双曲线、抛物线等常态二次圆锥曲线(方程统一为F)(x,y)=Ax2+By2+Cx+Dy+E=0A2+B2/=0,进行整合思考.为简化运算推论过程,形成如下解题思想:(1)坐标平移.将原点移到定点P(x0,y0),使得PM,PN均变为过新原点的直线(并设平移后直线M′N′方程为:mx′+ny′=1,构建关于(y-y0)和(x-x0)的齐二次方程,进而得到关于为元的一元二次方程;(2)运用韦达定理求定点(定值).(kPM+kPN)与kPMkPN分别是上述一元二次方程二根之和与之积,代入求解,推导关于m,n的关系的一次方程,联立mx′+ny′=1,求定点(定方向).为此得出如下两个定理.

定理1常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2/=0)上有一定点P(x0,y0)与异于P点的两动点M,N.已知直线PM,PN的斜率kPM,kPN满足条件:则有:

(1)若λB=0,则直线MN有定向,即kMN=(当F2=2By0+D=0时,直线MN⊥轴);

定理2常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2/=0)上有一定点P(x0,y0)与异于P点的两动点M,N.已知直线PM,PN的斜率kPM,kPN满足条件:kPMkPN=λ.记则有:

(1)若A-λB=0,则直线MN有定向,即kMN=(当F1=2Bx0+C=0时,直线MN⊥轴);

(2)若A-λB/=0,则直线MN恒过定点.

定理1、定理2简证如下:

证明作直线平移:代入F(x,y)=0,得:Ax′2+By′2+(2Ax0+C)x′+(2By0+D)y′=Ax′2+By′2+F1x′+F2y′=0.设平移后直线M′N′方程为:mx′+ny′=1,则有:Ax′2+By′2+(F1x′+F2y′)(mx′+ny′)=0,方程两根,故有:.

(I)证明定理1.

(1)若λB=0,则,直线MN有定向,即(当F=2By20+D=0时,直线MN⊥轴).

(2)若λB/=0,则有1.即直线M′N′方程mx′+ny′=1在x′O′y′中恒过定点,故直线MN在xOy中恒过定点.

(II)证明定理2

(1)若A-λB=0,则,直线MN有定向,即(当F1=2Bx0+C=0时,直线MN⊥轴).

(2)若A-λB/=0,则有即直线M′N′方程mx′+ny′=1在x′O′y′中恒过定点.故直线MN在xOy中恒过定点

上述证明步步可逆,故定理1、定理2逆命题均成立.

应用定理1、定理2对文[12]两个结论进行论证与校核:

若kPM+kPN=λ(λ为常数,λB/=0),则直线MN恒过定点

故文[12]中结论1“试试”结论有误,定点横、纵坐标表达式“分母”中“λ”应为“λB”.

若kPMkPN=λ(λ为常数,A-λB/=0),则直线MN恒过定点.文[12]中结论2正确.

应用定理1、定理2对表2相关结论作简证,限于篇幅证明略.

三、通解的应用

1.求证(解)恒过定点

例1(2017年高考全国卷I理科第20题)(题目见文首)

解析利用定理1简证上述高考题第(2)问:A=,B=1,F1=0,F2=2,直线AB在xOy中恒过定点,即恒过点T(2,-1).

2.求证(解)斜率为定值

例2(2004年高考北京卷理科第17题)如图1,过抛物线y2=2px(p＞0)上一定点P(x0,y0)(y0＞0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).

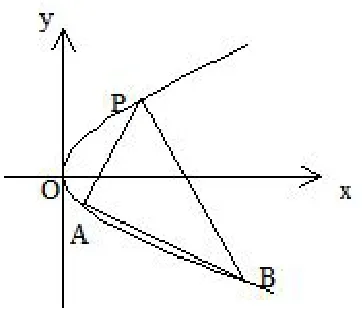
图1

(I)略.(II)当PA与PB的斜率存在且倾斜角互补时,证明直线AB的斜率是非零常数.

解析(II)由PA,PB倾斜角互补知:kPA=-kPB,λ=kPA+kPB=0.由定理1得:当λ=0,则直线AB有定向,即,所以kAB是非零常数.

例3(2005年高考江西卷理科第20题)如图2,M是抛物线y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.

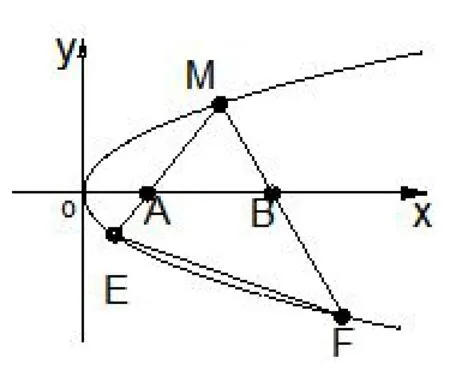
图2

(1)若M为定点,证明:直线EF的斜率为定值;(2)略.

解析(1)设定点M坐标为(x0,y0),由MA=MB知:kME+kMF=0.由定理1知,直线EF有定向,即(定值).所以直线EF的斜率为定值.

例4(2009年高考辽宁卷理科第22题)已知椭圆C过点,两个焦点为(-1,0),(1,0).

(1)求椭圆C的方程;

(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.

解析(I)由题意,c=1,可椭圆

(II)由题设知:λ=kAE+kAF=0.由定理1得:直线EF有定向,即

例5(2016年浙江(高中)竞赛第17题)已知椭圆方程,经过点,离心率为过椭圆C的右焦点作斜率为k的直线l,交椭圆于A,B两点,记PA,PB的斜率为k1,k2.

(I)求椭圆的标准方程;

(II)若k1+k2=0,求实数k的值.

解析(I)由已知:代入椭圆方程及,解得:a2=25,b2=16,即

(II)由定理1得:λ=k1+k2=0,则直线AB有定向,即.(注:题目中“过椭圆C的右焦点作斜率为k的直线l”的条件属于冗余条件,可去掉.文[13]化了很长篇幅讨论冗余条件问题,本文证明简捷明快).

3.求证(解)常数

例6(2017年全国(高中)数学联赛第11题)作斜率为的直线l与椭圆1交于A,B两点(如图3所示),且在直线l的左上方.

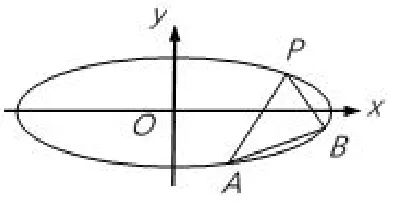
图3

(1)证明:△PAB的内切圆的圆心在一条定直线上;(2)略.

证明(1)由定理1逆命题知,直线AB斜率为,有定向,则故kPA+kPB=0.又P在直线l的左上方,因此,∠APB的角平分线是平行于y轴的直线,即△PAB的内切圆的圆心在直线上.

例7(2013年高考江西卷理科第20题)如图4,椭圆C:经过点,离心率,直线l的方程为x=4.

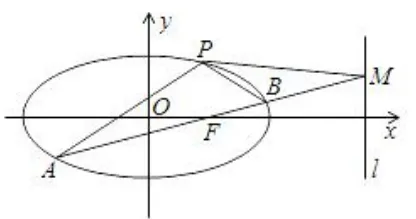
图4

(1)求椭圆C的方程;

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.

解析(1).(过程从略.)

四、通解的拓展

对于定理1、定理2,如果P(x0,y0)不在曲线上,仿文[14]证法,结合定理1、定理2的“平移法”构建齐二次方程,可猜想并拓展如下命题(限于篇幅证明过程略).

定理3已知常态二次圆锥曲线F(x,y)=Ax2+By2+Cx+Dy+E=0(A2+B2/=0),给定的一点P(x0,y0),过P作两条直线GH、IJ交曲线于G、H、I、J四点(记直线PGH、PIJ斜率分别为kPGH=k1,kPIJ=k2),M,N分别是弦GH,IJ的中点.记F1=2Ax0+C,F2=2By0+D,则有:

(1)若k1+k2=λ(λB/=0),直线MN恒过定点.

(2)若k1k2=λ(A-λB/=0),则直线MN恒过定点.

当P(x0,y0)在二次圆锥曲线上时,此时点P与G、I重合,则HJ一定过定点T(xT,yT),S为PT的中点.由中点坐标公式知:当k1+k2=λ(λB/=0),HJ恒过定点;若kk=λ(A-λB/=0),12HJ恒过定点.这与定理1、定理2的第(2)项结论是一致的.令P坐标为(m,n),曲线分别取y2=2px(p＞0),代入本文定理3,所得结论,正是文[14]中定理1、定理2、定理3结论.(摘编如下表3).

表3