2018年高考全国卷I理科第16题的解法分析及其题型归类

广东省湛江一中培才学校(524037) 魏 欣

在近几年各地高考中,三角函数最值问题屡屡受到命题者青睐.其出现的形式,或者是在小题中单纯地考察三角函数的值域问题;或者是隐含在解答题中,作为解答题所考查的知识点之一;或者在解决某一问题时,应用三角函数有界性会使问题更易于解决(比如参数方程).解决这一类问题的基本途径,一方面应充分利用三角函数自身的特殊性(如有界性等),另一方面还要注意将求解三角函数最值问题转化为求一些我们所熟知的函数(二次函数等)最值问题.本文就2018年高考全国I卷理科数学第16题,分析出三角函数最值的通法,归纳出三角函数最值的求解的主要五种模型,并举例历年高考题介绍求三角函数的最值.

一、题目展示与分析

题目(2018年全国I卷理科第16题)已知函数f(x)=2sinx+sin2x,则f(x)的最小值为____.

解析已知f(x)为奇函数,,T=2π,所以fmin(x)=-fmax(x).结合y=2sinx与y=sin2x图像特点知,当时,f(x)可取到最大值.

方法一(求导法)当时,f′(x)=2cosx+2cos2x=2(2cosx-1)(cosx+1).当时,f′(x)＞0,当时,f′(x)＜0.所以,因为fmin(x)=-fmax(x),所以.所以f(x)的最小值为.如图1所示.

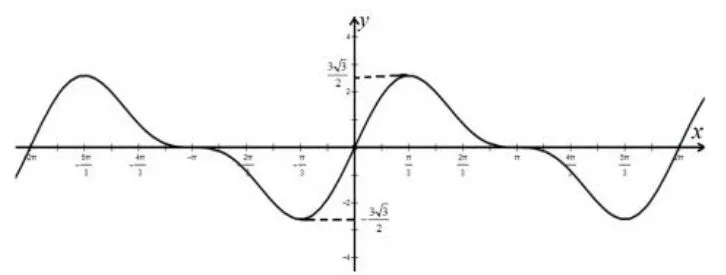
图1

评析用导数法求三角函数的最值是处理此类问题的通法,求导判断函数的单调性,考虑到最大值易于理解与求解,就先求出最大值,再结合函数图像的对称性求出最小值,或许这种方法是命题者的初衷.

方法二(均值不等式法)当时,

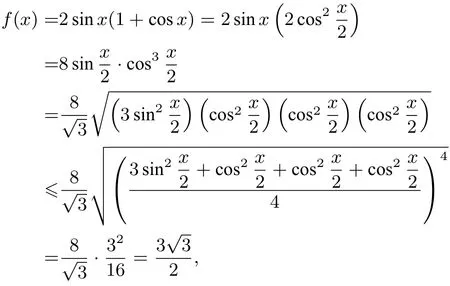
评析用均值不等式法求三角函数的最值,先做恒等变换,再适当配凑,然后利用四元均值不等式,算出最大值,再利用原函数图像的对称性转化为最小值,这种思路的难点在于积式的配凑,配凑的目的是用了均值不等式后要得到常数,再考虑等号成立是否有意义,尽管具有一定的技巧性,但也不失为一种好方法.

二、高考题型归类分析

在近几年各地高考中,三角函数最值问题屡屡受到命题者青睐.三角函数的最值问题是对三角函数基础知识的综合应用,一般题目给出的三角关系式往往比较复杂,必须进行化简后,再进行归纳.下面归纳出三角函数最值的求解的主要五种模型及其解题通法.

(一)一次函数型

三角函数的最值问题的一次函数型主要是指可以化为基本类型y=asinx+b或y=acosx+b的问题,主要有以下五种模型.

模型1y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B

例1(2014年高考北京卷第16题第2小问)求在区间上的最大值和最小值.

解析因为,所以.于是,当,即时,f(x)取得最大值0;当,即时,f(x)取得最小值-3.

模型2y=asinx+bcosx+c

对于y=asinx+bcosx+c型的函数,可通过辅助角公式,使函数转化为(其中,再利用有界性加以解决.

例2(2016年高考上海卷)若函数f(x)=4sinx+acosx的最大值为5,则常数a=___.

解析由φ)(其中)的最大值为5,得,解得a=±3.

模型3y=asin2x+bsinxcosx+ccos2x+d

这一模型的最值求法是通过降次转化为模型2,其中利用降幂公式.

例3(2015年高考浙江卷文科)函数f(x)=sin2x+sinxcosx+1的最小值是___.

解析f(x)=sin2x+sinxcosx+1=

模型4y=sin(mx+α)±sin(mx+β)或y=cos(mx+α)±cos(mx+β).

这一模型的三角函数,先用两角和与差的正余弦公式展开,整理后可以转化为模型2,化为一个角的三角函数形式后,再求最值.

例4(2013年高考安徽卷)设函数f(x)=sinx+.(1)求f(x)的最小值,并求使f(x)取最小值的x的集合;(2)略.

解析(1)即此时x的取值集合为.

模型5y=sin(mx+α)cos(mx+β)或y=sin(mx+α)sin(mx+β)

这一模型的三角函数,先用两角和与差的正余弦公式展开,再利用乘法运算展开,整理后可以转化为模型3,再化为一个角的三角函数形式后,最后求最值.

例5(2013年高考北京卷第2问)求f(x)=在区间上的最大值和最小值.

解析

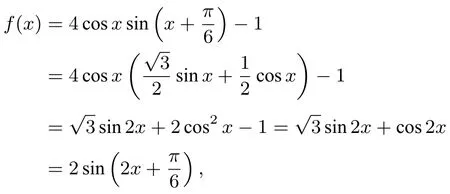
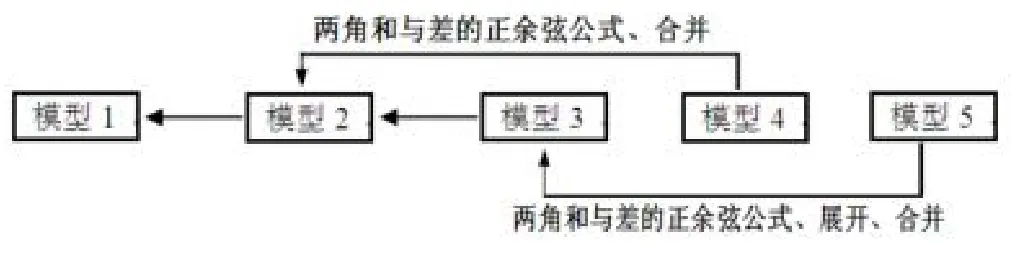
图2:模型1-5的转化关系

(二)二次函数型

模型6(同名)y=asin2x+bsinx+c或y=acos2x+bcosx+c

这里的同名是指二次项与一次项的三角函数名称相同,这一模型的最值的求法是直接转化为关于sinx或cosx的二次函数在区间上的最值问题.

例6(2016年高考全国卷II)函数f(x)=1-2sin2x+6sinx在上最大值和最小值之和为( )

解析,当sinx=1时,即时,fmax(x)=5,当,即时,.所以,故选C.

模型7(异名)y=asin2x+bcosx+c或y=acos2x+bsinx+c

这里的异名是指二次项与一次项的三角函数名称不同,即一个是正弦另一个是余弦,这一模式的最值的求法是用公式sin2x=1-cos2x或cos2x=1-sin2x将其转化为模型6.

例7(2011年高考北京卷理科)已知f(x)=2cos2x+sin2x-4cosx,求函数f(x)的最大值与最小值.

解析因为

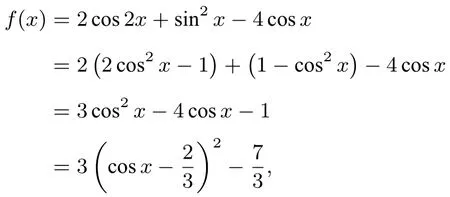
又因为cosx∈[-1,1],所以当时,;当cosx=-1时,f(x)max=f(-1)=6.

模型8(“正余弦三姊妹”聚会)y=f(sinx±cosx,sinxcosx)整式型

“正余弦三姊妹”聚会是指在所求函数中出现sinx±cosx,sinxcosx三者中的两个或三个.这一模型的最值的求法是通过把三角函数化为代数函数求最值.

例8(2015年高考安徽卷文科16(2))已知函数f(x)=sinx+cosx+sinx·cosx.求f(x)在区间上的最大值和最小值.

解析令t=sinx+cosx,则,当以当所以当.

评注在换元时,通常令t=sinx+cosx,则sinx·cosx=.

(三)分式函数模型

模型9

例9(2015年高考重庆卷改编)求函数f(x)=的最值.

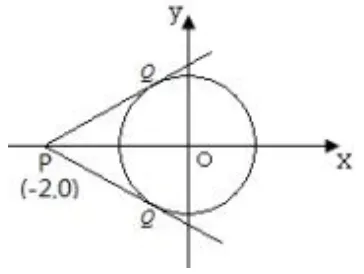
图3

解析,其几何意义是过定点P(-2,0)和单位圆上的动点Q(cosx,sinx)的直线的斜率,于是把求函数的最值问题转化为求该直线斜率的最值问题.如图,利用数形结合法,可知直线y=k(x+2)与单位圆x2+y2=1相_切时取得该直线斜率的最值.由,所以

(四)高次幂函数模型

对于y=asinnx+bcosmx型的函数,往往也可以利用导数法来求最值.

例10(2008年高考安徽春季卷)函数f(x)=sin4x+cos2x的最大值为___.

解析对函数求导,f′(x)=4sin3x·cosx-2cosx·sinx,令f′(x)=0,即4sin3x·cosx-2cosx·sinx=0,解得sinx=0或cosx=0或.当sinx=0或cosx=0时,f(x)=1,当时,.因此函数f(x)=sin4x+cos2x的最大值为1.

(五)对勾函数模型

例11(2012年高考上海春季卷)已知x∈(0,π),则函数的最小值为____.

解析此题为型三角函数求最值问题.因为x∈(0,π),所以sinx＞0,当a＞0时,不能用基本不等式来求最值,可以利用对勾函数的单调性来求最值.设在(0,1]上为减函数,故当t=1时,.所以函数的最小值为3.

用导数解三角问题的基本思路是“构”、“导”、“令”、“得”:一、构造函数;二、求导;三、设导数函数等于零或大于零或小于零;四、根据题意得出要求的结论.解题的关键是“得”,即如何运用导数可以判断单调性和求极大或极小值的性质得到要求的结论.利用导数解三角往往可以避免用三角公式进行繁琐的三角变换从而减少计算量,不但过程简单,而且方法新颖别致.通过练习可以增强知识之间的融会贯通,拓展知识面,对提高解题能力和培养创新意识具有重要意义.

求三角函数最值问题,综合性强,解题方法灵活多样,而且有的问题本身解法并不是各自独立的,而是相互依存,又相互联系;我们通过以上各种解题方法的探究,使我们对数学动态美和辩证的关系有了进一步的系统认识,对解这方面的题目能起到事半功倍的作用.