椭圆的极点极线性质及推论
北京化工大学附属中学(100029) 韩 毅
北京市朝阳区教育研究中心(100028) 蒋晓东
1.研究的缘起
在高考解析几何题当中,经常会遇到求定值、定点、以及共线等等问题.这些问题的背后隐藏着更深层次的理论—极点极线理论.极点极线是法国数学家笛莎格于1639年在射影几何学奠基之作《圆锥曲线论稿》中提出的.
初次接触极点极线理论是在王雅琪所写的《高观点下的北京高考解析几何试题》一文中,此文介绍了极点极线的定义、两个推论和以极点极线为背景的高考解析几何试题[1].该文并没有对相关推论进行证明.查阅资料发现范方兵、王芝平所写的文章《代数几何相转化相映成辉是一家》中,借助2018年北京高考的抛物线解答题,探究了该题的命题理论背景—极点极线理论,并介绍了调和点列及调和线束等概念[2].张留杰的《基于抛物线的一条性质的类比推广》一文中,借助极点极线理论使得2017年北京高考理科的抛物线解答题结论得以推广到一般的二次曲线[3].从以上文章中不难看出,以极点极线理论为背景命制的高考试题比较常见,但是极点极线在椭圆中如何体现的呢?它们的性质有哪些?推论有哪些?它们的推论以及性质是如何得到的呢?这些性质以及推论如何体现在高考试题当中呢?这些细致的问题值得研究与探讨.
2.椭圆的切线以及切点弦直线
首先,如果点P(x0,y0)在圆O:x2+y2=1上,则过点P(x0,y0)与圆O相切的直线为x0·x+y0·y=1.那么,当点P(x0,y0)在椭圆上,用隐函数求导法、判别式法或仿射变换法,易求得过P(x0,y0)的切线为;用仿射变换法求该切线方法如下:
证明设则椭圆C变换为x′2+y′2=1,P(x0,y0)变换为,即.过点与圆x′2+y′2=1相切的直线为1,即.
若点P(x0,y0)在椭圆C:外,如图1,则过P可以作椭圆C的两条切线,切点为F,G,那么直线是过两个切点F,G的直线,俗称切点弦直线.证明如下:

图1
证明设F(x1,y1),G(x2,y2)在椭圆上,因为PF,PG为椭圆的两条切线,所以直线PF,PG方程分别为,又因为点P(x0,y0)在直线PF,PG上,所以进而可知点F(x,y),G(x,y)1122在直线,所以直线为过两个切点F,G的直线方程.
若点P(x0,y0)在椭圆内部,但非中心(0,0)时,依然可以得到一条的直线.那么这条直线与椭圆的位置关系是什么呢?分两种情况讨论一下:
①若y0=0,带入可得:x=.当|x0|<a,P在椭圆内,由于,直线与椭圆相离;当|x0|=a,P在椭圆上,由于,直线与椭圆相切;当|x0|>a,P在椭圆外,由于,直线与椭圆相交.
②若y0/=0,联立直线与椭圆方程:利用判别式Δ=;当P在椭圆内,由于0,Δ<0,直线与椭圆相离;当P在椭圆上,由于,Δ=0,直线与椭圆相切于P;当P在椭圆外,由于直线与椭圆相交.
上述讨论可以得到,①当点P(x0,y0)在椭圆C:上,直线为过点P(x,y)00的切线;②当点P(x0,y0)在椭圆外,那么直线是过两个切点的直线,即切点弦直线.③当点P(x0,y0)在椭圆内,那么直线在椭圆外.
3.椭圆极点与极线
3.1 极点极线的定义
事实上,点P(x0,y0)(不是原点)与直线,就是相对于椭圆的一对极点与极线.对于圆锥曲线的极点极线,有统一的定义:
已知圆锥曲线Γ:Ax2+By2+2Cx+2Dy+E=0,则称点P(x0,y0)和直线l:Ax0x+By0y+C(x+x0)+D(y+y0)+E=0是圆锥曲线Γ的一对极点和极线[4].
3.2 椭圆的极点与极线的性质
在平面直角坐标系xOy中,极点P(x0,y0)(不是原点)相对于椭圆的极线为;有如下性质:
①一个确定的极点,有唯一确定的一条极线;反之亦然.
②如图2,若极点P(x0,y0)在椭圆内,极线与椭圆相离,该极线是椭圆中过P点的割线的两端点处切线的交点轨迹.
如图3,若极点P(x0,y0)在椭圆上,极线与椭圆相切于极点P.
如图4,若极点P(x0,y0)在椭圆外,极线与椭圆相交且为椭圆的切点弦直线(已证).
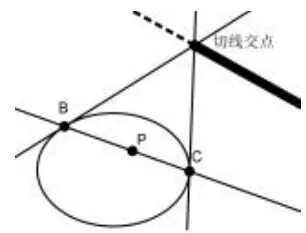
图2

图3

图4
③当极点P(0,m)在y轴上时,极线为平行于x轴;当极点P(n,0)在x轴上时,极线为平行于y轴;特别的当极点P(±c,0)为椭圆的焦点时,极线为平行于y轴且为椭圆的准线.
④设极点P(x0,y0)不在坐标轴上,则直线OP的斜率为kOP,极线,其斜率为k,则.特别的,当极点P(x,y)00在椭圆内,用点差法易证明极线f平行于以P为中点的弦所在直线EF.直线OP与椭圆相交于点D,过点D作椭圆的切线i,则以P为中点的弦所在直线EF、过点D的切线i,极点P的极线f,三线相互平行,如图5.

图5
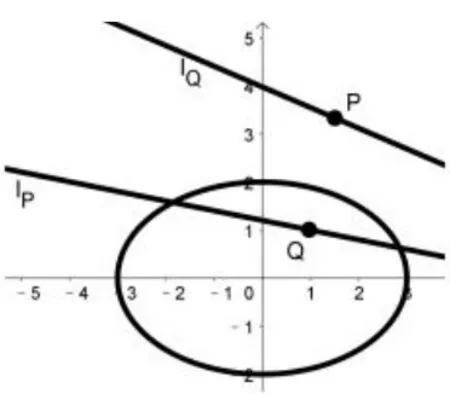
图6
⑤设点P的极线为lP,点Q的极线为lQ,如图所示,若lQ过点P,则lP过点Q,如图6.证明如下:
设点P(xP,yP),则相应的极线为1,点Q(xQ,yQ),相应的极线为.因为lQ过点P,则P点坐标满足方程,那么;即点Q坐标满足方程,也就是l过点Q.P
由此可得结论,如图7,共线点的极线必然共点(A、G、D、E四点共线,它们的极线a、g、d、e共交点F);共点线的极点必然共线(直线a、g、d、e共交点F,它们的极点A、G、D、E四点共线).

图7

图8
3.3 椭圆的极点与极线的推论
推论1如图8,射线OP与椭圆交于点D,与点P的极线交于点C,则|OP|·|OC|=|OD|2;当点P在x轴上时,|OP|·|OC|=a2;当点P在y轴上时,|OP|·|OC|=b2.
证明设点P(x0,y0),则其极线为1,当点P不在x轴上时,直线OP的方程为.联立方程组:解得.联立方程组:解得,所以

易知当点P在x轴上时,|OP|·|OC|=a2;当点P在y轴上时,|OP|·|OC|=b2.

图9

图10
证明如图10,过点P(x0,y0)(不在椭圆上)作椭圆的两条割线,分别交椭圆于A、B、C、D四点,设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).因为,所以(x1-x0,y1-y0)=λ(x2-x0,y2-y0),即
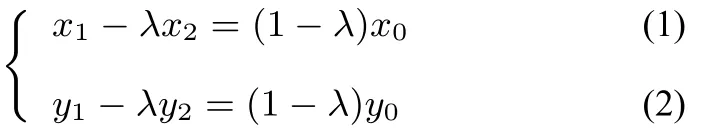
又因为A、B在椭圆上,即有

由(3)-(4)×λ2得:;整理得:

将(1),(2)代入(5)b2(x1+λx2)(1-λ)x0+a2(y1+λy2)(1-λ)y0=a2b2(1+λ)(1-λ);即:;两边同除以a2b2(1+λ)得:1.设点,从上式可以看出点恰好在直线上.又因为A(x1,y1),B(x2,y2),所以点为的定比分点,即.所以有,且点M恰好在点P关于椭圆的极线上.同理,在线段CD上可以找到一个点N,使得,且点N恰好在点P关于椭圆的极线上.所以且(内分比=外分比),则直线MN就是极点P(x0,y0)关于椭圆的极线.
如图11,不仅点M、N在极点P(x0,y0)的极线上,直线AD、BC的交点Q,以及直线AC、BD的交点R,也都在该极线上.证明这个需要了解两个著名的定理:梅涅劳斯定理以及塞瓦定理.

图11
梅捏劳斯定理如图12,13,若一条不过A、B、C三点的直线与△ABC的边AB、BC、AC所在直线分别交于D、E、F,则.

图12

图13
塞瓦定理如图14,15,已知平面上△ABC和点D(点D不在△ABC的三边上),直线AD,BD,CD分别交直线BC、CA、AB于F、G、E,则.

图14
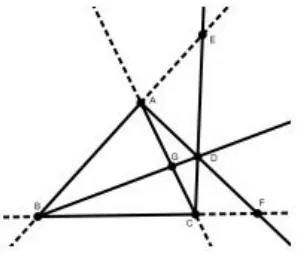
图15
推论2如图16,在完全四边形ABCD中,DB与CA的的延长线相交于R,BA与DC的的延长线相交于P,直线AD与BC相交于Q,若且(内分比=外分比),则点M、N在直线QR上.

图16

图17
证明先证明点N在直线QR上,如图17,连接QR交PD于点N′,在△RCD中,因为RN′,CB,DA共点Q,由塞瓦定理得:;又因为P,A,B共线,由梅涅劳斯定理得:;比较以上两式即有.又因为,所以,即点N,N′重合.
再证明点M在直线QR上,如图18:连接QR交线段AB于点M′,在△AQB中,因为QR,AR,BR共点R,由塞瓦定理得:;因为P,C,D共线,由梅涅劳斯定理得:;比较以上两式即有.又因为,所以,即点M,M′重合.综上所述:M、N点在直线QR上.
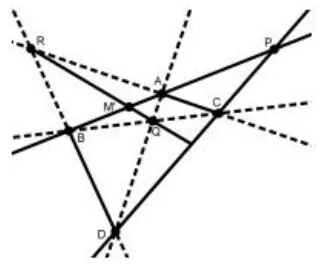
图18
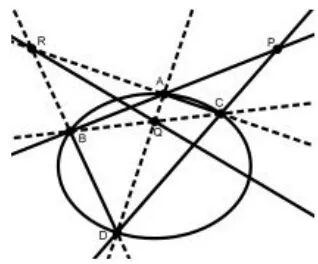
图19
推论2的意义在于给出了画极点P所对应的极线的快速方法.如图19,过点P(x0,y0)(不在椭圆上)作椭圆的两条割线,分别交椭圆于A、B、C、D四点,在完全四边形ABCD中,直线AD、BC相交点Q,以及直线AC、BD相交点R,则直线QR即为点P(x0,y0)的极线.
推论3如图20,若P、A、M、B为一组调和点列(即满足,则.
证明若,则
推论4设完全四边形ABCD为椭圆的内接四边形,且则点P的极线为RQ;点Q的极线为RP;点R的极线为PQ,称△PQR为自极三角形,如图21.

图20

图21
推论5如图22,设四边形ABCD为椭圆的内接梯形,AC//BD,AD∩BC=Q,则点P的极线过Q,且与直线AC、BD平行.特别的如图23,若BC//AD//y轴时,点P的极线平行y轴,且与x轴的交点R也是AC、BD交点,根据推论1有|OR|·|OP|=|OF|2=a2.
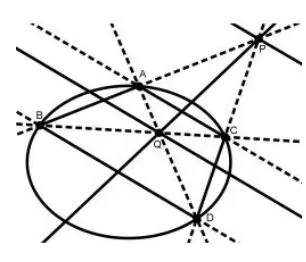
图22
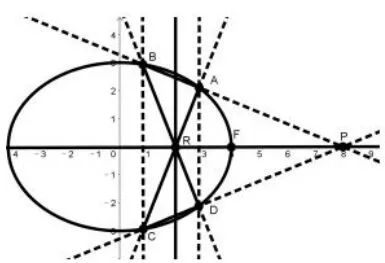
图23
4.极点极线理论在高考试题中的体现
例题1(2008年高考安徽卷理科)设椭圆1(a>b>0)过点,且着焦点为.
(I)求椭圆C的方程;(II)当过点P(4,1)的动直线l与椭圆C相交于两不同点A,B时,在线段AB上取点Q,满足,证明:点Q总在某定直线上.
背景分析(II)因为,所以PQ调和分割AB(即P、Q两点为线段AB的内外分点).所以点Q在点P的极线上,而点P的极线为2x+y-2=0,所以点Q总在2x+y-2=0上.
例题2(2010年高考江苏卷)在平面直角坐标系xOy中,如图24,已知椭圆的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.
(I)设动点P满足PF2-PB2=4,求点P的轨迹;
(III)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
背景分析(III)因为直线MN与直线AB的交点必在点T的极线上,而点T在直线x=9上.所以点T的极线必共点,且该点为直线x=9的极点,此点即为直线MN必过的定点.因为,直线x=9的极点为(1,0),所以,直线必过点为(1,0).

图24
例题3(2011年高考四川卷)如图25,椭圆有两顶点A(-1,0)、B(1,0),过其焦点F(0,1)的直线l与椭圆交于C、D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
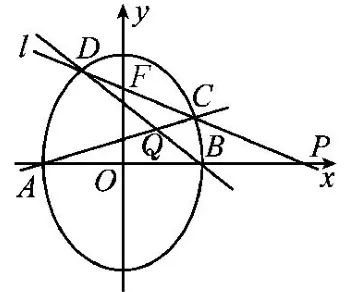
图25
(II)当点P异于A、B两点时,求证:为定值.
背景分析(II)设P(t,0),则点P的极线过Q.因为椭圆方程为,所以点P(t,0)的极线为,即.所以1.
例题4(2012年高考北京卷理科)已知曲线C:.
(I)若曲线C是焦点在x轴上的椭圆,求m的取值范围;
(II)设m=4,曲线C与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线C交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
背景分析(II)如图26,直线AN与BM的交点必在点P(0,4)的极线上,而点P(0,4)的极线为y=1.所以直线AN、直线BM、直线y=1共点,所以A,G,N三点共线.

图26
5.小结
许多高考解析几何试题的命制都是以极点极线理论作为指导的,因此对于极点极线理论的了解,有助于把握命题者的意图,明确解决问题的方向,优化运算.探究极点极线性质、推论有较高的教育教学价值,因此作为一线教师可以有所了解.

