等式中两个变量取值问题的解法探究

安徽省灵璧师范学校(234200)陈 伟

在基本不等式中,常常会涉及到两个变量等式,求这两个变量的积或线性和的取值范围问题.本文结合具体实例探究这类问题的基本解题思路.

例1已知x＞0,y＞0且,求x+y的取值范围.

解法1(常值代换)

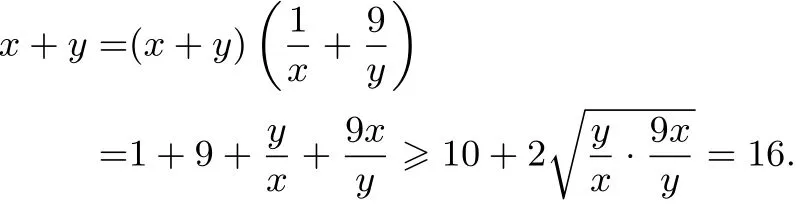
点评如果已知两个正数和为定值,求其倒数的线性和的取值范围问题,基本的解题思路是常值代换法,展开利用基本不等式求解.

解法2(化为一元函数)由x＞0,y＞0且知,

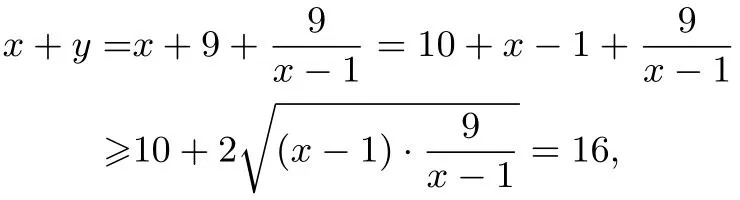
点评这种解法运用函数与方程思想,把二元问题转化为一元函数,可以用基本不等式,也可以用导数解决.

解法3(判别式)设x+y=t,y=t-x代入整理得x2+(t-8)x+t=0,关于x的一元二次方程有解,于是Δ=(t-8)2-4t=t2-20t+64=(t-4)(t-16)≥0,所以t≤4或t≥16,又由x＞1,y＞9知t≥16,所以x+y的取值范围是[16,+∞).

点评用到换元的思想方法,把问题转化成一元二次方程,用判别式来解决,最后还得结合条件进行取舍.这也是解决这类问题常用的方法.

解法4(配凑法)由知x＞1,y＞9,变形得x+y≥16,所以x+y的取值范围是[16,+∞).

点评这种解法需要对表达进行恰当变形,技巧性较强.

解法5(数形结合)

由x＞0,y＞0且知.平移直线x+y=0且与曲线y=9)相切时x+y取得最小值.令得x=4,求得y=12时,此时x+y取得最小值16,所以x+y的取值范围是[16,+∞).

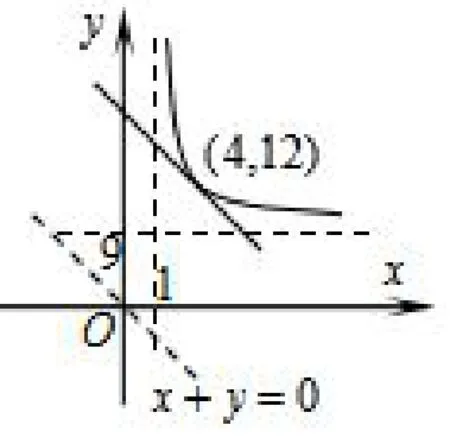
图1

点评转化成在约束条件下目标函数的取值范围问题,数形结合运用线性规划的基本思想方法.

解法6(向量法(柯西不等式))由于x＞0,y＞0,设向量,则.又由a·b=|a|·|b|cos〈a,b〉得1+3=,所以x+y≥16.当且仅当向量a与b同向,即x=4,y=12时,x+y取得最小值16,所以x+y的取值范围是[16,+∞).

点评这种解法是根据条件构造两个向量用数量积来求解,实际上是柯西不等式.

变形1已知x＞0,y＞0且.若a,b是正常数,求ax+by的取值范围.

解(常值代换).当且仅当,即时,ax+by取得最小值,所以ax+by的取值范围是.

变形2已知实数x,y,满足9x+y=xy,求x+y的取值范围.

解(判别式)设x+y=t,y=t-x代入9x+y=xy整理得x2+(t-8)x+t=0,关于x的一元二次方程有解,于是Δ=(t-8)2-4t=t2-20t+64=(t-4)(t-16)≥0,所以t≤4或t≥16,所以x+y的取值范围是(-∞,4]∪[16,+∞).

点评这个问题可理解为:在约束条件9x+y=xy下,求目标函数z=x+y的取值范围.结合图形,平移直线x+y=0且与曲线9x+y=xy相切时,即可得到x+y的取值范围.

图2

例2已知x＞0,y＞0且xy=x+y+1,求3x+2y的最小值.

解法1(化为一元函数)由x＞0,y＞0且xy=x+y+1知,

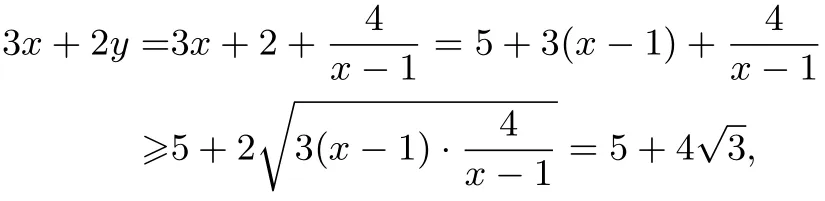
解法2(判别式)设3x+2y=t,代入xy=x+y+1整理得x2-(t+1)x+t+2=0,关于x的一元二次方程有解,于是Δ=(t+1)2-12(t+2)=t2-10t-23≥0,所以或,又由x＞1,y＞1知,当且仅当Δ=0,即,时,所以3x+2y取得最小值.

解法3(配凑法)由xy=x+y+1变形得(x-1)(y-1)=2且x＞1,y＞1,3x+2y=5+3(x-1)+2(y-1)≥5+,当且仅当3(x-1)=2(y-1),即时,3x+2y取得最小值.

注(1)本题可以求出3x+2y取值范围是[5+.(2)本题也可用线性规划的基本思想方法求解.

例3已知x＞0,y＞0且x+2y+xy=30,求xy的最大值.

解法1(基本不等式)由x+2y+xy=30得,得,即0＜xy≤18,当且仅当x=2y,即x=6,y=3时,xy取得最大值18.

解法2(化为一元函数)由x＞0,y＞0且x+2y+xy=30知,当且仅当,即x=6,y=3时,xy取得最大值18.

解法3(判别式)设xy=t,,代入x+2y+xy=30整理得x2+(t-30)x+2t=0,关于x的一元二次方程有解,于是Δ=(t-30)2-8t=t2-68t+900=(t-18)(t-50)≥0,所以t≤18或t≥50,又由0＜x＜30,0＜y＜15知t≤18,当且仅当Δ=0,即x=6,y=3时,xy取得最大值18.

注本题可以求出xy的取值范围是(0,18].

在解题过程中,尝试不同的视角分析解决同一个问题,可以强化知识间的联系,提高学生运用知识分析问题和解决问题的能力.