让必要性探路“探”得更明白些

广东省广州大学附属中学(510000) 韩智明

我们通常在进行一个数学问题转化的时候必须要特别注意问题的等价性,也就是需要同时考虑命题成立的充分性和必要性.但在很多时候,为了寻找解题突破口(尤其是突然有个猜想)时,往往需要先利用必要条件(或充分条件)探路,然后随后验证其充分性(或必要性),这就是必要性探路解题的思想方法.这种方法一般用于证明不等式恒成立问题.大量的教辅资料及杂志涉及到必要性探路的题常常会引起一些读者的质疑,质疑地是探路时取定义域里面的哪个数?为什么取那个数?怎样操作?几乎没有一本数学资料说清楚,因此此种解决数学问题的方法一直不被广大师生所接受和通用,也可能因为这与我们通常的解题思维区别较大,在找点的问题上缘由没有弄清楚.但在必要性探路解题活动中,由必要条件得到的范围是必须满足的范围,所以只需要限定在这个范围内进行就可以,而如果同时又证明了这个范围内所有数都可以取到,那么这个过程在逻辑上就是严密的,也不失为一种巧妙的处理数学问题的好方法.然而在证明必要性时究竟取什么值?怎样取值?一直是一个悬而未决的问题,下面就让我们一起去探个明白.

笔者在一次高三综合测试中遇到一道这样的导数压轴题:

试题已知函数f(x)=axex-(a+1)(2x-1).

(1)若a=1,求函数f(x)的图像在点(0,f(0))处的切线方程.

(2)当x＞0时,函数f(x)≥0恒成立,求实数a的取值范围.

大家看到这道题,当然会想到很多方法,至少不少于四种通解通法,然而此题的参考答案是这样给的:

解析(1)略.(2)因为当x＞0时,函数f(x)≥0恒成立,所以f(1)≥0,所以.

解法1由题意,得f′(x)=a(x+1)ex-2(a+1).令f′(x)=h(x),则h′(x)=a(x+2)ex在x＞0时恒为正数,所以函数h(x)即f′(x)在(0,+∞)上单调递增.而f′(0)=-2-a＜0,f′(1)=2ea-2a-2 ≥0,所以f′(x)存在唯一根x0∈(0,1],且函数f(x)在(0,x0)上单调递减,在(x0+∞)上单调递增,所以函数f(x)的极小值也是最小值为f(x0)=ax0ex0-(a+1)(2x0-1),故只需f(x0)≥0即可.由f′(x0)=0得a(x0+1)ex0-2(a+1)=0,即,代入上式可得,因为x0∈(0,1],所以,所以f(x0)≥0恒成立,所以.

当老师们看到这种解法后,感到方法巧妙地同时又有点蒙的感觉,学生看到后更是百思不得其解,共同的疑惑是为什么要取值1,而不是其它的数,而且代入1正好是参数的取值范围,这就是证明不等式恒成立时所运用的一种证明方法,即必要性探路法.纵观各种教辅资料关于运用必要性探路法证明不等式恒成立问题的时候,从来都没有把证明过程说清楚,代什么数?为什么代某个数正好得到参数范围?都是给出答案的人在幕后操作,很少走向前台,有些老师少于研究不知个中缘由,更不要说接受教育的学生了.于是见到这种方法解题,多数老师直接避开或寻找其它的解题方法了,甚至教育学生不要用这种不好解释的方法解题,放任学生的一片迷茫.我当然也是一样的心理,但作为传道、授业的老师,解惑是我们的职业,面对学生们的疑惑,我们责无旁贷地要弄清楚、想明白这种解题方法的来龙去脉,同时对老师自己的专业水平也是一个很大的提升.

思路探求题目答案中先取特殊值1的依据是什么?由当x＞0时,函数f(x)≥0恒成立,x取2时得到f(2)≥0,即为什么不是这个结果呢?这时有人会说x取2时得到a的取值范围在证其充分性的时候不成立,这样一说仿佛有道理,试问我们是不是要把题目定义域范围内的数取遍然后逐一验证呢?这样的话不现实,关键还是要回到为什么x取1的问题上来.

首先我们观察所证不等式的特征,由f(x)=axex-(a+1)(2x-1)≥0在(0,+∞)上恒成立转化为axex-2(a+1)x+a+1≥0在(0,+∞)恒成立.即axex≥2(a+1)x-a-1,我们先可以假设g(x)=axex以直线h(x)=2(a+1)x-a-1为切线,设切线的切点为P(x0,y0),则由g′(x)=a(x+1)ex,h′(x)=2(a+1),得到解得

这时我们画出两函数图像如图1可知,当取1时显然是两条曲线的临界值,如果x取其它值就会把条件加强,其得到的的取值范围则是当a取1时得到a的取值范围的子集,故在本题中x应该取1,只是出题人隐去了这一思维步骤,结合图像和解答我们就明白为什么x取1,而不是其它数了.

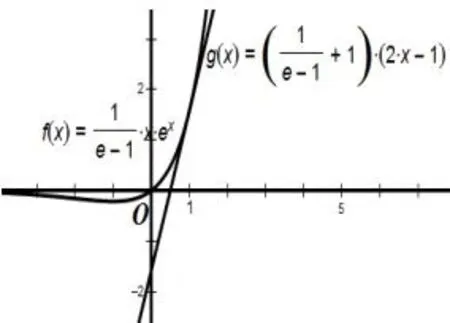
图1

其实根据这种解法,先用必要性探路找a的取值范围时,做题之前是要做很多功夫作铺垫的,当确定a的范围后,第二步就只要证明其充分性满足就可以了,其本质是切线放缩和寻找切点的问题,下面给出证明充分性的第二种证法.

解法2由f(x)=axex-(a+1)(2x-1)得f(x)=a(xex-2x+1)-2x+1.令M(x)=xex-2x+1,则M′(x)=(x+1)ex-2在(0,+∞)上单调递增.因为M′(0)=1-2=-1＜0,M′(1)=2e-2＞0,据零点存在定理可知,∃x0∈(0,1)使得M′(x0)=0,即,易知M(x)min=,因为x0∈(0,1),所以M(x0)＞0,即M(x)=xex-2x+1＞0.所以f(x)=a(xex-2x+1)-.令N(x)=xex-2ex+e,因为N′(x)=(x+1)ex-2在(0,+∞)上单调递增,由N′(1)=0易知N(x)min=N(1)=0,所以f(x)≥0.

方法点睛通过上面的剖析,我们知道必要性探路所取的值并不是随意的,而是有“预谋”的,是经过对不等式的等价转化分析,寻找切点,确定临界值然后利用切线放缩证明其充分性成立,只是在一些运用此法解题过程中没有分析怎样取值的问题.

现在我们不妨通过这种思想方法去尝试解几道题.

题2已知函数.

(1)若对任意的实数a,函数f(x)和g(x)的图像在x=x0处的切线总相等,求x0的值.

(2)若对∀x＞0,不等式f(x)-g(x)≥1恒成立,求正实数a的取值范围.

思路探求第(1)问显然是第(2)问的铺垫,通过第(1)问找出切线和切点,为第(2)问利用必要性探路法解题时直接可以得到取x=1.

解析(1)因为f(x)=ax+,所以由题设知x0＞0且f′(x0)=g′(x0),即,所以,即,因为对任意实数a恒成立,所以解得x0=1,故x0=1.画出两个函数图像如图2知,x=1是所取的临界值.

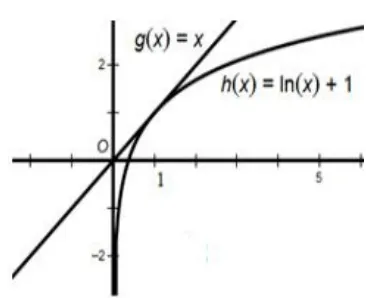
图2

(2)令h(x)=f(x)-g(x)-1(x＞0),只需证明h(x)≥0即可.由h(1)=f(1)-g(1)-1≥0得a≥1.下面证明当a≥1时,h(x)≥0成立即可.因为,令M(x)=x-lnx-1,则,易知M(x)在(0,1)递减,在(1,+∞)递增.所以M(x)≥M(1)=0,所以h(x)≥M(x)≥0,即f(x)-g(x)≥1.综上,实数a的取值范围是[1,+∞).

方法点睛利用第(1)问找到的临界值x=1代入原不等式得到参数a的取值范围,然后证明不等式成立的充分性,整个解题利用放缩等处理方法显得思路清晰,过程简洁.

题3已知函数f(x)=lnx-x2+ax,f(x)≤0恒成立,求实数a的取值范围.

思路探求此题属于恒成立问题,可以用必要性探路法处理,然而究竟首先取什么数呢?我们不妨对函数本身进行处理,由f(x)=lnx-x2+ax=0得到lnx=x2-ax,令g(x)=lnx,h(x)=x2-ax,设两个函数在x=x0处有公切线,求出此公切线的方程,此时取x=x0进行必要性探路,求出的a值就是临界值,就可以得到a的取值范围,然后再证明其充分性.

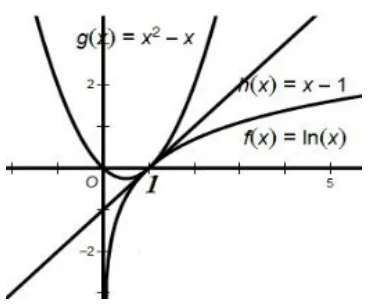
图3

解析设函数g(x)=lnx和h(x)=x2-ax的公切点为(x0,y0),则有,消a得,令φ(x)=lnx+x2-1(x＞0)可知其单调递增,又因为φ(1)=0,故x0=1,a=1.画出两个函数图像如图3知x=1是所取的临界值.取x=1即f(1)≤0得到a≤1.下面证明当a≤1时不等式恒成立.由f(x)=lnx-x2+ax≤lnx-x2+x,易证当x＞0时,lnx≤x-1,所以f(x)≤lnx-x2+x≤x-1-x2+x=-(x-1)2≤0,即证充分性成立,所以a≤1,即实数a的取值范围为a≤1.

方法点睛此题不同于题2,前者有第(1)问做铺垫,怎样取值和取什么值在第(1)问中通过求两条曲线的切线和切点即可得到,先把不等式分成两个函数,先令它们有公切线和公切点,求出其公切点即为运用此方法解题所要取的x值,求出参数a的范围,再代入原不等式证明其充分性成立,证明过程中运用到了放缩法和形如lnx≤x-1经典的不等式,整个解题步骤也是显得干净、利落.

题4已知函数

(2)f(x)≥g(x)在x＞0时恒成立,求实数a的取值范围.

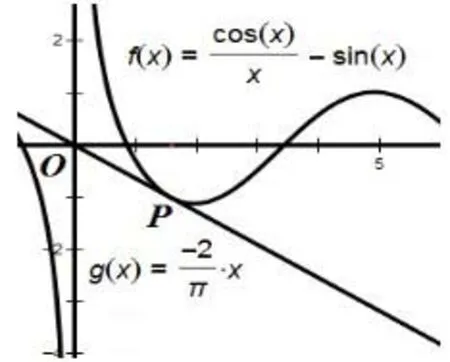
图4

思路探求第(1)问略:第(2)问如果用参变分离法或整体构造函数处理的话,难度很大,加上含有三角函数,求导非常复杂,如果用必要性探路法处理先要合理构造两个函数,通过观察所证不等式可以转化为证对∀x＞0恒成立的问题,为方便计算切线方程和切点坐标,可以化为证明成立.下面先令和 τ(x)=-ax相切,则设切点坐标为P(x0,y0),则有画出两个函数图像如图4可知,是所取的临界值.由下面证明充分性成立,当时,只要证明µ(x)=因为又因为所以当时,µ′(x)＜ 0,µ(x)单调递减,当时,µ′(x)＞ 0,µ(x)单调递增.所以即µ(x)≥0,即证所以即实数a的取值范围为

方法点睛处理恒成立问题的方法较多,有些利用分参后求导难得较大,操作性不强,此题运用必要性探路法处理,解题思路清晰,逻辑性强,是一种简化思维程序的好方法.教师在进行解题活动时,不仅要教给学生某种解题方法,更要教会学生学会恰当地选择某种方法,从而习得某种解题策略,这对学生的数学核心素养有很大的提升.为找临界值,合理地重新构造函数,求出两个函数的公切线和公切点,通过必要性探路得到参数的范围,然后利用放缩或者求导证明不等式成立的充分性.整个思维流程脉络明晰,一气呵成,由此可见必要性探路是处理此题最佳的策略和方法.

通过以上几个习题的解题分析,必要性探路法在解决恒成立问题中应该是一种不可或缺的解题策略,我们也更加清晰和明白它的应用范围和证明原理.我们在进行数学教学活动特别是数学解题教学活动时,不是一成不变的解题套路,当套路被“套”的时候,我们要灵活地去选择其它方法,其中一个首要任务就是教会学生怎样思考问题,怎样审题、怎样寻找解题的突破口以及灵活变通.当学生遇到一个陌生的数学问题或是看到某个难题的奇妙的解法弄不懂时,作为教学的组织者,我们除了传道、授业以外,解惑也是一个非常重要的环节.在高三后期的复习备考中,训练的综合性让试题的难度和深度都有加大,特别是一些压轴题的解题思路不容易发现甚至给学生不好讲解,有些试题的解决处理方法多种多样,当遇到这种情况的时候,某些教师严格遵循复习资料的参考答案,拘泥于参考答案的方法,让学生限于机械被动的接受学习中,缺乏解题前的准备,双方的互动和活动铺垫不够,对学生的能力和知识储备不了解,也就是说没有认清学生已经具备的认知结构,这样就根本就不能达到训练学生解题思维的效果,结果是当学生在每次遇到这种问题时仍然是一筹莫展.

“帮助学生学会数学地思维”是我们进行数学活动的核心所在,即在数学问题的解决过程中帮助学生理解数学问题的本质,要让学生学会用数学的思维思考问题,今天我们把必要性探路法“探”了个明白,然而在漫长的解题活动中,还有很多问题和陌生的领域需要我们去探着走,只有我们老师自己从观念上明白了所教授的数学问题的内容和本质,才能教给学生真正的数学,才能站在教学研究的制高点,准确把握数学学科的本质,才能知道学生什么时候需要和需要什么的问题,才能成为数学教育功能的执行者和传播者.