“气缸类型”在气体实验定律中的应用
李健华
(深圳市布吉高级中学 广东 深圳 518114)
气体实验定律的应用是热学的重点和难点,气体实验定律与牛顿定律、力的平衡问题有机地结合起来,形成综合性较强的力学问题,有利于考查综合分析能力及对物理过程的分析推理能力.在新高考要求中属于Ⅱ级要求,新课改以来作为选修3-3计算题部分,分值在10分左右,较好地考查了学生的核心素养.在2018年全国高考的7套物理试题中,其中涉及气体实验定律计算题部分的有全国Ⅰ,线框进入磁场的过程,安培力冲量Ⅱ,Ⅲ卷与海南卷共4套卷,并且其中就有3套试卷考查了“气缸模型类型”,可见研究好这一模型的规律,对今后的高考备考会有所裨益.
1 模型的特点
气缸类型的特点是通过活塞来将一定质量的理想气体封闭在缸内,主要有单缸单室类型、单缸双室类型和双缸双室类型等.这类问题中对力学压强求解是一个难点,对于力学研究对象一般取气缸、活塞或活塞上的物体,然后根据平衡状态或牛顿第二定律列方程求解.需要注意的是:首先,此类问题中压强的单位要用Pa便于计算,在实际教学中学生对面积单位的换算经常出错,要特别注意强调.其次,有两个或多个气缸时,要综合应用气体之间相互关联的问题,解题应分别研究各部分气体,找出它们各自的规律以及它们之间的相互联系来列方程.近几年高考中此类题出现概率较大,几乎年年有,如图1所示.
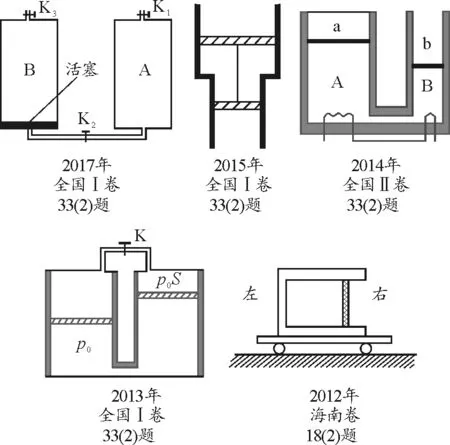
图1 近几年高中考中气缸气体考题
2 模型的应用
2.1 单缸单室
【例1】(2018年高考理综全国Ⅱ卷)如图2所示,一竖直放置的气缸上端开口,气缸壁内有卡口a和b,a,b间距为h,a距缸底的高度为H;活塞只能在a,b间移动,其下方密封有一定质量的理想气体.已知活塞质量为m,面积为S,厚度可忽略;活塞和气缸壁均绝热,不计它们之间的摩擦.开始时活塞处于静止状态,上、下方气体压强均为p0,温度均为T0.现用电热丝缓慢加热气缸中的气体,直至活塞刚好到达b处.求此时气缸内气体的温度以及在此过程中气体对外所做的功.重力加速度大小为g.
解析:由题意可知,对缸内气体进行加热后,气缸中的气体体积不变,发生等容变化,直至活塞开始运动.然后活塞缓慢上升,缸内气体的压强不变,发生等压变化直到刚好接触到b处.设活塞到达b处时缸内中气体的压强为p1,体积为V1,温度为T1,根据理想气体状态方程有
(1)
以活塞为研究对象,由力的平衡得
p1S=p0S+mg
(2)
由几何关系有
V0=SH
(3)
V1=S(H+h)
(4)
联立式(1)~(4)解得
(5)
而整个过程中气体对外所做的功为
W=(p0S+mg)h
(6)
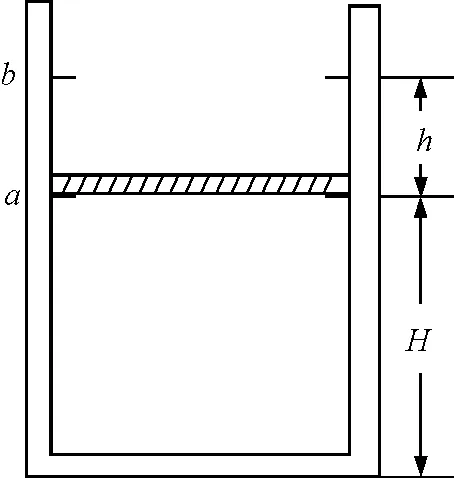
图2 例1题图
点评:本题气缸内只一个气室,属于“单缸单室”类型问题.解答本题的关键是要能够分析出不同的物理过程,实际过程中热学状态经过等容变化与等压变化.但此题只要抓住关键的初、末状态,不必理会变化时的中间过程,然后利用理想气体的状态方程来求解,简洁又能迅速求解,事半功倍.
2.2 单缸双室
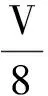
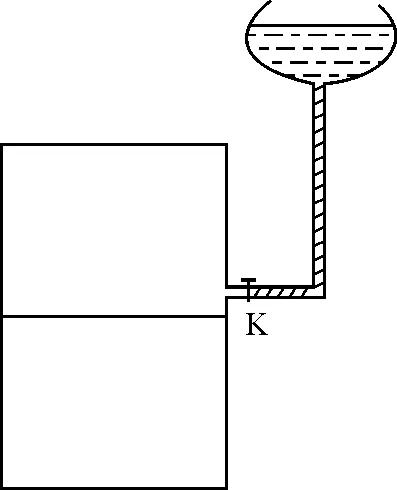
图3 例2题图
解析:以活塞上部分气体为研究对象,设其压强为p1,体积为V1;对活塞下部分气体,设其压强为p2,体积为V2.由于液体慢慢地流入气缸中,缸内气体上下两部分气体温度不变,由玻意耳定律得
(7)
(8)
根据题意由几何关系可知
(9)
(10)
若液体的质量设为m,根据力的平衡得
p2S=p1S+mg
(11)
联立解式(7)~(11)解得
(12)
点评:本题是属于典型的“单缸双室”类问题,气缸内分为上下两部分气体,解答此类问题的关键是:首先,明确研究对象,分别对上下两部分气体进行研究,找不同状态的状态参量.然后根据状态方程列方程求解.其次,根据缸内上下两部分气体的体积关系,以及对活塞进行力的平衡关系列出方程,然后进行求解.
【例3】(2018年高考海南卷)一储存氮气的容器被一绝热轻活塞分隔成两个气室A和B,活塞可无摩擦地滑动.开始时用销钉固定活塞,A中气体体积为2.5 ×10-4m3,温度为27 ℃,压强为6.0×104Pa;B中气体体积为4.0 ×10-4m3,温度为-17 ℃,压强为2.0 ×104Pa.现将A中气体的温度降至-17 ℃,然后拔掉销钉,并保持A,B中气体温度不变,求稳定后A和B中气体的压强.
解析:温度降低,然后拔掉销钉后,则活塞一定从压强大的一侧向压强小的一侧移动,直至A,B气缸里的压强相等,设A,B气缸中气体最终压强为p.
对A气室由状态方程
(13)
对B气室由状态方程
(14)
又由几何关系可得
(15)
联立式(13)~(15)解得稳定后A和B中气体的压强为
p=3.2×104Pa
(16)
点评:此题有两部分气体,属于“单缸双室”类型,解答本题的难点在于A中气体经过两个不同的物理过程,但只要抓住初、末状态,然后利用状态方程就能方便直接求解.另一难点是本题有两部分气体,所以对两部分气体要分别研究其各自的变化过程,关键是抓住它们之间的联系,即压强相等.还有就是体积的几何关系要把握好,弄清楚这些关系本题就能迎刃而解.
2.3 双缸双室
【例4】(2017年高考理综全国Ⅰ卷) 如图4所示,容积均为V的气缸A,B下端有细管(容积可忽略)连通,阀门K2位于细管的中部,A,B的顶部各有一阀门K1,K3,B中有一可自由滑动的活塞(质量、体积均可忽略).初始时,3个阀门均打开,活塞在B的底部;关闭K2,K3,通过K1给气缸充气,使A中气体的压强达到大气压p0的3倍后关闭K1.已知室温为27 ℃,气缸导热.
(1)打开K2,求稳定时活塞上方气体的体积和压强;
(2)接着打开K3,求稳定时活塞的位置;
(3)再缓慢加热气缸内气体使其温度升高20 ℃,求此时活塞下方气体的压强.
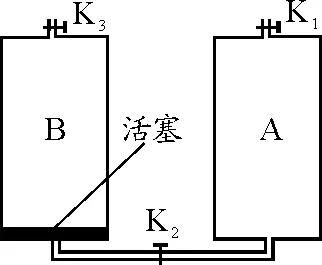
图4 例4题图
解析:(1)K2打开后,由于A中气体压强大于B中气体压强,则活塞一定上升,稳定时A,B中气体压强相等,设此时的压强为p1,B中气体的体积为V1,由玻意耳定律得
对A中气体有
3p0V=p1(2V-V1)
(17)
对B中气体有
p0V=p1V1
(18)
解得
(19)
(2)K3打开,则B与外界大气相连,故其压强为p0,而A中气体的压强为2p0,则活塞一定上升.若B气缸体积足够大,则A中气体的最终压强为p0,设此时A中气体的体积为V2,对一定质量的A中气体由玻意定律有
3p0V=p0V2
(20)
解得
V2=3V
(21)
而此时V2>2V,可见稳定时活塞最多上升到B的顶部位置.
(3)对A中气体分析可知,在升高温度时活塞静止不动,压强增大,设最终压强为p2,则A中气体压强由3p0到p2过程中,根据气体状态方程得
(22)
将数据T0=300 K,T1=320 K代入式(22)解得
p2=1.6p0
(23)
点评:该题有两个气缸,每个气缸只有一个气室,属于典型的“双缸双室”类型.由于此类型有两个缸两部分气体,因此变化过程复杂,需要用力学的观点来准确无误地分析各处压强之间的相互关系.在分析过程中,特别要清楚在研究相应的变化过程中,哪些量是不变的,哪些量是变化的,以及它们之间的相互关系.然后选择相应的气体实验定律进行求解,本题第3问选A中气体整个变化过程来研究,应用理想气体状态方程进行求解简洁快速.
3 结束语
围绕“气缸类型”设置的气体实验定律试题,由于这类问题涉及到力的平衡、牛顿第二定律和热学等相关的知识,这就要求学生具有良好的综合分析和思维能力,以及灵活运用知识解决问题的能力.因此,在考试复习时,如果学生能够全面地理解本文所总结的问题类型,掌握解决问题的方法,就能提高自己解决问题和分析问题的能力.当他们在高考中遇到类似这种类型的问题时,能够达到“手中有粮,心中不慌”的目标.

