斐波那契数的标准分解式中因子23的指数

严婉琳，钟球盛

（1.惠州城市职业学院 国际学院，广东 惠州 516000；2.广州番禺职业技术学院 机电工程学院，广东 广州 511483）

1 引言及预备知识

由数学家Leonardo Fibonacci提出的斐波那契数列，在化学、物理、数学、环境自然等多个领域有许多重要应用.斐波那契数列的第零项为0.第一项是1，此后，每项都为前两项之和.

定义1[1-2]斐波那契数列是指递推关系Fn=Fn-1+Fn-2(n≥2)所确定的数列{Fn}n≥0，这里的初始条件是F0=0,F1=1，并且Fn称为斐波那契数.

文献[3-10]分别研究了关于斐波那契数的标准分解式中因子2，3，5，7，11，13，17，19的指数.文献[11-12]则证明了斐波那契数的整除性.文献[13]不但提出了关于一般奇素因子p在Fd(p)标准分解式中指数的猜想，还探讨了对一般奇素因子p与d(p)=min{w：p/Fw}的整除关系.基于上述相关文献，本文研究得出斐波那契数Fn下标n的分解式中因数23的指数与24的指数将共同决定Fn标准分解式中因子23指数的结论.

引理1[6]4设m,n均是正整数，a整除b用“a|b”表示.若m|n，则有Fm|Fn成立.

引理2[6]5设m,n均是正整数，则Fm+n=FmFn-1+Fm+1Fn成立.

引理3设n是正整数，23|Fn⇔24|n.

逐一计算Fn(0≤n≤47)关于模23的最小非负剩余，设Fn≡m(mod23)，则可得表1.

表1 Fn关于模23的最小非负剩余

由此可得Fn关于模23的最小非负剩余的周期是48.Fn≡0(mod23)当且仅当n≡0(mod24).

引理4设m是一个正整数，则有F24m+1≡F24m-1(mod23)成立.

证明由引理3及斐波那契数的定义与性质可知，F24m≡F24m+1-F24m-1≡0(mod23)成立，故引理4成立.

引理5[9]214设m,p均是正整数，则有

引理6[9]215假设m是一个正整数，则有成立.

假设a,b均是整数，t是一个非负整数，记号at||b表示at|b且b不能被at+1整除.

2 相关证明

定理1设p,k均为正整数，则标准分解式中因子23的指数与标准分解式中因子23的指数相同.

证明引理3得设n=24kp且p为正整数.标准分解式中因子23的指数大于0恒成立.

i）k=1时，若s(s≥1)是的标准分解式中因子23的指数，即满足23s||F24p.因为24p|242p，由引理1知，得令m=24p，由引理5得由及2s≥s+1可得由引理4得F24m+1≡F24m-1(mod23).因为且23不能整除，所以

ii）设k≥1时，F24kp与的标准分解式中因子23的指数均是s(s≥1).由引理1得所以令m=24k+1p，由引理5得因为且2s≥s+1成立，所以有

定理2假设p为一个不含23和24且大于零的整数，则1是F24p的标准分解式中因子23的指数.

证明因为24|24p，由引理1有F24|F24p，所以F24p≡0(mod23).不妨设p=23m+r，1≤r≤22，则

由232||F24×23得F24p≡F24×23m+1F24r(mod232).232不能整除F24r（1≤r≤24）且23不能整除F24×23m+1，所以232不能整除F24×23m+1F24r.23||F24p成立.所以1是F24p的标准分解式中因子23指数.同理可证定理3.

定理3设p是一个不含23和24且大于零的整数，则2为F24×23p的标准分解式中因子23的指数.

定理4设s是一个整数且s≥0，设p是一个不含23和24且大于零的整数，设n=24×23sp，则标准分解式中因子23的指数是s+1.

证明i）s=0时，n=24p，由定理2知，s+1=1是F24p标准分解式中因子23的指数，所以结论成立.

ii）s=1时，n=24×23p，已知定理2，F24×23p标准分解式中因子23的指数是s+1=2，结论仍成立.

iii）假设s≥1时，的标准分解式中因子23的指数为s+1.下证

令m=24×23sp，由引理2得到式（1），由引理5得到式（2～4）：

由引理6知，

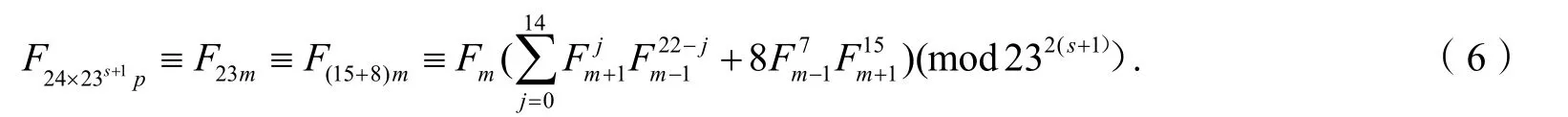
当s≥1时，2(s+1)≥s+3成立.因为24|m，由引理4得Fm+1≡Fm-1(mod23)且其最小非负剩余非0，代入式（6）有

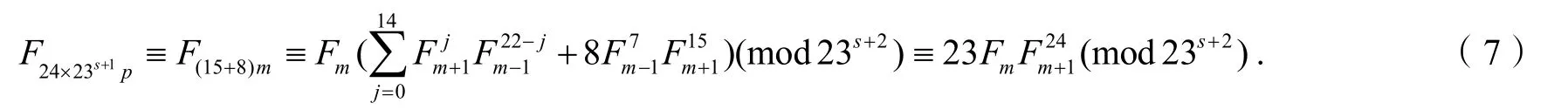
由23s+1||即由式（7）有

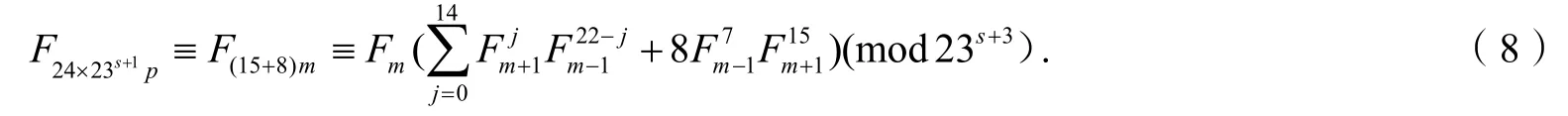
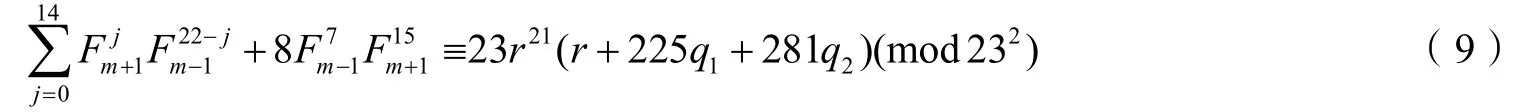
因为23s+1||Fm=Fm+1-Fm-1=23(q1-q2)，所以23s||(q1-q2).由r+225q1+281q2≡r+18(q1-q2)(mod23)知，23不能整除r+225q1+281q2，(r,23)=1，则(r21,23)=1.

由式（9）知232不能整除由式（8）知23s+3不能整除故

3 结论

定理5设k是一个整数且k≥0，设s是一个整数且s≥0，p是一个不含因数23和24且大于零的整数，n为正整数且n=24k×23s×p，则

i）当k=0，0是Fn标准分解式中因子23的指数；

ii）当k≥1，s+1是Fn标准分解式中因子23的指数.

证明i）设k=0.n不能被24整除，引理3得23不能整除Fn，则0是Fn标准分解式中因子23的指数.

ii）设k≥1，定理2得与准分解式中因子23的指数相同，因此仅需讨论k=1.由定理4得标准分解式中因子23的指数是s+1.所以定理5成立.