一类双单叶非-Bazilevi函数类的Fekete-Szeg不等式
梁金荣,郭栋,许庆兵
(滁州职业技术学院 基础部,安徽 滁州 239000)
1 引言
令H表示是单位圆盘内具有下述形式的解析函数类

S表示H中的单叶函数族.
设f(z)和F(z)都是U内满足|w(z)|≤|z|的解析函数w(z),如果f(z)≡F(w(z)),则称f(z)从属于F(z),记作f(z)≺F(z).如果
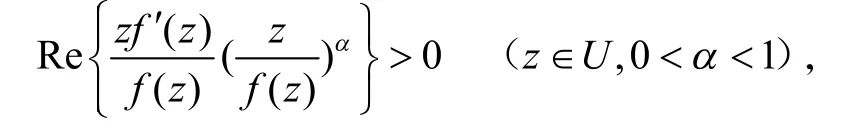
则称f(z)为非Bazilevi函数.此函数类由Obradovic[1]引入研究,后来有些作者证明在α满足一定条件下,此函数类是单叶函数,但时至今日这个问题仍未完全解决.
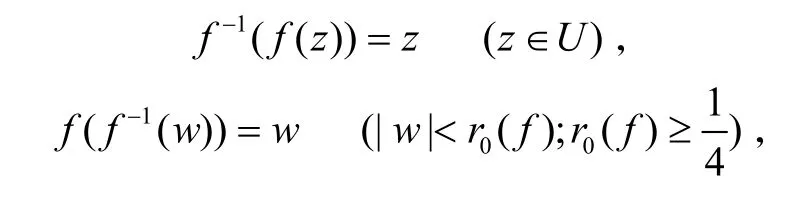
这里
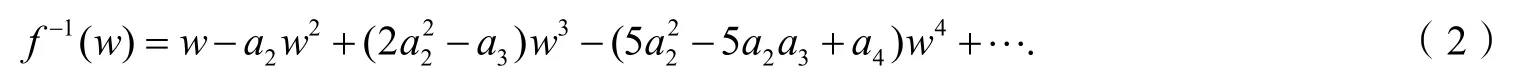
函数f(z)∈A在U内称为双单叶函数当且仅当f(z)和f-1(w)在U内都是单叶函数.现记Σ表示单位圆盘U内所有具有式(1)的双单叶函数.Lewin[2]首先引入了双单叶函数族,证明了f(z)∈Σ,则|a2|≤1.51.随后许多作者[3-6]研究了双单叶函数族的子类|a2|、|a3|的上界问题.Wang等[7]研究了非Bazilevi函数族N(λ,μ,A,B):
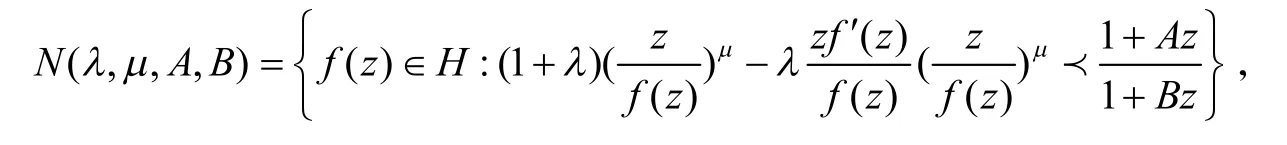
其中λ∈ℂ,0<μ<1,-1≤B<A≤1.
仿照函数类N(λ,μ,A,B)的定义,本文定义了下列双单叶函数类.
定义1令称如果f(z)满足

其中g(w)=f-1(w).为了得出我们的结论,需要下述引理.
引理1[8]设在U内解析,且满足|w(z)|≤|z|,则有

2 主要结果及证明
定理1假设f(z)∈H,由式(1)给出,则有
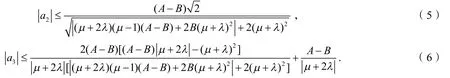
对任意的复数γ,有
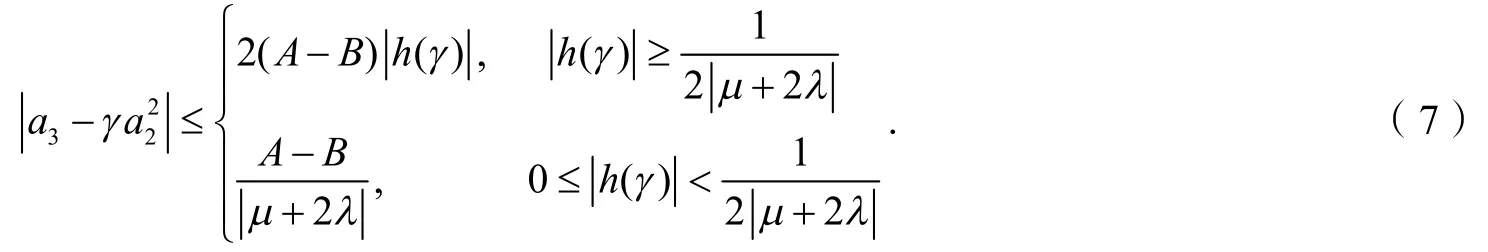
证明因为f(z)∈NΣ(λ,μ,A,B),则存在满足

将u(z)=d1z+d2z2+d3z3+…,v(ω)=c1ω+c2ω2+c3ω3+…代入式(8)、(9),比较z和z2的系数及ω和ω2的系数,得
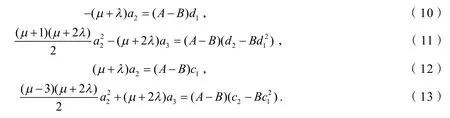
由式(10)和(12)可得

由式(12)和(13)可得

将式(14)、(15)代入式(16),化简可得
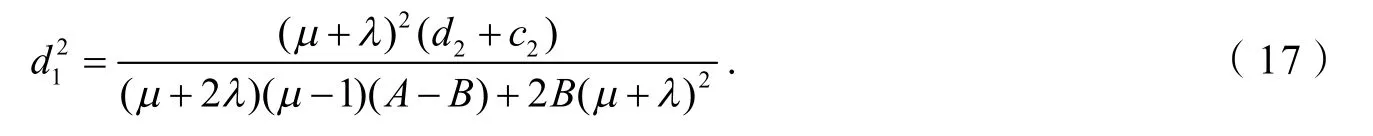
由式(10)和(17)可得

利用引理1及式(10),(14)和(18),可得
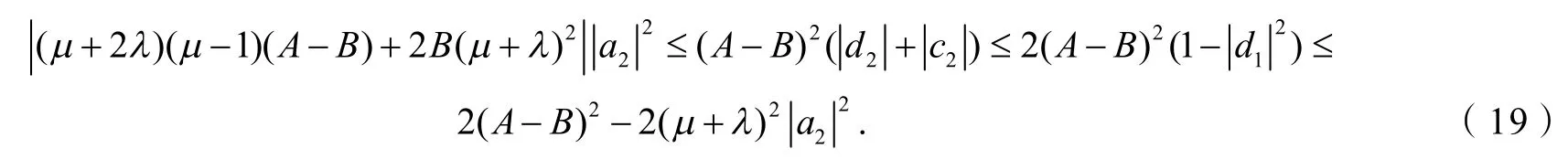
由式(10)和(19)得
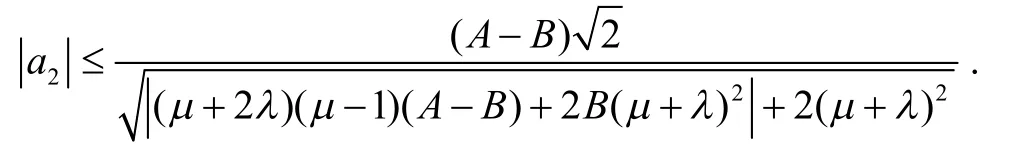
由式(11)和(13)可得

由引理1及式(14)可得
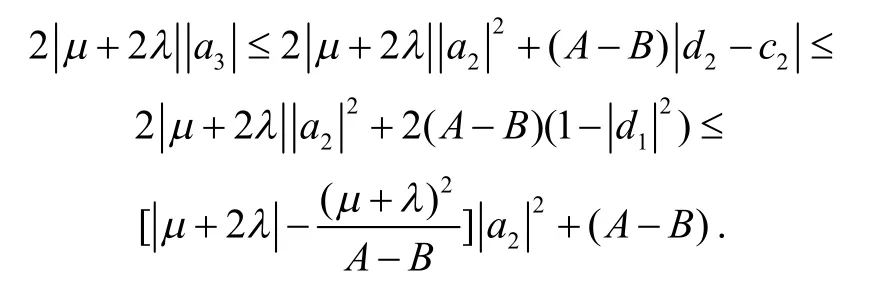
所以
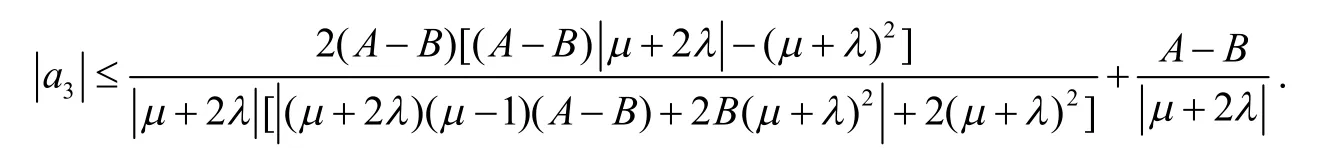
由式(18)和(20)可得
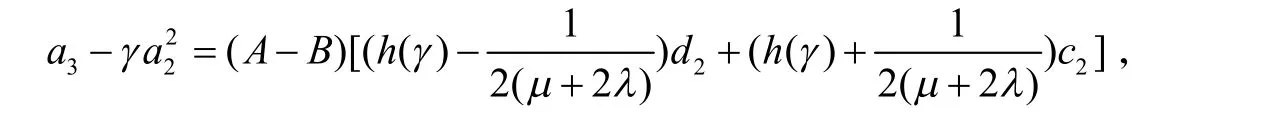
所以由引理得
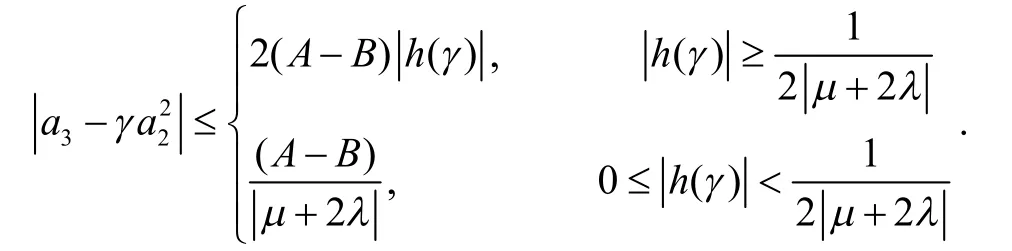
注释:令λ=-1,A=1,B=-1,就得到双单叶非Bazilevi函数族得前两项系数估计及Fekete-Szeg问题


