基于RBF的金属壳谐振陀螺温度误差补偿方法

刘宁 马晓飞 苏中

摘  要： 针对金属壳谐振陀螺由于温度变化导致陀螺精度降低的问题，提出一种基于RBF神经网络的金属壳谐振陀螺温度误差补偿方法。在-4～60 ℃温度范围内，分别建立金属壳谐振陀螺的温度误差一阶多项式模型、二阶多项式模型和RBF神经网络模型，基于三种温度误差模型对陀螺输出进行温度误差补偿。实验数据表明，基于RBF神经网络模型的补偿效果优于基于一阶多项式和二阶多项式模型的补偿效果，补偿后漂移标准差减少了66.31%，可大幅度降低温度变化对金属壳谐振陀螺精度的影响，在工程实际中有一定参考意义。

关键词： 金属壳谐振陀螺; 温度漂移; 温度误差补偿; RBF神经网络; 多项式模型; 漂移标准差

中图分类号： TN37+3?34; V241.5               文献标识码： A                    文章编号： 1004?373X（2019）10?0049?04

Temperature error compensation method based on RBF for metal shell syntonic gyro

LIU Ning1， MA Xiaofei2， SU Zhong1

（1. Beijing Key Laboratory of High Dynamic Navigation Technology， Beijing Information Science & Technology University， Beijing 100101， China;

2. Beijing Institute of Control and Electronics Technology， Beijing 100101， China）

Abstract： A temperature error compensation method based on RBF neural network is proposed for the metal shell syntonic gyro to solve the metal shell syntonic gyro accuracy reduction problem caused by the temperature variation. The first?order polynomial model， second?order polynomial model and RBF neural network model are established respectively in the temperature range of –4～60 ℃ for the temperature errors of the metal shell syntonic gyro. The temperature error compensation is conducted for the gyros output on the basis of three temperature error models. The experimental data shows that the compensation effect of the RBF neural network model is superior to that of the first?order polynomial model and second?order polynomial model; the drift standard deviation after compensation is reduced by 66.31%; the method can significantly decrease the influence of temperature variation on the accuracy of the metal shell syntonic gyro， and has a certain reference value in the engineering practice.

Keywords： metal shell syntonic gyro; temperature drift; temperature error compensation; RBF neural network; polynomial model; drift standard deviation

金属壳谐振陀螺是以金属谐振子作为敏感构件的一种哥氏振动陀螺。其不仅具有传统固体振动陀螺低成本、低功耗、长寿命、高灵敏度的优点，而且还具有结构简单、抗冲击能力强的特点，在兼顾抗过载、量程和精度上表现出了巨大的潜力[1?2]，能够更好地应用在中低精度角速率测量领域[3]。近年来，金属壳谐振陀螺广泛应用于航天、航空、航海等领域。

金属壳谐振陀螺的谐振子由合金材料制成，由于金属材料本身具有较大的温度系数和热膨胀系数，受环境温度变化影响明显[4]。因此，金属壳谐振陀螺对温度非常敏感。当环境温度发生变化时，陀螺的零位漂移明显加剧，陀螺精度大幅下降。因此，对金属壳谐振陀螺的温度特性进行研究，建立陀螺漂移?温度模型，并利用该模型对陀螺输出进行补偿，对于提高陀螺精度有决定性的意义。传统的方法是通过统计方法、模糊算法等手段建立陀螺的近似温度模型，再通过温度传感器测量当前陀螺温度，估算补偿量进行温度补偿[5?6]。文献[7]提出一种无温度传感器的数字温度补偿方案，削弱了温度对金属振动陀螺输出的影响，提高了陀螺漂移等性能指标。文献[8]利用2阶最小二乘方法对金属壳谐振陀螺进行温度零位补偿。传统金属壳谐振陀螺在全温区内对陀螺温度误差进行补偿时，陀螺零偏随温度变化的非线性特点难以得到准确表达，温度误差补偿效果不理想。本文通过对金属壳谐振陀螺温度误差机理进行分析，对金属壳谐振陀螺温度误差补偿方法进行研究，分别采用一阶多项式模型、二阶多项式模型、RBF神经网络模型对金属壳谐振陀螺温度误差进行补偿，经实验验证，RBF神经网络建模补偿效果优于一阶多项式模型和二阶多项式模型，表明了RBF神经网络模型在金属壳谐振陀螺温度误差补偿应用中的有效性。

1  温度误差机理分析

在材料弹性模量变化和热应力作用下，金属谐振子刚度随温度变化的关系可表示为[9]：

[K=K0[1+（kt+λσaE0）（T-T0）]] （1）

式中：[K]，[K0]分别为谐振子在温度[T]，[T0]时的刚度;[kt]为弹性模量随温度变化的系数;[λσ]为热应力引起的谐振子刚度变化的比例系数;[a]为热膨胀系数;[E0]为谐振子材料在温度[T0]时的弹性模量。由此可得，金属谐振子的谐振频率与温度的关系[10]为：

[f（T）=Km          =K0[1+（kt+λσaE0）（T-T0）]m          =f01+（kt+λσaE0）（T-T0）] （2）

式中，[f（T）]，[f0]分别为谐振子在温度[T]，[T0]时的谐振频率。

由此可知，当温度发生变化时，由于金属谐振子的谐振频率发生变化，金属壳谐振陀螺的输出精度降低。

2  多项式模型

多项式模型是基于最小二乘法的线性回归模型，陀螺零偏?温度的多项式模型可表示为：

[B0=a0+a1T+a2T2+…+anTn]  （3）

式中：[B0]为陀螺零偏;[T]为环境温度;[a0]，[a1]，[a2]，…，[an]为拟合系数，可通过最小二乘法拟合确定。

传统金属壳谐振陀螺进行温度误差补偿时多使用一阶多项式模型和二阶多项式模型分别如下：

[B0=a0+a1T]    （4）

[B0=a0+a1T+a2T2]  （5）

3  RBF神经网络模型

人工神经网络（Artificial Neural Network，ANN）是由处理单元广泛互联而成的网络，具有强大的非线性映射能力，因其独特的信息处理能力在模式识别、信息处理、系统建模等领域得到广泛应用。其中，RBF神经网络具有良好的逼近任意非线性函数和表达系统内在的难以解析的规律性的能力，且有极快的学习收敛速度。

RBF神经网络的网络结构如图1所示，它是一种三层前馈网络：第一层为输入层，由信号源节点组成;第二层为隐含层，隐单元数视所描述问题的需要而定，隐单元的变换函数RBF是对称中心径向对称且衰减的非线性函数;第三层为输出层，对输入模式的作用做出响应。

图1  RBF神經网络的网络结构

在RBF神经网络结构中，[X=[x1，x2，…，xn]T]为网络的输入向量，[H=[h1，h2，…，hm]T]为径向基向量，其中[hj]为高斯基函数：

[hj=exp-X-Cj22b2j，   j=1，2，…，m]   （6）

式中：[·]表示欧氏范数;Cj=[cj1，cj2，…，cjm]T为网络第j个节点的中心矢量;网络的基宽向量为B=[b1，b2，…，bm]T，bj为节点的基宽带参数，且大于零。设网络的权向量为W=[w1，w2，…，wm]，则RBF神经网络的输出值为：

[y=WH=w1h1+w2h2+…+wmhm] （7）

4  实验及分析

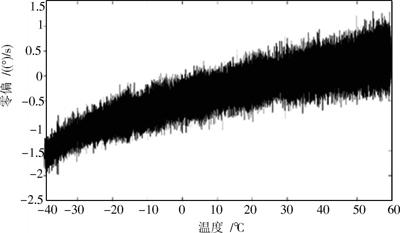
将金属壳谐振陀螺置于温度试验箱内，设置温度试验箱的温度范围为-40～60 ℃，以10 ℃/h的速度进行升温和降温，在温度区间内对陀螺输出进行采样，采样频率200 Hz。数据采集结束后，得到陀螺原始零偏?温度关系如图2所示。

图2  陀螺原始零偏?温度关系

由于陀螺零偏原始数据中样本组数过多，不宜直接进行零偏和温度的拟合。为提高拟合速率和降低测试误差，在陀螺零偏原始数据基础上，-40～60 ℃温度区间内，以0.1 ℃为间隔取点，在每个温度点上取前后100个样本的平均值作为该温度点的陀螺零偏，得到新样本的零偏?温度关系如图3所示。

图3  陀螺新样本零偏?温度关系

基于多项式模型，使用最小二乘法对陀螺零偏?温度新样本拟合，得到零偏随温度变化的一阶多项式模型：

[B0=-0.565+0.017 6T]   （8）

二阶多项式模型：

[B0=-0.491 1+0.019 8T-0.000 1T2]   （9）

基于一阶多项式模型得到的陀螺新样本拟合曲线见图4，基于二阶多项式模型得到的曲线见图5。将陀螺零偏?温度新样本作为学习样本进行训练，基于RBF神经网络模型得到的陀螺新样本拟合曲线如图6所示。

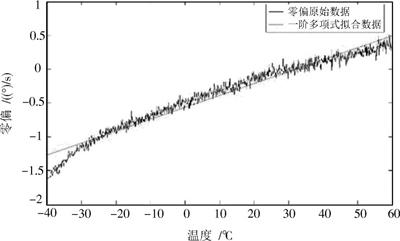
图4  一阶多项式模型拟合曲线

由拟合曲线可看出，基于一阶多项式模型得到的拟合效果最差，基于RBF神经网络模型的拟合效果最优。利用上述三种模型对陀螺零偏原始数据进行补偿，补偿效果分别如图7～图9所示。

对基于三种模型补偿的陀螺零偏数据进行分析比较，比较结果见表1。可以看出，基于一阶多项式模型、二阶多项式模型和RBF神经网络模型对金属壳谐振陀螺进行温度误差补偿后，陀螺的温度漂移得到了抑制，在-40～60 ℃的温度区间内的漂移标准差大幅降低，补偿效果明显。基于RBF神经网络模型的补偿效果最好，补偿后，陀螺漂移最大值降低到0.692 6 （°）/s，标准差降低了66.31%。

图5  二阶多项式模型拟合曲线

图6  RBF神经网络模型拟合曲线

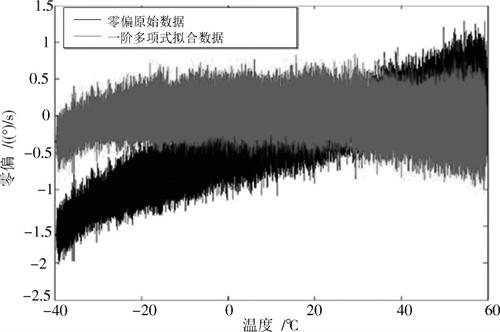
图7  一阶多项式模型补偿效果

图8  二阶多项式模型补偿效果

图9  RBF神经网络模型补偿效果

5  结  论

本文分析了金属壳谐振陀螺的温度误差机理，结合温度实验，建立金属壳谐振陀螺温度误差的一阶多项式模型、二阶多项式模型和RBF神经网络模型，并基于误差模型对陀螺输出零偏进行温度误差补偿。仿真表明，基于RBF神经网络模型的补偿效果优于一阶多项式和二阶多项式模型的补偿效果，补偿后的陀螺输出精度显著提高，补偿效果明显，具有一定的工程应用价值。

参考文献

[1] 谢笛.杯形波动陀螺数字化测控技术研究[D].长沙：国防科技大学，2011.

XIE Di. The study on cupped wave gyro digital measurement and control technology [D]. Changsha： National University of Defense Technology， 2011.

[2] ARMENISE M N， CIMINELLI C， DELL′OLIO F， et al. Advances in gyroscope technologies [M]. Berlin： Springer， 2013.

[3] KRISTIANSEN D. Modeling of cylinder gyroscopes and observer design for nonlinear oscillations [D]. Norway： Norwegian University of Science and Technology， 2000.

[4] LELAND R P. Adaptive tuning for vibrational gyroscopes [C]// Proceedings of the 40th IEEE Conference on Decision and Control. Orlando： IEEE， 2001： 3447?3452.

[5] BATUR C， SREERAMREDDY T， KHASAWNEH Q. Sliding mode control of a simulated MEMS gyroscope [C]// Proceedings of the American Control Conference. Portland： IEEE， 2005： 4160?4165.

[6] FEI J， DING H. Adaptive sliding mode control of dynamic system using RBF neural network [J]. Nonlinear dynamics， 2012， 70（2）： 1563?1573.

[7] LIU N， SU Z， LI Q. Design and experiment of a novel bell?shaped vibratory gyro [J]. Sensors and actuators A： physical， 2016， 238： 37?50.

[8] SHATALOV M Y， LUNIN B S. Vibratory gyroscopes： identification of mathematical model from test data [C]// Proceedings of 14th International Conference on Integrated Navigational Systems. St. Petersburg： [S.l.]， 2007： 1?6.

[9] SU Z， LIU N， LI Q， et al. Research on the signal process of a bell?shaped vibratory angular rate gyro [J]. Sensors， 2014， 14（3）： 5254?5277.

[10] 严恭敏，李四海，秦永元.惯性仪器测试与数据分析[M].北京：国防工业出版社，2012.

YAN Gongmin， LI Sihai， QIN Yongyuan. Inertial device test and data analysis [M]. Beijing： National Defense Industry Press， 2012.