HECC除子标量乘并行集群算法设计
刘海峰 肖超 梁星亮



摘 要: 为了加快超椭圆曲线密码体制(HECC)中除子标量乘的运算速度,进行基于大数据技术的除子标量乘并行算法研究。根据“空间换时间”的策略对除子标量乘法常规方法进行改进,在任务规模为[1016]的条件下,运算耗时减少16.28%,提出基于负载均衡的任务划分优化方案。此方案分别将Hadoop集群平台、Spark集群平台、Spark?GPU集群平台的并行技术应用于改进后的除子标量乘算法中,研究并行算法与串行算法的运行效率。当问题规模一定时,随着节点个数的增加,不同集群平台的加速呈上升趋势,其中Spark?GPU并行算法的增长趋势最为明显,当节点个数为4时,Spark?GPU并行算法的加速比达到了261.84。通过对比3种集群平台的并行算法,发现Spark?GPU可以最有效地缩短运算耗时,加快除子标量乘法的运算速度。
关键词: 超椭圆曲线密码体制; 除子标量乘; 并行计算; 集群平台; Spark?GPU; Hadoop
中图分类号: TN929.52?34; TP393.08 文献标识码: A 文章编号: 1004?373X(2019)10?0023?04
Design of divisor scalar multiplication parallel clustering algorithm for HECC
LIU Haifeng, XIAO Chao, LIANG Xingliang
(School of Arts & Sciences, Shaanxi University of Science & Technology, Xian 710021, China)
Abstract: A divisor scalar multiplication parallel algorithm based on the big data technology is studied to speed up the operation rate of the divisor scalar multiplication in the hyperelliptic curve cryptosystem (HECC). The conventional method of the divisor scalar multiplication is improved according to the "space?for?time" strategy, whose operation time computation is reduced by 16.28% under the condition that the task scale is 1016. A task partition optimization scheme based on load balancing is proposed. The operation efficiencies of the parallel algorithm and serial algorithm are studied by applying the parallel technologies of the Hadoop cluster platform, Spark cluster platform and Spark?GPU cluster platform to the improved divisor scalar multiplication algorithm. When the problem scale is fixed, the acceleration of different cluster platforms emerges in an upward trend with the increase of node quantity, in which the growth trend of the Spark?GPU parallel algorithm is the most obvious, and the speed?up ratio of the Spark?GPU parallel algorithm can reach 261.84 when the node quantity is 4. By comparing the parallel algorithms of three cluster platforms, it is found that the Spark?GPU parallel algorithm can most effectively reduce the operation time consumption and speed up the operation rate of divisor scalar multiplication.
Keywords: HECC; divisor scalar multiplication; parallel calculation; cluster platform; Spark?GPU; Hadoop
0 引 言
随着多核时代的到来,并行计算成为提高算法效率的主流技术之一。Hadoop的计算模型比较简单,适合数据量大但核心计算并不复杂的处理作业;而对于较复杂的计算模型,尤其是循环、迭代任务的处理效率欠佳。基于内存计算的并行计算框架Spark,对于复杂的大规模计算任务实现轻量级快速处理,可以高效地解决频繁迭代问题。
在如今的计算机网络环境下,密码技术已经成为安全通信的关键手段。1989年,Neal Koblitz首次提出了超椭圆曲线密码体制(HECC)的理论,作为椭圆曲线密码体制(ECC)理论的推广[1]。与ECC相比,HECC安全性高、所需的基域更小,特别适合在受限系统中使用。然而,除子标量乘的运算速度直接影响HECC的总体实现效率,成为HECC的“瓶颈”问题[2]。杨怡琳主要对偶特征域上的超椭圆曲线进行了深入的研究,推导出了亏格为2的除子二分算法过程[3]。范欣欣从群运算的明确公式、标量乘算法的角度对影响HECC性能的诸多因素进行了优化实现。但基本上都是一些针对除子标量乘的理论研究层面的串行算法,而基于集群平台的并行算法研究却相对较少。因此,本文分别将Hadoop,Spark以及Spark?GPU的大数据并行处理技术应用到HECC的除子标量乘运算中,研究并行算法与串行算法的运行效率。
1 超椭圆曲线密码体制的数学理论
设[Fq]是有限域[Fq]上的一个闭包,则[Fq]上的超椭圆曲线[C]的[Weierstrass]方程为:
[C: y2+h(x)y=f(x)] (1)
式中:定义[g]为超椭圆曲线[C]的亏格;[h(x)]是次数不大于[g]的多项式;[f(x)]是次数为[2g+1]的首一多项式,且[h(x),f(x)∈Fq]。特别地,当[g=1]时,超椭圆曲线[C]退化为椭圆曲线[4]。
一个除子[D]由曲线[C]上若干点求和取得:
[D=P∈CmpP, mp∈Z] (2)
设[Dn]表示[C]上所有除子的集合,则[Dn]在式(3)规则下形成一个加法群[5]。
[P∈CmpP+P∈CnpP=P∈C(mp+np)P] (3)
曲线[C]上的[Jacobian]商群记为[J(F)=D0P],商群上的除子标量乘,即
[mD=D+D+…+Dm] (4)
2 除子标量乘算法改进方案
在超椭圆曲线密码体制中,密码学的核心问题是除子标量乘问题,直接影响整个密码体制的实现效率[6]。采用常规循环计算除子标量乘,需要进行[m]次除子加法,与[m]联系密切。当[m]为一个大整数时,计算效率低。因此,需要进行改进。将[m]描述为[s]进制的表示形式。
[m=an-1sn-1+an-2sn-2+…+a1m+a0] (5)
为了减少选取除子倍加算法的次数,选择适当的正整数[k≥1],令[s=2k],[n=kN],则除子标量乘[mD]表示为:
[mD=i=1N-1(ai2ki)D =2k(2k…(2k(O+aN-1D)+aN-2D)…+a1D)+a0D] (6)
则迭代格式为:
[T(i)=2kT(i-1)+aN-iD, i=1,2,…,NT(0)=O] (7)
对于[2kT(i-1)],每一轮需要[k]次除子倍加运算;对于[aN-iD],首先将[aN-i]表示为[p]位二进制形式[aN-i=(bpbp-1…b1)2],则当[aN-i≠0]时,每一轮需要[k]次除子倍点运算,需要[aN-i]次除子加法运算。由于每一轮需要重复计算[aN-iD],消耗了大量的计算时间,需要进一步改进。
因為[aN-i∈{0,1,2,…,2k-1}],需要计算[2D,][3D,…,(2k-1)D]。其中,[(i+1)D=iD+D,i=1,2,…,2k-2]。采用“以空间换时间”的基本思想,将[2D,3D,…,(2k-1)D]的计算结果预先存储在[U[1],U[2],…,U[2k-1]]中,减少时间开销。
改进后的算法共需要[2k+nk+n-1]次除子加法运算,需要[n]次除子倍加运算。研究发现,一次除子倍加耗时约为除子加法的[12],则时间复杂度为[f(k)=2k+nk+32n-1]。改进后算法的运算量[f(k)]远远小于常规循环的计算量[m],说明改进后算法大大减小了计算量。对[f(k)]求导,令[f′(k)=2kln 2-nk2=0],得到[n=2kk2ln 2]。可以看出,当加密密钥的长度[n]为48~96位之间时,[k=3]时,最接近50,算法的效率达到最佳。
3 除子标量乘并行算法设计
3.1 基于负载均衡的子任务划分方案优化设计
为达到负载均衡,计算[mD]时,将大整数[m]均匀分割成[p]个子任务。假设[subtaski]代表划分后的子任务规模,前[p-1]个子任务规模均为[x],[subtaskp]为[y],将最优方案表示为[x*,y*],则需要求解如下整数优化问题:
[minx-y(p-1)x+y=mx,y∈Z*] (8)
通过求解该优化问题,得到改进后的划分方案为:[x*=mp+1, mp-mp≥0.5mp, 其他] (9)
[y*=m-(p-1)x*] (10)
3.2 基于Hadoop,Spark,Spark?GPU的除子标量乘并行化设计
利用Hadoop并行集群平台进行除子标量乘算法并行化设计,主要流程如下:
1) 从HDFS上获取大整数[m]、除子[D];
2) 初始化除子标量乘的存储单元T,创建用于计算除子标量乘的工作单元DSMJob;采用基于负载均衡的子任务划分优化方案对大整数[m]进行划分,并且将划分后的子任务[(subtaski)D]分发给[Mapi];
3) [Mapi]根据改进后的除子标量乘算法,对于子任务进行计算:
① 已知子任务的加密密钥长度[n],根据[n=2kk2ln 2],估计得到最佳参数[k];
② 将[2D,3D,…,(2k-1)D]的计算结果预先存储在数组U中;
③ 进行计算除子标量乘的迭代运算,迭代完成后得到[Mapi]的计算结果[(subtaski)D]。
4) 将计算后的结果通过Reduce进行汇总合并,得到最终需要的除子标量乘算法结果,即
[mD=T=i=1p(subtaski)D]
利用Spark并行实现除子标量乘,总体上也是采用“Map”和“Reduce”的思想。然而,与Hadoop不同的是,针对所有子任务,Hadoop与磁盘进行多次交互,而Spark在内存中对弹性分布式数据集RDD进行计算,中间不需与磁盘交互[7]。
基于CPU与GPU混合并行计算系统已经逐渐成为国内外高性能计算领域的热点研究方向。利用GPU强大的并行处理能力,结合Spark并行集群平台,可以大幅度提升计算性能[8]。CPU与GPU混合并行计算框架如图1所示。

图1 CPU与GPU混合并行计算框架
基于Spark?GPU集群平台的除子标量乘并行算法计算流程如下:
1) CPU根据计算资源分布情况以及负载均衡机制,向各worker节点分配子任务。worker节点接收到程序指令和任务分配信息后,将操作指令传递到GPU,以线程为单位计算除子标量乘。每个节点计算完成后,将计算结果保存在显存[9]。
2) 在Spark集群平台中,显存的计算结果以特定的形式转化为RDD数据块,Reduce将所有worker节点求和汇总。
4 实验设计与分析
本实验平台的集群由1个控制节点和4台计算节点组成,所有节点配置都相同,有4核CPU(主频:1.80 GHz)、8 GB内存和60 GB硬盘,控制节点和计算节点间以速度约为10 Mb/s的10Base?T以太网互联。Hadoop的版本为2.6.0,Spark的版本为1.6.1,Hadoop程序使用java编写,java版本为1.7,Spark程序使用scala编写,版本为2.10.6。
设[Cp]是有限域[Fq]上的超椭圆曲线,且[p=1019+51],超椭圆曲线[C]的表示形式如下:
[C:y2=x5+3 141 592 653 589 793 238x4+ 4 626 433 832 795 028 841x3+971 639 937 510 582 097x2+ 49 445 923 078 164 062 986x+2 089 986 280 348 253 421]
此曲线的阶为:
9 999 999 998 287 192 967 145 227 700 028 166 080
設[a(x)=x3+x2+2,b(x)=6x2+6x],则[D=a(x),b(x)∈JCq(Fq)]。为了便于研究不同问题规模下算法的时间效率,设置3组计算任务[miD],[mi]分别为[104,1010,1016]。分别基于3种不同平台进行并行计算,并行的计算节点为1 节点、2 节点、3 节点、4 节点。采用改进算法对计算任务[miD]进行测试,记录运行时间。共进行4类实验:
实验1:基于普通平台的改进算法测试,与常规算法进行对比;
实验2:基于Hadoop平台的改进算法测试;
实验3:基于Spark平台的改进算法测试;
实验4:基于Spark?GPU平台的改进算法测试。
基于普通平台的改进算法与常规算法的耗时比如图2所示。

图2 算法改进前后的耗时比
观察图2发现,随着任务规模的增加,耗时比逐渐增大,当任务规模为[1016]时,耗时比达到了1.195。
以任务规模为[1010]的情况为例,研究不同节点个数时,3种平台的加速比随着节点个数的变化趋势如图3所示。

图3 不同节点个数的加速比
以节点数N=2为例,研究不同任务规模时,3种平台的加速比随着问题规模的变化趋势如图4所示。
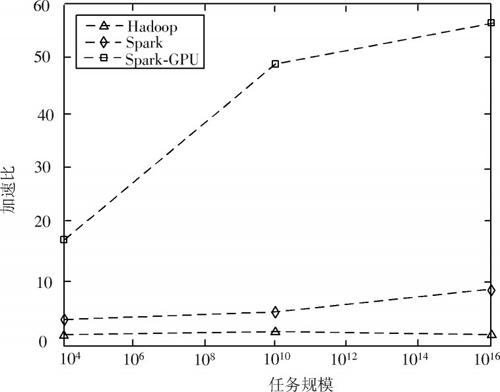
图4 不同任务规模的加速比
由图3可知,在相同问题规模情况下,随着节点个数的增加,不同平台的加速比也逐渐增加。基于Spark?GPU集群平台进行并行计算时,加速比增长最为明显。当节点个数为4时,基于Spark?GPU集群平台并行算法的加速比达到了261.84。
由图4可知,在相同数量节点情况下,随着问题规模的增长,加速比曲线随着问题规模增加逐渐上升。其中,基于Spark?GPU并行算法加速比增长最为明显。当问题规模为[1016]时,Spark?GPU对应的加速比达到了56.19。
5 结 论
通过4组实验,可以得到如下结论:
1) 根据改进后算法和常规算法的耗时比,说明改进后的算法缩短了计算时间,提高了运算效率;
2) 通过研究不同节点个数时,3种平台的加速比随着节点个数的变化趋势,发现随着节点个数的增加,不同平台的加速比也逐渐增加,且基于Spark?GPU平台的并行算法加速比增长最为明显;
3) 通过研究不同问题规模时,3种平台的加速比随着问题规模的变化趋势,发现加速比曲线随着问题规模增加逐渐上升。
参考文献
[1] KOBLITZ N. Hyperelliptic cryptosystems [J]. Journal of cryptology, 1989, 1(3): 139?150.
[2] KOBLITZ N. A family of Jacobians suitable for discrete log cryptosystems [C]// Proceedings of Conference on the Theory and Application of Cryptology. New York: Springer, 1990: 94?99.
[3] 杨怡琳.超椭圆曲线上快速标量乘算法研究[D].杭州:杭州电子科技大学,2014.
YANG Yilin. Research on fast scalar multiplication algorithm on hyperelliptic curves [D]. Hangzhou: Hangzhou Dianzi University, 2014.
[4] 郝艳华,范欣欣,王育民.亏格为3的超椭圆曲线除子加法的并行算法[J].计算机科学,2007,34(8):114?119.
HAO Yanhua, FAN Xinxin, WANG Yumin. Parallelizing explicit formula in Genus 3 hyperelliptic curves [J]. Computer science, 2007, 34(8): 114?119.
[5] 朱艳蕊.超椭圆曲线标量乘快速算法研究[D].成都:西南交通大学,2013.
ZHU Yanrui. Research on fast algorithm of superelliptic curve scalar multiplication [D]. Chengdu: Southwest Jiaotong University, 2013.
[6] 游林.一类超椭圆曲线上的快速除子标量乘[J].电子学报,2008,36(10):2049?2054.
YOU Lin. Fast divisor scalar multiplications on a class of hyperelliptic curves [J]. Acta electronica sinica, 2008, 36(10): 2049?2054.
[7] 李建江,崔健,王聃,等.MapReduce并行编程模型研究综述[J].电子学报,2011,39(11):2635?2642.
LI Jianjiang, CUI Jian, WANG Dan, et al. Survey of MapReduce parallel programming model [J]. Acta electronica sinica, 2011, 39(11): 2635?2642.
[8] 江小平,李成华,向文,等.K?means聚类算法的MapReduce并行化实现[J].华中科技大学学报(自然科学版),2011,39(z1):120?124.
JIANG Xiaoping, LI Chenghua, XIANG Wen, et al. Parallel implementing of K?means clustering algorithm using MapReduce programming mode [J]. Journal of Huazhong University of Science and Technology (Natural science), 2011, 39(S1): 120?124.
[9] 周情涛,何军,胡昭华,等.基于GPU的Spark大数据技术在实验室的开发应用[J].实验室研究与探索,2017,36(1):112?116.
ZHOU Qingtao, HE Jun, HU Zhaohua, et al. Department and application of the GPU?based Spark big data technology in laboratory [J]. Research and exploration in laboratory, 2017, 36(1): 112?116.
[10] 杨冬进,娄建安,黄天辰.锂电池内阻测量的电路设计及其算法仿真[J].电子设计工程,2017,25(24):129?133.
YANG Dongjin, LOU Jianan, HUANG Tianchen. The circuit design of lithium battery internal resistance measurement and algorithm simulation [J]. Electronic design engineering, 2017,25(24): 129?133.

