基于变值逻辑理论的心音信号一维可视化研究
刘翔 孙静 王威廉


摘 要: 心脏听诊在心脏病初期诊断方面具有重要意义,国内外对心音信号从信号的角度分析已经做了大量的研究。文中将传统的心音信号经过预处理后,对提取的信号包络进行一系列的逻辑变换,最后通过一维数据处理将其制成一维折线图。在保持原信号特征基本不丢失的情况下,将其反映在一维折线图中,从而可以直接观察到不同病理性心音信号在对应的一维折线图中所表现出的不同特征。实验结果表明,该方法可以有效显示出心音信号的特征,能够较好地区分正常与病理性心音信号。
关键词: 心音信号分析; 包络提取; 可视化设计; 逻辑变换; 一维折线图; 心脏听诊
中图分类号: TN27?34 文献标识码: A 文章编号: 1004?373X(2019)10?0010?05
Research on one?dimensional visualization of heart sound signal based on
variable?value logic theory
LIU Xiang, SUN Jing, WANG Weilian
(School of Information Science & Engineering, Yunnan University, Kunming 650091, China)
Abstract: The cardiac auscultation plays an important role in the early diagnosis of the heart disease, and a lot of heart sound signal analysis research has been done from the perspective of signal at home and abroad. Therefore, a series of logical transformations are conducted for the extracted signal envelopes after the preprocessing of the traditional heart sound signals in this paper. A one?dimensional line chart is made for heart sound signals by means of one?dimensional data processing. The heart sound signals are reflected in the one?dimensional line chart in the condition that the original signal characteristics are not substantially lost, so as to directly observe different pathological heart sound signals′ characteristics represented in the corresponding one?dimensional line chart. The experimental results show that the method can effectively display the characteristics of heart sound signals, and can distinguish normal and pathological heart sound signals well.
Keywords: heart sound signal analysis; envelope extraction; visualization design; logical transformation; one?dimensional line chart; cardiac auscultation
0 引 言
先天性心脏病是心脏器质类疾病,目前它的初步诊断方式是心音听诊,确诊由心脏彩超完成。心音听诊是由专业的医务人员借助心音听诊器来进行听诊,听诊结果会受到听诊人主观的影响,容易造成误诊,尤其对于分布在医疗水平偏低的边远地区的患者来说,只能通过心音听诊来进行筛查,更加容易出现误诊[1]。心音信号包含了大量的人体心脏的病理信息,能够反映心脏当前状况。因此,对心音信号进行分析对于诊断与心脏有关的疾病有重要的意义,而且可以为临床诊断提供一定参考。
目前,心音信号的分析方法多为传统的信号分析方法,本文介绍一种全新的基于变值逻辑理论的信号分析方法。根据序列密码分析模式正在发展的一类原创型的连续信号分析技术,对传统的心音信号进行转换,将其通过一维折线图的方式展现出来,通过比较不同病理性心音信号转换生成的一维折线图来进行分析识别,为心音信号的分析识别提供了新的思路。
1 心音信号变值逻辑理论分析系统结构
心音信号变值逻辑理论分析系统主要包括心音信号去噪、包络提取、变值逻辑数据计算及可视化设计。其中变值逻辑数据计算又分为基础值计算、范围值计算、伪DNA序列映射、0?1序列转换和测度统计等模块。本文心音信号去噪方法采用小波软阈值去噪[2],包络提取采用希尔伯特?黄变换[3]方法提取心音信号的包络,在包络提取的基础上进行数据计算和可视化研究。
2 心音信号去噪及包络提取
2.1 心音信号去噪
心音信号是一种微弱的生理信号,在采集时很容易受到噪声干扰[4],因此,要对采集到的心音信号进行去噪,尽可能地保留信号中有用的成分。通过实验发现,小波基函数和分级层数的选择对去噪结果有很大影响[5],通过实验对比发现,选用小波coif3[6]为小波基,选用5层小波分解层数。小波阈值去噪法涉及到软阈值和硬阈值的选择。由于软阈值去噪可以保证小波系数的符号不变,使输入/输出曲线是连续的,同时更易于处理,不会引起重构信号的振荡[7]。因此,本文选取软阈值方法。
2.2 心音信号包络提取
常用的心音包络提取有希尔伯特?黄变换方法和归一化香农能量[8]方法。归一化香农能量提取的包络会对信号进行压缩,容易损失较多的有效信息。本文是在心音信号包络基础上进行的分析识别,需要提取的包络保留较多的有效信息,经过试验结果对比发现,通过希尔伯特?黄变换提取的心音信号包络没有其他方法光滑,但却保留了更多的有效信息,故本文采用希尔伯特?黄变换方法提取包络。
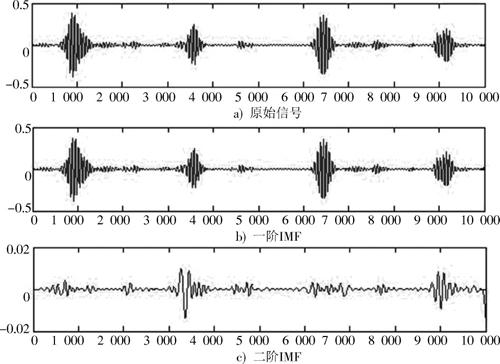
希尔伯特?黄变换(Hilbert?Huang transform,HHT),是由经验模态分解(EMD)和希尔伯特变换两部分组成[9]。经验模态分解即将任意一个复杂的信号分解为一系列固有模态函数(IMF)[10],滤波后的心音信号使用经验模态方法分解,经过两次分解之后,剩余的残差对原信号意义不大,因此本文进行了两层分解。分解后得到的IMF如图1所示。
希尔伯特变换公式为:
[Hxt=1π-∞+∞xττ-tdτ=xt?1πt] (1)
式中:[x(t)]为听诊器记录的一个心音信号,该变换采用积分的原理;“*”表示卷积运算符。
对第一阶IMF进行希尔伯特变换,得到的希尔伯特包络如图2所示。
3 变值逻辑数据计算
3.1 变值逻辑理论
变值逻辑理论体系是在经典的变值逻辑空间的基础上进行扩展演变而来的。传统的逻辑映射关系中包括“与”“或”“非”三种基础逻辑运算,在这三种逻辑运算的基础上,又新增了“置换”和“互补”两种运算[11],从而扩充了逻辑函数空间。根据这一思想,对具体实验信号进行数据转换,从而实现可视化研究[12]。

图1 心音信号的二阶IMF

图2 心音信号一阶IMF及其希尔伯特包络
3.2 变值逻辑数值计算结构
心音信号变值逻辑数据分析结构如图3所示。

图3 变值逻辑数据分析结构图
3.3 基础值计算
基础值计算模型是将连续的心音信号数据序列 [a0,a1,a2,…,an]通过公式(2)进行计算,获得相对应的基值序列BV[bv0,bv1,bv2,…,bvn-w+1]。基础值计算公式如下:
[ bvj=1wi=jw+j-1aij=0,1,2,…,n-w+1;i=j,j+1,j+2,…,n] (2)
式中[w]為滑动窗口值,这里取[w=4]。
3.4 范围值计算
范围值计算模型通过公式(3)计算范围值序列RV[rv0,rv1,rv2,…,rvn-w+1],范围值计算公式如下:
[rvj=s2maxaj,aj+1,aj+2,…,aj+w-1- minaj,aj+1,aj+2,…,aj+w-1j=0,1,2,…,n-w+1] (3)
式中:[maxaj,aj+1,aj+2,…,aj+w-1]表示包含在滑动窗口内的心音数据序列的最大值;[minaj,aj+1,aj+2,…,aj+w-1]表示包含在滑动窗口内的心音数据序列的最小值;[s]为稳定区间值,是一个临界参考点,这里取0.95。
3.5 伪DNA序列映射
3.5.1 区间取值计算
区间取值计算模型通过公式(4)计算区间值序列RC[c0,c1,c2,…,cn-w+1],区间取值计算公式如下:
[cj=aj-bvjs*rvj, j=0,1,2,…,n-w+1] (4)
式中[s]为稳定区间值。
3.5.2 伪DNA序列
通过式(2)~式(4)三个计算模型的处理,已经将传统的心音信号序列转换为与之对应的区间取值序列,根据选取的区间范围参数,可将不同的区间取值转换为对应的不同伪DNA值,进而转换成对应的伪DNA序列DV[dv0,dv1,dv2,…,dvn-w+1]。区间范围参数选取为:
[dvk=A, cj≥sB, 0≤cj≤sC, -s≤cj≤0D, cj≤-s j=0,1,2,…,n-w+1] (5)
式中:[s]为稳定区间值;A,B,C,D为转换出的4个伪DNA元素,心音信号转换出的伪DNA序列由这4个元素组成。试验结果表明,根据具体波形的不同,其映射出的伪DNA元素有很大差别,其中波形上升和下降较为陡的波形将分别映射成A和D,而较为平缓的波形则分别映射成B和C。
3.6 0?1序列转换
将前面转换得到的伪DNA序列,通过标记不同的伪DNA元素,将其转换成对应的0?1序列[13]。由于心音信号包络的波峰较多,按照理论研究来说,其转换出的伪DNA序列中A和B元素应该较多,而实际实验也验证了这一点。故本文选取A作为标记元素,将伪DNA序列转换为A所对应的0?1序列R[r0,r1,r2,…,rn-w+1],转换公式如下:
[rl=0, dvk≠p1, dvk=p,p∈A,B,C,D;k=0,1,2,…,n-w+1] (6)
3.7 测度统计
3.7.1 变值状态划分
对于转换出的0?1序列进行测度统计前,首先要根据数据长度和数据特点进行分段, 然后根据分段结果,对相邻两个分段区间内的对应位置的数据进行变值状态划分,设分段段长为[m],第[n]段的数据为[xi],其相邻的第[n+1]段的数据为[yi],则根据测度划分规则,将其划分成变值逻辑空间中4种变值状态,具体划分规则如下:
[T=00, xi=0,yi=001, xi=0,yi=110, xi=1,yi=011, xi=1,yi=1] (7)
3.7.2 测度概率统计
根据已经划分好的变值状态,分别统计出各个分段中4种变值状态的个数,然后计算各分段对应的测度向量,计算公式如下:
[P00=N00m;P01=N01m;P10=N10m;P11=N11m;P0=N00+N01m;P1=N10+N11m;Pn00=P00P0;Pn01=P01P0;Pn10=P10P1;Pn11=P11P1]
式中:[P00,P01,P10,P11]定义为非归一化方法下的测度;[P0,P1,Pn00,Pn01,Pn10,Pn11]定义为归一化方法下的测度。
4 可视化设计
由于心音信号为一串连续的信号,故需要对选取的一维测度进行进一步处理,使其能够反映心音信号的连续性。本文在传统的散点数集统计分析方法(PMF和CDF模型[14])的基础上,根据心音信号的特点,提出累积概率质量函数模型和方差连续分布函数模型。本文选取[P01]为一维可视化测度。
4.1 累积概率质量函数模型
由于心音信号为连续的非平稳信号,从生理上分析可知,心音信号每个采样点的数值与其前面的数据有一定的内在联系,故要对选取的测度进行累积,使其能够充分地反映心音信号这一特点。该模型主要反映前[i]个分段组成的散点子集的离方差值的累积变化情况,具体公式为:
[AFi=ei, i≤1] (8)
式中,[ei]为第[i]个分段点对应于该测度点集的离均差。
4.2 方差连续分布函数模型
该模型主要反应前[i]个分段组成的散点子集的方差值的累积变化情况,公式为:
[VFi=1ie2i, i≤1] (9)
5 实验结果及结论
选取实验室采集的质量较好的心音数据分别进行绘制,实验结果见图4、图5。
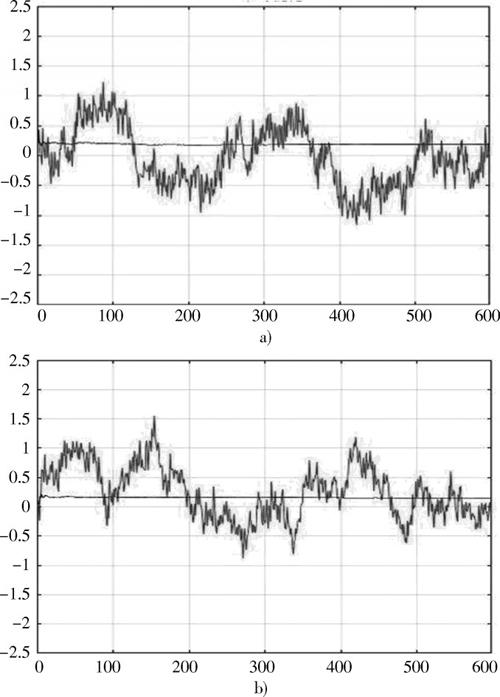
图4 正常人心音信号一维折线图

图5 病理性心音信号一维折线图
图4为正常人心音信号一维折线图,图5为病理性心音信号一维折线图。从图中可以看出,正常人心音信號的一维折线图较为平缓,而病理性心音信号的一维折线图波动较大,通过对比可以看出病理性心音信号与正常人心音信号明显不同。后续的实验中,在实验室采集的心音信号数据中符合上述特征的占总体的70%以上,就目前初步的实验结果来看,其余未符合该特征的数据可能是由于不同病种的特征不一致所导致,与心音信号的采集质量也有一定的关系。
6 结 语
本文采用变值逻辑理论对心音信号进行分类识别,具有一定的可行性,为后续的先天性心脏病不同病种的分类识别提供了一定的实验及理论基础,具有继续深入研究的价值。
注:本文通讯作者为孙静。
参考文献
[1] 刘朝辉,冯国军,梁坤,等.超声心动图对心脏听诊有杂音的脑瘫儿童先天性心脏病筛查[J].中外医学研究,2015,13(18):54?55.
LIU Chaohui, FENG Guojun, LIANG Kun, et al. Congenital heart disease screening by ultrasonic cardiogram for cerebral palsy children with cardiac souffle in cardiac auscultation [J]. Chinese and foreign medical research, 2015, 13(18): 54?55.
[2] 柯水霞,李迟生.基于LMS自适应噪声抵消和小波阈值的语音降噪算法研究[J].现代电子技术,2016,39(3):27?29.
KE Shuixia, LI Chisheng. Research on speech denoising algorithm based on LMS adaptive noise cancellation and wavelet threshold [J]. Modern electronics technique, 2016, 39(3): 27?29.
[3] 聂杰文,徐明强,王树青.基于小波消噪和希尔伯特黄变换的损伤检测技术研究[J].中国海洋大学学报(自然科学版),2016,46(4):142?148.
NIE Jiewen, XU Mingqiang, WANG Shuqing. Research on structural damage detection based on wavelet denoising and Hilbert?Huang transform [J]. Periodical of Ocean University of China, 2016, 46(4): 142?148.
[4] 任浩冉.基于手机的心音采集系统的方法研究[D].秦皇岛:燕山大学,2016.
REN Haoran. Research of the method of heart sound acquisition system based on mobile phones [D]. Qinhuangdao: Yanshan University, 2016.
[5] 刘淑聪,高尔根,陈逊,等.小波包多阈值法在地震信号去噪中的应用研究[J].现代电子技术,2015,38(23):54?59.
LIU Shucong, GAO Ergen, CHEN Xun, et al. Application of wavelet packet multi?threshold method in seismic signal denoising [J]. Modern electronics technique, 2015, 38(23): 54?59.
[6] 孟慧,梅铁民,朱向荣.一种小波包变换的声纹参数提取方法研究[J].沈阳:沈阳理工大学学报,2015,34(6):77?82.
MENG Hui, MEI Tiemin, ZHU Xiangrong. Voiceprint parameters extraction based on wavelet packet transform [J]. Transactions of Shenyang Ligong University, 2015, 34(6): 77?82.
[7] 秦国瑾,吴昭萍,王馨平,等.基于小波变换的呼吸音降噪新方法研究[J].现代电子技术,2016,39(3):18?22.
QIN Guojin, WU Zhaoping, WANG Xinping, et al. Research on wavelet transform based new denoising methods for respiratory sound [J]. Modern electronics technique, 2016, 39(3): 18?22.
[8] 李晓玉.基于包络提取的心音信号分段算法的研究[D].杭州:浙江大学,2015.
LI Xiaoyu. Research on heart sound signal segmentation algorithm based on envelope extraction [D]. Hangzhou: Zhejiang University, 2015.
[9] 杜建卫.希尔伯特黄变换方法及其在特征提取中的应用研究[D].北京:北京科技大学,2017.
DU Jianwei. Hilbert Huang transform and its application in feature extraction [D]. Beijing: University of Science and Technology Beijing, 2017.
[10] 李光辉.基于希尔伯特黄变换及其改进方法的信号分析研究与应用[D].成都:成都理工大学,2012.
LI Guanghui. Research and application of signal analysis based on Hilbert yellow transform and its improvement method [D]. Chengdu: Chengdu University of Technology, 2012.
[11] 郑智捷.多元逻辑函数的基础等价变值表示[J].云南民族大学学报(自然科学版),2011,20(5):396?397.
ZHENG Zhijie. Equivalent expressions of multiple?variable logic and variant logic functions [J]. Journal of Yunnan University Nationalities (Natural sciences edition), 2011, 20(5): 396?397.
[12] 李天宇.伪随机序列分段变值测量二维可视化[D].昆明:云南大学,2015.
LI Tianyu. Two?dimensional visualization of segmented variable?value measurement using pseudo?random sequence [D]. Kunming: Yunnan University, 2015.
[13] 王安,宋靜,任仲夷,等.一种新型变值逻辑伪随机数发生器的实现与分析[J].云南大学学报(自然科学版),2013,35(z2):120?124.
WANG An, SONG Jing, REN Zhongyi, et al. Implementation and analysis of a new variant logic pseudo?random number generator [J]. Journal of Yunnan University (Natural sciences), 2013, 35(S2): 120?124.
[14] 肖薇薇,许晶晶.基于累积分布函数的统计降尺度模型校验方法适用性研究[J].江西农业学报,2016,28(1):74?78.
XIAO Weiwei, XU Jingjing. Applied research of calibration method for SDSM model based on cumulative distribution function [J]. Acta agriculturae Jiangxi, 2016, 28(1): 74?78.

