多尺度自适应直接信息采样与重构
李 成,晋玉猛,田文飚
(1.91001部队,北京100036;2.中国新兴铸管股份有限公司,河北邯郸056300;3.海军航空大学,山东烟台264001)
如今,许多信号宽带较大,常规采样器件可能有采集压力,但在典型应用中这些信号的“信息速率”通常很小。近年来,在压缩感知[1-4](Compressed Sensing,CS)框架下,可以通过多尺度压缩感知(基于数字信号)获取压缩表示形式[5-8],但这种模式还是基于传统的先高速采样、后大量丢弃的思路。人们开始考虑能否在执行模数转换时同时实现压缩,即直接获取压缩表示,然后完全重构其稀疏信息。
CS框架下的直接信息采样[9-11](Analog-to-Information Conversion,AIC)技术非常适合这些应用场景,已在机器学习[12]、图像压缩[13]、视频压缩[14]、无线传感器网络[15]以及模式识别[16]等等众多领域应用,能够大大降低数据采集速率(匹配信号的信息速率),因为AIC能够仅关注输入信号当中的信息,而这些信息往往是稀疏的。另外,有些信号尽管不是绝对稀疏的,但它们在像小波域这样的变换域中可压缩。国际上对AIC的研究取得了一些成果[9-10],它们往往假设信号在频域稀疏(存在有限个整数频率分量),对信号进行均匀低速的随机观测。这往往存在局限性,例如:采集对象为非多音信号的情况,均匀采样忽视了信号中不同的尺度在重构中占据的不同地位[17]。小波[18]在信号压缩中的优势不言而喻,现考虑建立多尺度直接信息采样框架,在采样的同时,针对信号的不同尺度,实行不同的观测速率即进行不同程度的压缩并重构。
1 自适应直接信息采样框架
1.1 AIC设计方案
直接信息采样系统由3部分组成:解调器、积分器以及常规采样单元,AIC设计方案如图1所示。模拟信号首先被一个NHz(信号x(t)的Nyquist频率)的伪随机最大长度PN序列pc(t)解调,其取值为±1,即
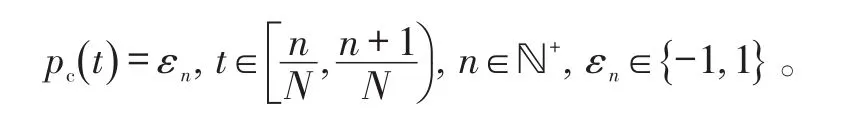
接着,对解调后的信号进行低通滤波,这里的低通滤波简化为一个积分过程,完成Ms时间内解调信号的累加。解调的目的在于扩展频谱以保证低通滤波后信息的完整性。最后,利用常规的ADC器件以速率M进行采样、量化后得到信息观测值序列y[m]。

图1 AIC设计方案Fig.1 Composition block diagram ofAIC
1.2 信号模型
信号x(t)在小波域稀疏或近似稀疏,将其在小波基上展开:

式(1)中:aj0,k为信号x()t的第j0级尺度系数;dj,k为信号x(t)的第j级小波系数。将信号x(t)的j级小波分解系数表示成矢量形式:
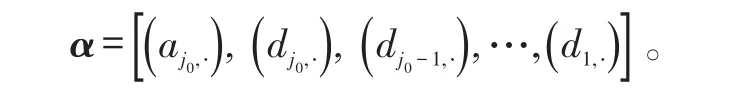
根据稀疏性假设,α中非零元素或大系数的个数应当远远小于系数的总数。
不妨在1 s内考察整个系统(当然也可以选择其他时间分辨率),现以离散时间表示信号,令

式中,T1=N为PN序列一个码元的持续时间,在这个时间间隔内PN序列取值为一个常数。因此,可以先来考察积分器对信号的作用:

这里,Φ(t)、Ψ(t)分别为尺度函数φ(t)、小波函数ψ(t)的原函数。
定义N×N矩阵:
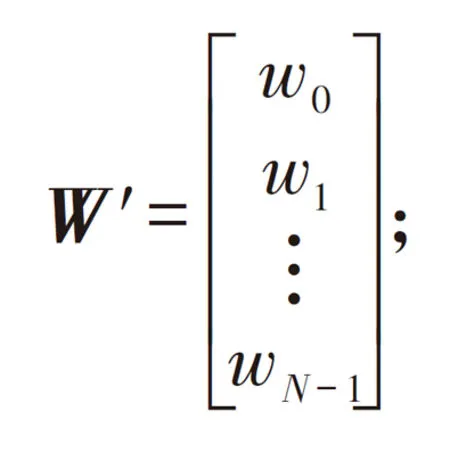


于是,式(2)可写为矩阵形式β=W′α。
1.3 自适应直接信息采样
因为PN序列一个码元的持续时间为T1=N,在1 s内PN序列的N个码元构成切割序列(Chipping Sequence)ε0,ε1,…,εN-1对信号的作用可写成矩阵形式β↦Dβ,其中,
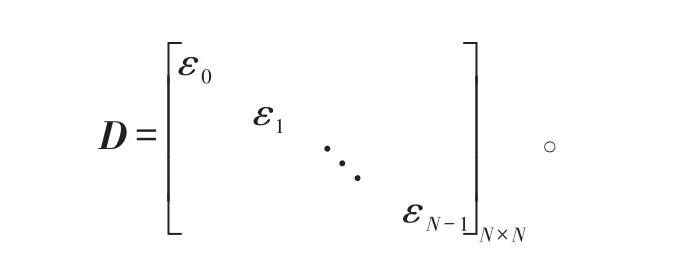
接下来考察低速采样器的影响。信号观测值可表示为:

当T1能够整除T2时(即M整除N),式(3)中的积分可以分解为个积分区间长度为T1的子积分,且在对应区间内pc(τ)为一个常数。低速采样器的作用可表示为一个M×N的矩阵H,其第i行从第列起为个连续的1,其余项均为0,i∈[0,M-1]。当T1不能整除T2时,则说明存在某些对观测值需要“共享”PN序列的一个码元。文献[11]中给出了一种近似:

由α的结构知道,其中尺度系数(aj0,⋅) 蕴含了大部分信号能量,考虑利用传统的Nyquist采样方式对其采集,而精细系数则用压缩采样的方式采集。
2 信号重构算法
矩阵W′的计算涉及第j0级尺度函数和第1至j0级小波函数的定积分,计算比较复杂,另外,现有算法往往基于均匀采样,因而在本文框架下实现自适应速率采样后性能将大幅下降。可考虑对W′进行简化。实现步骤如下:

式(6)中:H和G是分解低通和高通滤波器矩阵,分别由具有p消失矩的小波生成,它们的每一行都是一个长度为2j-1的矢量,如:
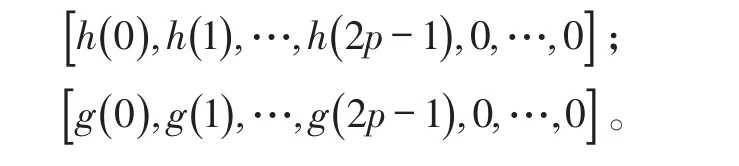
第i行则由其循环右移2( )i-1次;E为单位阵。
可以证明,这样构造的W是一个正交小波变换矩阵,而WT是逆变换矩阵。
定理1:令x为一个长度为N的信号矢量,X为其j-级正交小波变换,它们满足:

式(7)、(8)中:W满足式(5)、(6)定义,且WWT=E;X=[ajdj…d2d1]TN×1,其中,aj和dj为x的第j-级粗系数和精系数。
根据小波变换的定义:

且小波分解可用矩阵形式描述aj+1=Hj+1⋅aj,dj+1=Gj+1⋅aj。令



x=WTX。
恰如式(8),定理得证。
算法1:自适应正交匹配追踪(Adaptive Orthogonal Matching Pursuit,AOMP)。
AOMP(Φ,y)
Input:观测矩阵ΦM×N,观测值yM×1,正交小波矩阵WN×N,最大迭代次数m(稀疏度)
Output:目标信号估计x̂N×1

通过引入弱匹配因子μ,避免了常规贪婪算法需要稀疏度已知的难题,由迭代停止条件 ‖rn‖2>‖rn-1‖2可知,迭代过程中rn能量单调递减,算法至少收敛到一个局部最小点。
3 数值实验及结果分析
3.1 自适应直接信息采样重构实验
为了验证自适应直接信息采样和AOMP算法的有效性,使用长度为4 096点的测试信号作为Matlab/Simulink环境中的模拟输入。其Nyquist采样频率为8 kHz,原始信号如图2 a)所示。测量数M为1 024,选取sym3小波基,小波阈值ξ分别设置3个不同的值10-2、10和102以重构原始输入并对照。恢复信号的平均帧重构信噪比(Average Frame-Reconstruction SNR,AFSNR)为34.22dB、34.51dB和32.1dB,即,尽管信号仅通过Nyquist采样频率的25%进行测量,但绝大多数能量或信息包含在自适应直接信息采样的压缩观测数据当中。
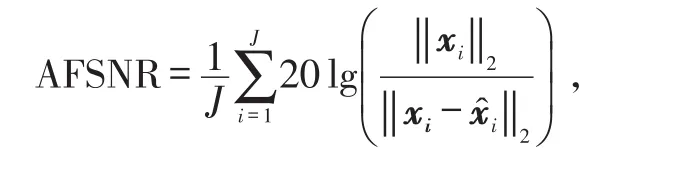
式中:J为总帧数;xi和x̂i为第i帧原信号及其重构信号。

图2 原信号以及3个阈值下的重构信号Fig.2 Original signal and reconstructed signal at three thresholds
3.2 压缩性能分析
对提出的多尺度自适应AIC系统和原始AIC系统的AFSNR性能进行了比较,采样率(M/N)范围为10%~100%。多尺度自适应AIC系统基于sym3和db2正交小波矩阵和AOMP重建算法,而原始AIC系统基于离散余弦变换(DCT)和OMP恢复算法。
从图3中可以看出,随着采样率的提高,AFSNR性能会越来越好。此外,发现多尺度自适应AIC系统具有比原始AIC系统更好的性能,并且sym3小波矩阵的AFSNR性能略好于db2小波。
3.3 分解级数对重构性能的影响
信号与前次实验相同,压缩比固定为25%,在多尺度自适应AIC系统中,基于sym3和db2正交小波矩阵和AOMP重建算法考察不同分解级数对重构性能的影响,考虑到信号长度,级数从1步进到10,结果如图4所示。
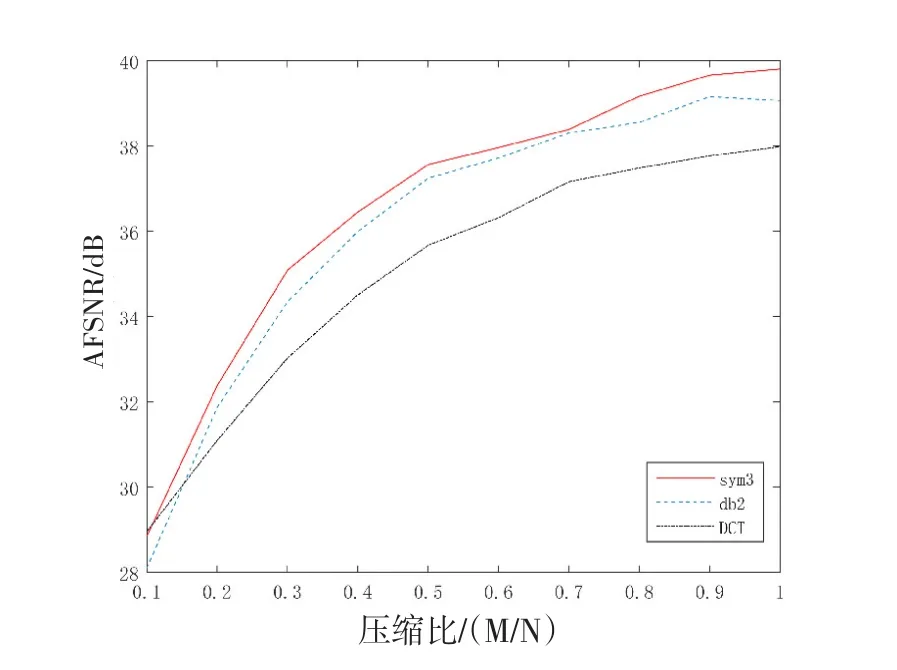
图3 压缩性能分析对比图Fig.3 Comparison of compression performance

图4 分解级数对重构性能的影响分析Fig.4 Influence analysis of decomposition level on reconstruction performance
图4表明,在分解级数较少的情况下(小于4),信号几乎不能重建,原因是其分解系数不够稀疏。此外,为达到相同的重构性能,sym3小波基下的重构要求的分解级数更少,而同样分解级数下,sym3小波基下的重构准确性比db2小波基下的重构准确性更好。
4 结论
本文提出了一种多尺度自适应直接信息采样与重构方法,通过在直接信息采样系统中引入自适应信息采样,实现对信号不同尺度的稀疏系数进行不同程度的压缩。该方法易实现,通过在恢复端引入小波矩阵等效地解决了信号压缩采集融合的问题。提出了自适应OMP算法,仿真结果表明,多尺度自适应AIC系统可以获得比传统AIC系统更好的AFSNR性能。
下一步可将多尺度自适应AIC系统推广使之适应不同的稀疏字典。

