舰载惯导传递对准仿真系统设计及实现
高继光,高青伟,吴 芳
(1.厦门大学,福建厦门361005;2.海军航空大学,山东烟台264001)
出于安全和成本等方面的考虑,传递对准误差模型和滤波算法的检验一般不可以直接到实际装备上,而且在实际装备中含有难以确定的随机误差,不利于算法的调试、分析和评价。一般首先在计算机上进行软件仿真,在此基础上进行半物理仿真,再到实际装备上验证。因此,计算机仿真是半实物仿真和实装验证的基础,即使有条件进行实际装备的试飞、试航试验,这个过程也是必须的。为了能够验证传递对准误差模型以及传递对准滤波器的可靠性,须进行不同战术条件下的多次试验。这将耗费大量的人力、物力以及时间,具有很大的难度,如果只进行有限的几次试验,又会使试验缺乏典型性和代表性。所以,设计计算机仿真系统,在试航试验前进行大量的计算机仿真试验,可以对试航试验提供有价值的指导。
1 计算机仿真系统的总体结构
在以往的计算机仿真中,大多通过解微分方程的方法利用模型产生量测值,这种仿真方法只能验证滤波方法是否有效,而无法说明所建立的数学模型是否反应系统的真实情况。
本文在文献[1-2]的基础上,设计了一种更符合实际情况的仿真系统进行仿真试验。整体结构如图1所示。
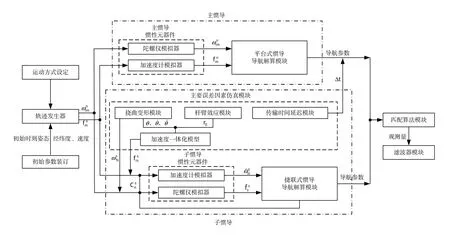
图1 惯导系统传递对准仿真结构图Fig.1 Fame chart of INS transfer alignment simulation
首先,设计轨迹发生器,对载体的运动进行仿真,让载体按照实际的运动规律或者战术要求机动;然后,设计了惯性器件模拟器,主要是根据主、子惯导系统的精度指标模拟主、子惯导加速度计和陀螺仪的理想输出;根据主要误差因素的数学模型,设计误差数据的仿真输出,将其与子惯导惯性元器件的理想输出叠加,产生子惯导系统的真实输出;接着,设计了惯性导航系统模拟器,利用惯性器件的输出,根据惯性导航原理,解算出载体的速度、位置和姿态等各种导航参数;根据选取的匹配算法模型,将主、子惯导系统的相应的导航参数匹配后输出;将匹配输出输入到选定的滤波器模型,验证模型的正确性和滤波的有效性。
2 轨迹发生器
轨迹发生器根据设定的运动参数:载舰所在的初始位置、航行速度、风浪情况、载舰的摇摆运动参数,为主惯导的惯性元器件提供输入信息[3]。
研究载舰在风浪中的摇摆特性,首先根据线形叠加原理,建立风浪与载舰摇摆之间的关系;然后,通过载舰载规则播种的试验或理论计算建立起来的船体要素和摇荡之间的关系,得到载舰在不规则波中的摇荡运动特性[4]。该运动可由一系列幅值和频率相近的正弦波来描述:
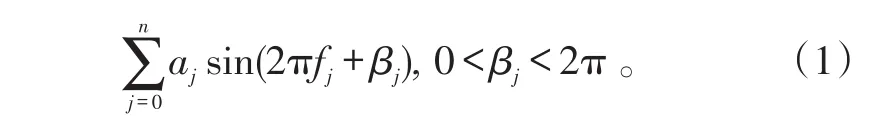
式(1)中:频率f的范围为 0.07~0.22Hz;幅值aj的范围为5~37mrad。
根据舰船摇摆的周期和幅值,在短时间内可以考虑载舰仅仅受到某一干扰频率和幅值的风浪而发生的自身的摇摆运动。
舰船三轴摇摆时,船体以正弦规律绕俯仰轴、横滚轴和方位轴摇摆,其模型为[5]:
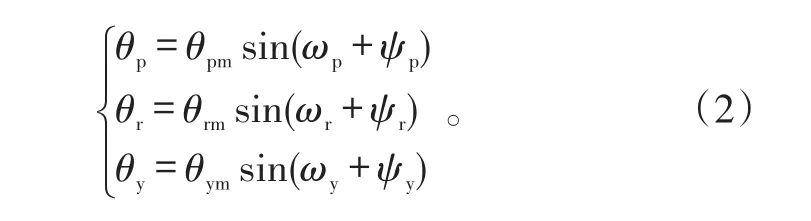
式(2)中:θp、θr和θy分别为绕俯仰轴和横滚轴的摇摆角度;θpm、θrm和θym分别为绕俯仰轴和横滚轴的摇摆角度幅值;ωp、ωr和ωy分别为绕俯仰轴和横滚轴摇摆的角频率,ψp、ψr和ψy分别为绕俯仰轴和横滚轴摇摆的初始相位。
另外,有ωi=2π/Ti,i=p,r,y,这里的Tp、Tr和Ty为绕俯仰轴和横滚轴的摇摆周期。可以根据不同的仿真环境,设置不同的初始相位和摇摆周期。
3 惯性元器件模拟器
运载体上安装的惯性元器件-陀螺仪和加速度计会感测到载体相对惯性空间的角速度和加速度。由于惯性器件在加工、安装等过程中不可避免地存在各种误差,使惯性元器件的输出中包含了各种误差因素。仿真中,主要考虑惯性元器件的安装误差和标度因子误差,以及陀螺仪的漂移和加速度的零位误差[6]。
根据舰载惯导系统传对准过程中的主要误差因素:挠曲变形与杆臂效应一体化加速度误差模型,挠曲变形角加速度模型和传递时间延迟误差模型,建立相应的仿真模块,运用Simulink仿真数据输出,输入到子惯导系统的惯性元器件输入端,模拟子惯导系统在考虑主要误差因素时的惯性元器件的测量输出[7]。

图2 杆臂效应和挠曲变形一体化加速度误差模型计算流程Fig.2 Computing flow of incorporate acceleration error model of lever-arm effect and flexure
4 惯导解算模块
惯性导航系统按惯性元器件的安装位置,可分为平台式惯性导航系统和捷联式惯性导航系统,相应的惯导解算也分为平台式惯导解算和捷联式惯导解算。本文所研究的传递对准技术中,主惯导系统可以为平台式或高精度的捷联惯导系统,子惯导系统为捷联式。
平台式惯导系统解算过程:轨迹发生器产生理想的线运动信息和角运动信息,根据主惯导的精度指标模拟产生主惯导的惯性元器件的输出,送入到惯导系统导航计算机,进行积分运算,得到各种导航参数。
捷联式惯导系统解算过程:在理想的线运动信息和角运动信息的基础上,考虑到子惯导所处的位置,结合一体化误差模型和子惯导的精度指标,产生子惯导系统的惯性元器件的输出,送入到子惯导系统导航计算机,计算机根据补偿后的测量信息解算出载体的航向、姿态、位置和位置等导航参数,在子惯导导航参数解算过程中,采用四元数法的归一化来实现解决捷联矩阵的正交化问题[8]。
5 匹配算法模块
根据舰载惯导系统传递对准中匹配算法模型,建立测量参数匹配模块和计算参数匹配算法模块以及不同的组合匹配算法模块[9-10],针对载舰在不同的环境和不同的机动方式下,研究不同的匹配算法对估计精度和时间的影响。
主要针对线形误差模型和非线性误差模型,采取组合匹配模型进行仿真验证,主要选取“速度+角速度”和“速度+姿态”2种组合匹配算法[11-13],如图3、4所示。对于主、子惯导系统传递对准的匹配算法,具体组合匹配算法的选取取决于主惯导系统是平台式惯导系统还是捷联式惯导系统,一般来所,如果主惯导系统是平台式,组合匹配算法采用“速度+姿态”,如果是捷联式,则2种组合匹配算法都可采用。
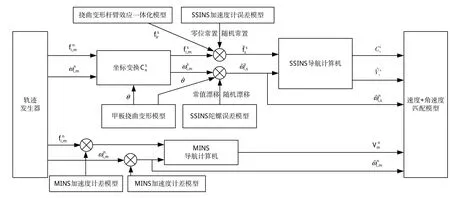
图3 “速度+角速度”匹配算法Fig.3 Matching algorithm of velocity+angle rate
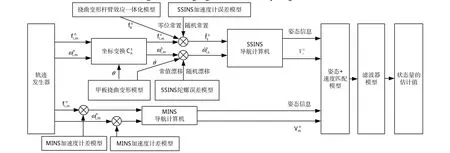
图4 “速度+姿态”匹配算法Fig.4 Matching algorithm of velocity+attitude
6 滤波模块
针对舰载惯导系统装配在不同位置的线性误差模型和非线性误差模型,根据所选定的匹配模型产生的观测量,送入相应的滤波模块,验证模型的正确性和滤波的有效性。采用的滤波模块主要分为2种:一种是针对线形误差模型,主要是采用kalman滤波器。同时,针对状态初始方差的不确定性,采用衰减记忆自适应kalman滤波器;针对多状态量估计的实时性问题,采用基于神经网络的kalman滤波器。另一类是针对非线性误差模型,主要采用非线性滤波技术—UKF滤波器[14-16]。同时,针对非线性滤波技术的实时性问题,采用单形采样UKF滤波器模型,提高对准时间。
7 系泊条件下大方位失准角线性模型传递对准仿真实现
本文仅选取系泊条件下舰载惯导系统大方位失准角线性模型传递对准过程进行仿真实现,传递对准滤波器模型的状态方程[7]:

式中,W=εs06×1η] 为系统白噪声。
利用状态方程可构造卡尔曼滤波方程。仿真条件[17]为:舰载在系泊情况下处于摇摆状态,横摇角幅值为12.5°,周期为12 s,纵摇角幅值为10°,周期为6 s,偏航角幅值为5°,周期为8 s。陀螺仪常值偏置为0.2(°)/h,加速度计零位偏置为3×10-4g。3个安装误差角为ϕax=20′,ϕay=40′,ϕaz=10′。舰载机机体坐标系与舰体坐标系之间的方位角为60°。二阶马尔可夫过程相关时间取τx=τy=τz=60 s[18],初始杆臂长度为[1 0 m 10m 5m]T。
“速度+角速度”组合匹配算法仿真。
观测量为:

式(4)中:H为观测矩阵;v为测量白噪声。
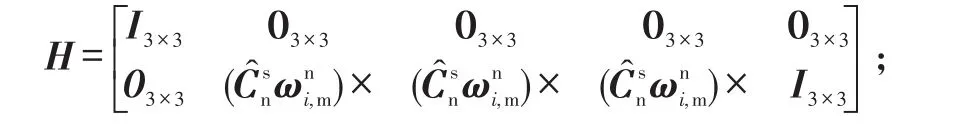
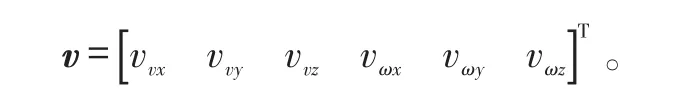
卡尔曼滤波器的初值选择如下:
X̂(0)=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]T。
初始方差阵P0为对角阵,其中:

图5、6分别为未补偿刚性杆臂加速度和补偿刚性杆臂加速度的安装失准角和挠曲变形角的估计误差曲线。从仿真曲线可以看出,采用“速度+角速率”组合匹配算法,未补偿刚性杆臂加速度时,安装失准角和挠曲变形角的估计误差曲线发散;补偿后两者的估计误差收敛时间和精度都高于未补偿时。
表1为2种仿真环境下安装失准角和挠曲变形角的估计误差。从表1可以看出,补偿刚性杆臂加速度前后的估计精度变化很大,未补偿时估计误差超过系统惯导系统的精度要求,补偿后安装失准角的估计误差最大为3.8′,挠曲变形角的估计误差最大为1.7′,在惯导系统精度范围之内,传递对准的准确性和快速性都满足惯导系统的精度要求。
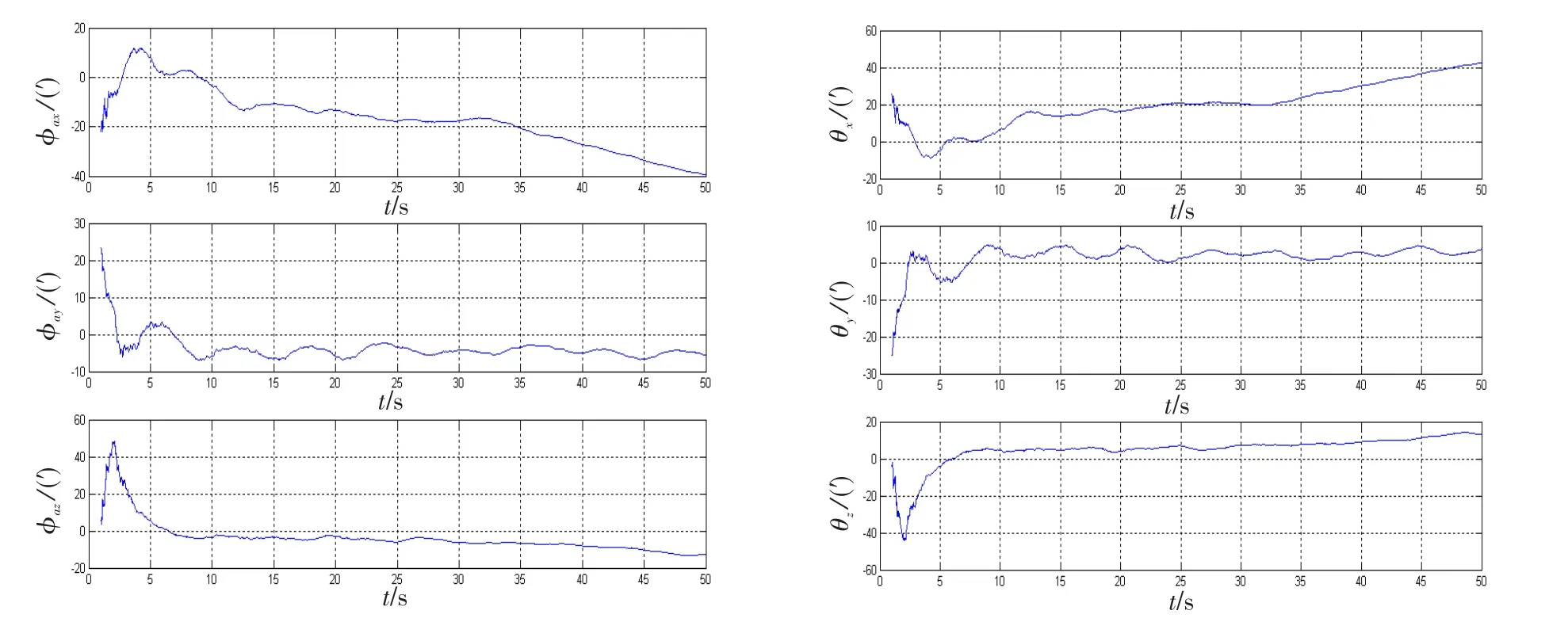
图5 未补偿刚性杆臂加速度安装失准角和挠曲变形角估计误差曲线Fig.5 Estimated error curve of fixed misalign and flexure angle with lever-arm uncompensated
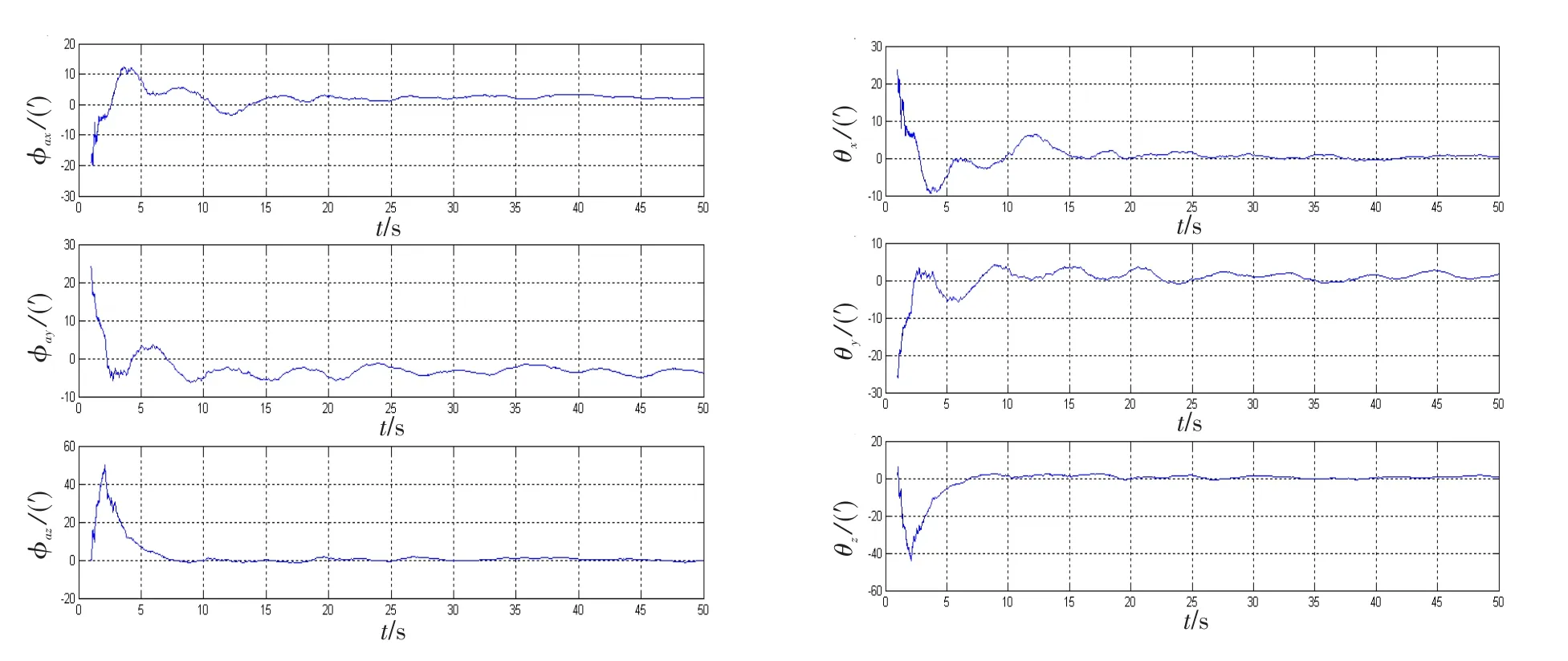
图6 补偿刚性杆臂加速度安装失准角挠曲变形角的估计误差曲线Fig.6 Estimated error curve of fixed misalign and flexure angle with lever-arm compensated

表1 2种仿真情况下固定失准角和挠曲变形角的估计误差Tab.1 Estimated error value of fixed misalign angle and flexure angle of two simulation conditions
8 总结
构建舰载惯导系统传递对准计算机仿真系统,可以有效验证所构建的惯导系统误差模型的正确与否和滤波算法的可靠性,并根据仿真结果对所建立的误差模型和滤波算法进行修改和完善,为下一步半实物仿真和实际装备的实验验证提供理论依据和支撑。

