有限域上一类特殊方程的解数估计
高 巍,张起帆
(四川大学数学学院,四川 成都 610064)
1 引言
对有限集合D 和正整数n ,用Dn表示D 的n 重笛卡尔积.对Dn的子集X ,用表示集合

2018 年李吉有在第五届川渝数论研讨会上指出下列看似简单的方程的计数问题也很困难.

为方便说明,我们引入记号,设D ={a1,a2,…,an} 是环R 上的有限子集,方程a1x1+a2x2+… +anxn=0满足xk∈D 且当j ≠k 时,xj≠xk的解的个数记为N(R,D) .
其中方程(4)与计算有限域上q -2 次置换多项式的个数本质上是一样的问题(见文献[4]).实际上方程(4)已经有很好的结果:Sergei Konyagin 和Francesco Pappalardi 在2002 年(见文献[5 -6])利用容斥原理以及指数和的计算,给出了方程(4)解数的一个很好的估计特别是在q =p 的情形,同年,Pinaki Das(见文献[7])利用矩阵的permanent 以及一个比较漂亮的代数方法构造了生成函数的方法也得到类似的估计本文我们将利用该方法解决关于的子群的问题:
在有限域Fp上,令正整数d |p -1 ,F∗p的d 阶子群μd={a1,a2,…ad} ,考虑方程=0 要求xk∈D 且当j ≠k 时,xj≠xk的解数问题.
对于一般性问题还是困难的,本文的主要研究结果是如下的:
定理1:在有限域Fp上,当p ≡3(mod4) 时,我们有

2 准备工作
为证明定理1,我们首先介绍一些定义:
定义2.1(见[8]):设A =(ajk)j,k=1,2,…,n是一个n 阶方阵,则定义A 的permanent 为
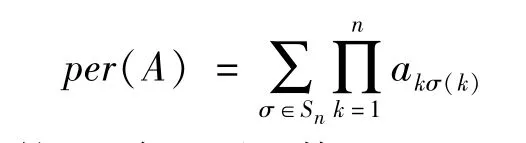
其中Sn是n 元对称群,σ 取遍Sn中的n!个n 元置换.
定义2.2:设A 是一个n 阶复方阵并且记AH是矩阵A 的共轭转置,矩阵AAH的特征值的平方根称为矩阵A的奇异值.
引理2.1:令A 是一个n 阶复矩阵,令α1,α2,…αn是矩阵A 的奇异值.则有

证明:参见文献[9 -12].
证明:由矩阵的permanent 定义,我们有

所以per(A) 中xm的系数cm是方程a1x1+a2x2+… +anxn=m 并且要求xk∈D 以及当j ≠k 时,的解的个数.当要求m ≡0(modp) 时,方程解数为
.则我们有

现在考虑1 ≤h≤p -1 的情况.
所以我们有:
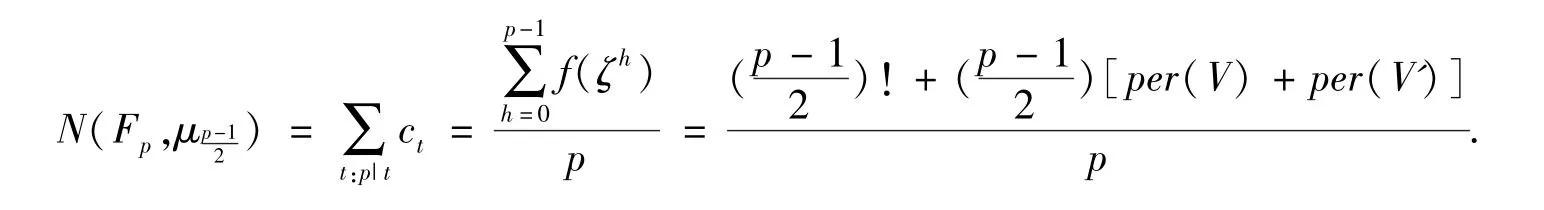
3 定理的证明
上一节我们已经得到了方程解数的表达式,当p ≡3(mod4) 时,我们有- 1 是模p 的非二次剩余(文献[13]),易知此时,所以本质上只需要计算per(V) 即可.下面我们根据引理2.1,利用矩阵V 的奇异值对per(V) 进行估计,即要计算VVH的特征值.
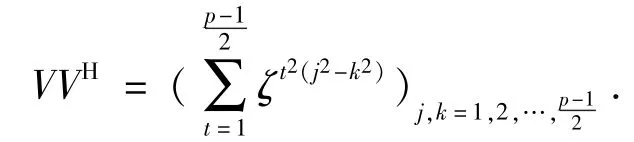
显然矩阵VVH是Hermite 矩阵,所以其特征值都是实数(见文献[14]),接下来我们将要分为三步估计VVH的特征值:
当p ≡3(mod4) 时,我们已经知道Gauss 和(文献[15])其中是Legendre 符号.并且.所以有
当p ≡3(mod4) 时,我们得到,当1≤m≤p -1 时其中是Legendre 符号.我们现在计算矩阵VVH第列的元素和:

所以矩阵VVH每列的元素之和均为从而是矩阵VVH的一个特征值.
第二步:证明矩阵VVH是半正定的:
所以矩阵VVH是半正定阵.
根据前两步我们已经知道矩阵VVH的特征值均为非负数,设矩阵VVH的特征值为
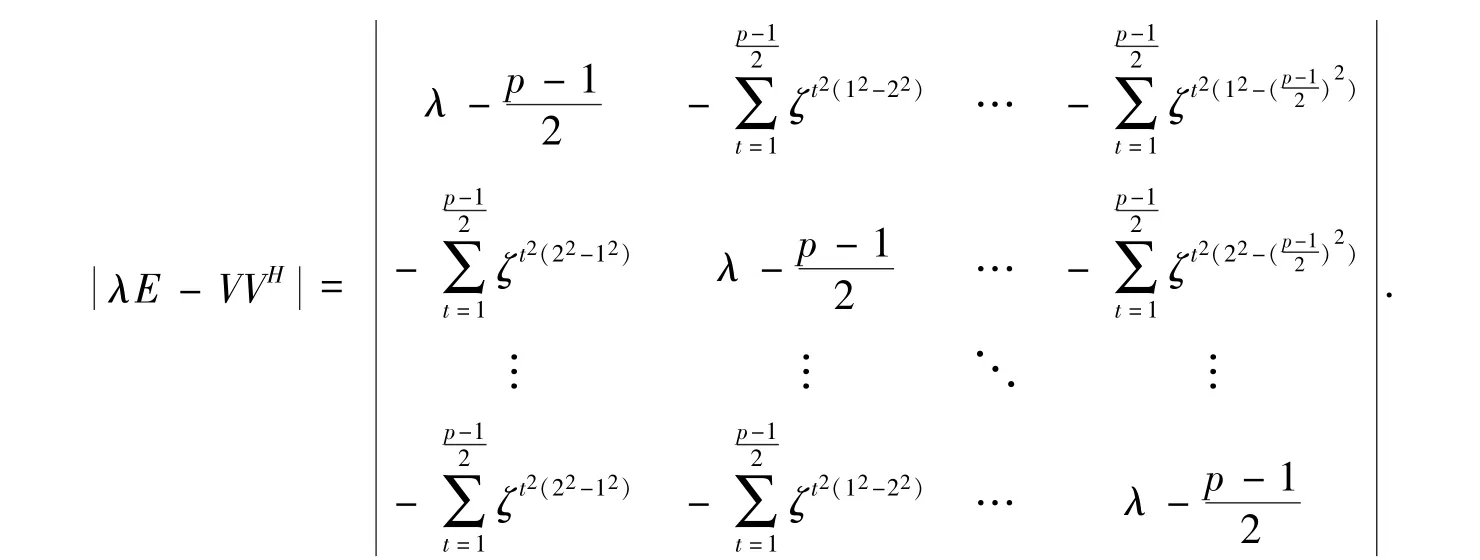
因在矩阵λE - VVH中每列的元素和均为,故有
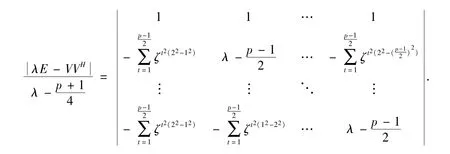
当j ≠k 时,
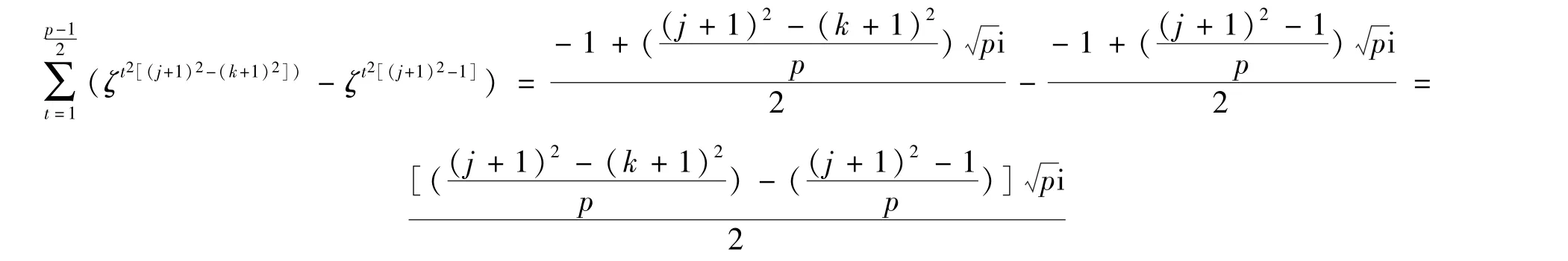
当j =k 时,

综上并结合引理2.1 可以得到per(V) 的一个估计:
由于当a,b ≥0 时,恒有an+bn≤(a +b)n,所以由引理2.1 我们有:

综上并结合引理2.3,我们得到定理1.

