弯曲河道对改善水生生物栖息地研究进展

张新华，邓 晴，文 萌，王 明

(四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065)

自然界中的河流大多蜿蜒曲折，河流的蜿蜒性使得河流能够形成干流、支流、河湾、沼泽、急流、缓流、浅滩和深潭等丰富多样的生境.天然河流中多样化栖息地有利于丰富生物群落的孕育. 例如浅滩生境中，由于光热条件优越，容易形成湿地供鸟类、底栖动物和昆虫栖息；深潭能够为不同鱼类提供繁衍场所，可以滋养多种大型植物与藻类群落，如图1 所示. 与顺直河道相比，弯曲河流的水流结构十分复杂，纵向流速和二次环流共同构成了弯道特有的螺旋流.螺旋流是弯道凹岸侵蚀和凸岸沉积的根本原因，对河流演变具有重要影响.若能充分利用弯道水流特征，尤其是利用其对河床形态的作用，就能创造多样的生境，丰富生物种类.由此可见，弯道水流具有明显的改善水生生物栖息地的潜质. 因此，正确认识河流弯曲度与河道生态环境的关系，研究其影响机制，对恢复河道生境有十分重要的理论价值和应用价值.

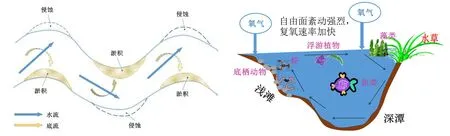
图1 弯曲河道环流及断面水生生物分布图Fig. 1 Helical flow and theaquatic organism distributions in a cross section of meandering rivers

近二十年以来，我国大范围尤其是西南地区大兴水利，修建了大量高坝，阻断了许多鱼类的洄游通道.加上河道渠化、河道硬化，严重破坏了河流生物的栖息环境，一些生物难以生存，这些负面影响已经严重威胁到了河道生态系统的稳定.尽管生态修复在理论和技术上己经取得了一定的成效，但河道生态结构修复在国内外还处于起步探索阶段，利用弯道独特水流结构改善水生生物栖息的研究报道较少，还未形成完整的弯曲河流栖息地修复理论体系. 为此，有必要系统梳理国内外弯道水流结构、泥沙运动、水生生物栖息地修复以及相关数值模拟等方面的研究成果，并对利用弯道水流进行生物栖息地修复的未来研究趋势进行展望.

1.弯道水流运动特性

河道内的水流结构与特性强烈地影响着水生生物的生存环境，在大量研究中，常将流速与水深作为对鱼类和底栖生物影响最大的水力要素，由此可知研究弯道内水流结构对开展栖息地修复研究有重要意义.

1.1 水面横比降

受弯道向心力的作用，天然弯曲河道中凹岸一侧水位增大，凸岸一侧水位下降，形成水面横比降.大量研究表明弯道横比降的最大值出现在弯道的弯顶或者弯顶以下，并向下游逐渐减小，弯道出口以后横比降逐渐消失. 在工程界中应用最广的是由罗索夫斯基[1]基于对数公式推导出的弯道横比降公式，但该公式在河床粗糙情况下存在计算值偏小的问题，针对此不足张红武、孙东坡、张海燕、刘焕芳、毛佩郁等[2－6]提出了不同的弯道横比降计算方法.王平义[7]基于凹凸两岸流速分布形式不同，分别提出了弯道凹岸区和凸岸区的水面横比降公式.

1.2 弯道环流

横向环流是天然弯道特殊水流结构的直接影响因素.流速向心加速度沿垂线分布的不均匀性使得表层水流趋于向外运动，底层水流趋于向内运动，在弯道断面上形成横向环流，并与纵向水流合成形成了螺旋流.1870 年，J.Thompson 在试验中最早发现了弯道螺旋流的存在，此后大量学者就这一独特的水力学现象开展了广泛的研究.罗索夫斯基[1]提出了与直段连接的单弯道的横向流动理论，张海燕[4]将罗索夫斯基的研究成果扩展到不规则连续弯道中，着重分析横向环流的产生和消亡过程.

弯道环流强度受多个影响因素作用，Pirestan[8]等人在U 型弯道物理模型试验研究发现环流的强度与弗劳德数的大小呈反比关系，当弗劳德数增加时，环流强度随之降低，反之亦然. 弯道断面形态对环流结构有直接影响，依据室内弯道水流试验和野外河弯实测资料显示，在凹岸陡坡截面上总是存在一对主体环流和一个反向次生环流，如图2 所示. 随着边坡坡度的变缓凹岸处反向次生环流变弱直至消失，而主体环流强度逐渐增大[9].当横断面为复式断面时情况有所不同，河漫滩区和主槽区内的环流强度存在此消彼长的关系，河漫滩区内的环流强度随着河漫滩范围的增大而增强，但主槽内的环流强度逐渐减弱.

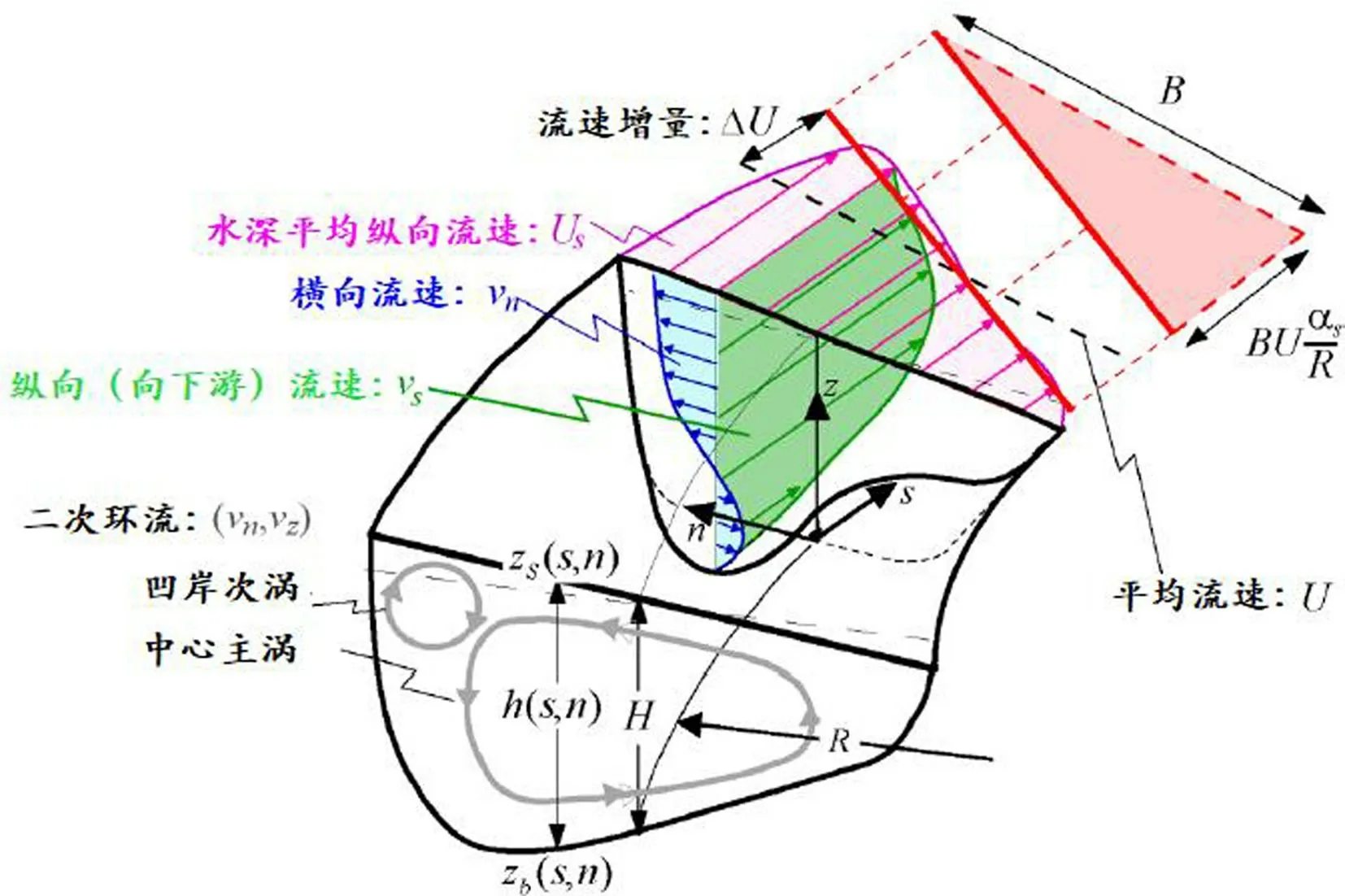
图2 弯道断面水流结构及主体环流和凹岸次生环流分布图Fig.2 Flow structure，main cell and concave secondary cell in a meandering channel

1.3 流速分布

弯道环流引起河道内水流结构重新分布，导致流速沿纵向、河宽和水深三个方向发生变化. 本节从断面环流流速分布和纵向流速沿程分布两个角度分析弯道水流流速分布的研究现状.

1.3.1 环流流速分布

据不完全统计，迄今为止国内外公开发表的明渠弯道恒定流的环流流速垂线公式多达15 个，这些公式具有各自的特征，多是基于椭圆型、抛物线型、对数型或者指数型垂线流速分布公式推导而来，但是对各个公式的可靠性、准确性及通用性没有统一的说法.

婴幼儿常患支气管肺炎,患病患儿年龄多为0.5—1岁[1]。咳嗽、肺部啰音以及气促是常见的临床症状。盐酸氨溴索联合布地奈德治疗小儿肺炎是常用方式,但依旧需要配合护理干预方式促使治疗效果提升[2]。因此,本文主要探讨盐酸氨溴索联合布地奈德治疗小儿肺炎的护理方式,为提升肺炎患儿护理质量提供合理的护理方式,详细报道如下。

在20 世纪30 年代早期，波达波夫[10]采用抛物线型流速分布公式推导出环流流速垂线分布形式，然而，在往后的研究并不认为它适用于时均紊流情况.1948 年，马卡维耶夫提出了基于椭圆型流速分布的最具代表性的环流公式，但是由于公式过于繁琐，难以在实际工程案例中使用.罗辛斯基及库兹明[11]、张耀先[12]、Odgaard[13]等人基于指数型纵向流速分布公式，推得环流流速分布公式，其中在变态模型罗辛斯基及库兹明公式中会得出环流沿水深的分布仍与原型相似的错误结论，张耀先的公式中无法反映河床粗糙度对环流的影响，而Odgaard 假设环流类似线性分布，这明显不符合实际. Engelund[14]针对二维宽浅矩形弯道，结合抛物线型流速公式提出了环流流速公式，这一公式为二次流的计算提供了新的思路，但是由于推导中一些不正确的假设，导致计算值偏小甚至会出现错误结果.还有许多学者根据概化弯道试验结果，从理论角度进行深入分析与总结，其中以张红武[15]提出的环流流速公式最具代表性，该公式能够较好的适应于不同粗糙度的河道中，在工程界运用最为广泛.

1.3.2 纵向流速分布

弯道纵向流速分布沿程都不断发生变化，水动力轴线在进入弯道之前就开始偏向凸岸，在弯顶断面几乎靠近凸岸边壁，自该点后又慢慢向河道中心线靠近，出弯后还继续向弯道凹岸偏转，经过一定距离才能恢复正常位置.1989 年王韦[16]对矩形断面人工弯道的纵向垂线平均流速进行了理论分析，提出了弯道内任一点纵向垂线平均流速的计算公式.1994 年，王平义[17]根据弯道水流在凸岸区纵向流速沿垂线服从对数分布，在凹岸遵循抛物线分布的规律，导出了分区域变曲率动床弯道水流纵向垂线平均流速计算公式，并从理论上对弯曲河道纵向垂线平均流速的横向与纵向变化规律进行了分析. 童思陈[18]利用弯道概化模型试验数据，从理论上推导了宽浅弯道纵向垂线平均流速沿程分布公式. 相较其他学者的研究成果，刘焕芳[19]提出的弯道纵向流速分布公式具有两大特色，一是该公式综合考虑了床面粗糙程度以及弯道形态要素如曲率半径、弯道中心角等对弯道纵向流速分布的影响，二是该公式能够反映不同区段的弯道纵向流速特点.

2 弯道泥沙运动特性

利用弯曲河道进行栖息地修复的实质是通过弯道水流对水沙结构的调整，创造多样化河床形态. 只有深入研究弯曲河道中泥沙的输移特性才能把握河流地貌空间异质性与水生生物多样性的响应机理.

曾庆华[20]曾对中心角为120°的矩形断面弯道水槽以及自然弯道的泥沙输移运动进行了详细的观测，得出底流轨迹与底沙运动轨迹并不重合，底沙是沿边滩向下游推移的结论.Hooke[21]利用弯道水槽测量数据得出，凸岸边滩形成的关键因素并非横向环流，而是由泥沙的横向与纵向输移运动导致的. 研究还表明，河道内推移质的运动强度与方向也会受到河床横向坡度的影响[22－24].

水沙特性研究的一个重要方向是泥沙颗粒的起动问题.泥沙颗粒的起动公式一般采用起动拖曳力、起动流速和起动功率这三种形式来表达.但由于起动拖曳力公式里面包含河底坡降项，然而坡降的量测在天然河道中较为繁琐且精度不高，因此在国内主要以起动流速公式研究泥沙起动问题为主. 众多学者[24－28]就研究泥沙起动问题，进行大量的野外调查收集了许多天然河道资料. 除了理论研究，学者们也开展了大量有关起动流速的试验研究，其中具有代表性的有Gilbert 与Kramer[29]、何之泰[30]、美国水道试验站(USWES)[31]、Meyer －Peter[32]、侯穆堂[33]、李保如[34]、窦国仁[35]等.另外，国内关于无粘性泥沙起动问题也取得较大突破，沙玉清[36]、张瑞瑾[37]、唐存本[38]、韩其为[39]以及窦国仁[40]等分别提出了不同的无粘性泥沙起动流速公式.

3 弯道水流及河床变形数值模拟研究

3.1 弯道水流数值模拟

基于垂向平均的平面二维数学模型在实际工程中应用较广，1976 年De Vriend[41]首次通过建立数学模型，对低雷诺数弱弯浅式河道水流进行了较为成功的模拟.1984 年，Moser[42]和Moin[43]对具有小曲率低雷诺数的弯道水流进行直接数值模拟，揭示了Taylor－Gortler 涡的存在. Leschziner 和Rodi[44]在1979 年成功模拟出180°天然弯道流动.这些模型由于未考虑弯道环流对纵向平均流速的影响，因此对于大曲率的宽浅河道的计算精度不高，针对这些缺陷，Lien[45]、易雨君[46]、魏文礼[47]等考虑环流影响的条件下建立了平面二维水流模型，对不规则弯道平面流场具有良好计算效果.

弯道水流在垂向上存在强烈的三维紊动特性，采用二维模型无法达到高精度 的要求，因此采用三维模型是未来深入研究的必然趋势.目前Simple 算法结合标准k － ε 模型模拟技术已经比较成熟，吴修广[48]、Shao[49]、许栋[50]、王博[51]等学者应用标准k －ε 湍流模型对弯道三维水流进行了模拟，得到了一些水流结构的三维特性.但标准k － ε 模型无法模拟湍流各向异性，对于强弯水流模拟存在失真，因此Spezi-ale、Thangam[52]对标准k － ε 模型进行了修正，建立了RNGk － ε 模型，并用其模拟了弯道分离流. 李琳琳[53]、Zhang[54]通过RNG 模型对连续弯道进行了三维模拟.胡旭跃[55]等引入VOF 方法对自由水面进行处理，结合RNG k－ε 湍流模型研究了过渡段长度与后弯水流稳定性的关系，具体成果如图3 所示. 李冰冻[56]等人采用RNG 模型结合VOF 模型研究弯道中心角对水流结构的影响，着重分析断面涡结构的变化，值得注意的是当弯道中心角增加时在弯道出口凸岸近水面会形成尺度较小的次生环流. 李艳红[57]等人将平面正交曲线坐标系和垂向σ 伸缩坐标系相结合建立三维水流数值模型，并采用嘉陵江典型横断面水位流速资料进行验证，模拟结果和实测数据吻合较好.

图3 过渡段回流范围变化Fig.3 Range of circulation length variation within a transition section

3.2 弯道泥沙运动数值模拟

国外的二维水流泥沙数学模型相较国内的发展历史更长，目前已有较为成熟的商业软件MIKE 21、TABS－2 、FAST2D 等，国内较有名的水沙模型有三峡的平面二维水流泥沙运动数学模型、黄河流域的平面二维水流泥沙运动数学模型.Nagata[58]假定泥沙颗粒全部沉积在床面上，建立二维非黏性河床变形数值模型.夏军强[59]等建立正交曲线坐标下的平面二维水沙数学模型，并将其应用于弯道水流运动、悬移质输移、河床冲淤变化计算中. 尽管平面水沙模型在实际工程中应用最广，但垂向水沙运动情况对进一步加深对三维水沙运动特性的理解至关重要，因此开展三维水沙数学模型研究是有必要的.

20 世纪70 年代开始，国外就已经着手三维水流泥沙模型的研究.Rijn[60]等人以对流扩散理论为基础建立了三维输运模型. 刘诚[61]等人在三维模型的研究过程中完善了对弯道曲线坐标系的调整和工程实际应用.Shimizu[62]在三维全沙动床数学模型中考虑悬移质输移对河床冲淤的贡献，使模型能够较好的模拟出由悬移质和推移质运动引起的弯曲河道河床变形.陆永军[63]建立的三维泥沙数值模型引入了湍流运动理论，对三峡工程坝区泥沙冲淤的模拟结果良好.

4 栖息地相关数值模型

随着计算机数值模拟技术的不断成熟，不少学者从20 世纪70 年代末开始对栖息地进行微观尺度的理论研究. Kemp[64]等提出以生态学定义的功能性栖息地和以水力学定义的水力栖息地的基本概念，使生态学和水力学紧密结合起来同时期，美国鱼类和生物服务调查中心构建和开发了可用于评价河道水生生物栖息地的河道内流量增加方法(Instream Flow In-cremental Methodology，IFIM)[65].该方法选择鱼类作为指示物种，以物理栖息地模拟为主，通过水动力模拟和指示物种对水动力要素的适宜性关系.2000 年以来，加拿大阿尔伯达大学以此为基础开发了二维栖息地模拟模型River 2D[66]，该模型可用于模拟小尺度生境单元内更详细的水力学过程以及生物栖息地的变化.目前，关于河道栖息地评价大多基于该模型.但是，该模型因缺乏泥沙和水质等模块，难以对一些规划或还未实施的生态修复措施对栖息地的改善效果做出及时的预测或评价.

根据保护生物学观点，保护生境是保护生物多样性最有效的方法. 因此，恢复或修复河道内水生生物栖息地的本质应该是创造更多可能的生境类型，以适应不同种类生物的栖息环境与条件.Kuhnle[67]等研究表明丁坝群作为常见的河岸保护建筑物，因为能创造并维持较为良好的栖息地条件，可运用于水生生物生境修复之中. Kang[68]等通过河工模型试验发现建立丁坝所形成的坝田区对于目标鱼种是适宜栖息地.吴瑞贤[69]等人基于HEC －RAS 和River 2D，以筏子溪河段作为研究对象，探究丁坝的坝高、坝长以及个数对为鱼类栖地的影响范围.范玥[70]等人利用River 2D分析在人工河道中丁坝间距的改变对平面流场以及栖息地适宜度指数的影响. 马冰等[71]以锦江成都河段为例，研究了双丁坝方案对栖息地加权可用面积的变化规律，且间距为4 倍坝长效果最好.李强等[72]基于IFIM 法，利用River 2D 模拟分析了成都市华阳河段不同的丁坝布置方式对栖息地WUA 的改善效果，得到的结论是丁坝可以改善城市河流水生生物栖息环境，且多丁坝布置方式下获得的栖息地加权可利用面积WUA 值最大. Shang － Shu Shih 等基于IFIM法[73]，研究了丁坝群对台湾地区特有鱼类—铲颌鱼、间吸鳅的栖息地可利用面积的影响. 研究结果表明，布置丁坝后，铲颌鱼、间吸鳅的WUA 值分别提高了404.8 –442.4% 、38.4 – 435.8%，并且目标鱼类WUA 值与Fr 值密切相关. Dongkyun 等[74]选择汉江内最主要的五种鱼类为研究对象，发现产生五种鱼类最大WUA 值时的流量约为某个鱼类最大WUA 值对应流量的两倍. 研究者还探讨了不同河床形态对WUA 值变化的影响，在首尔汉江中分别设置了砾石、丁坝和浅滩，结论是河道中布置浅滩时WUA 能达到最大值[75]，如图4 所示.

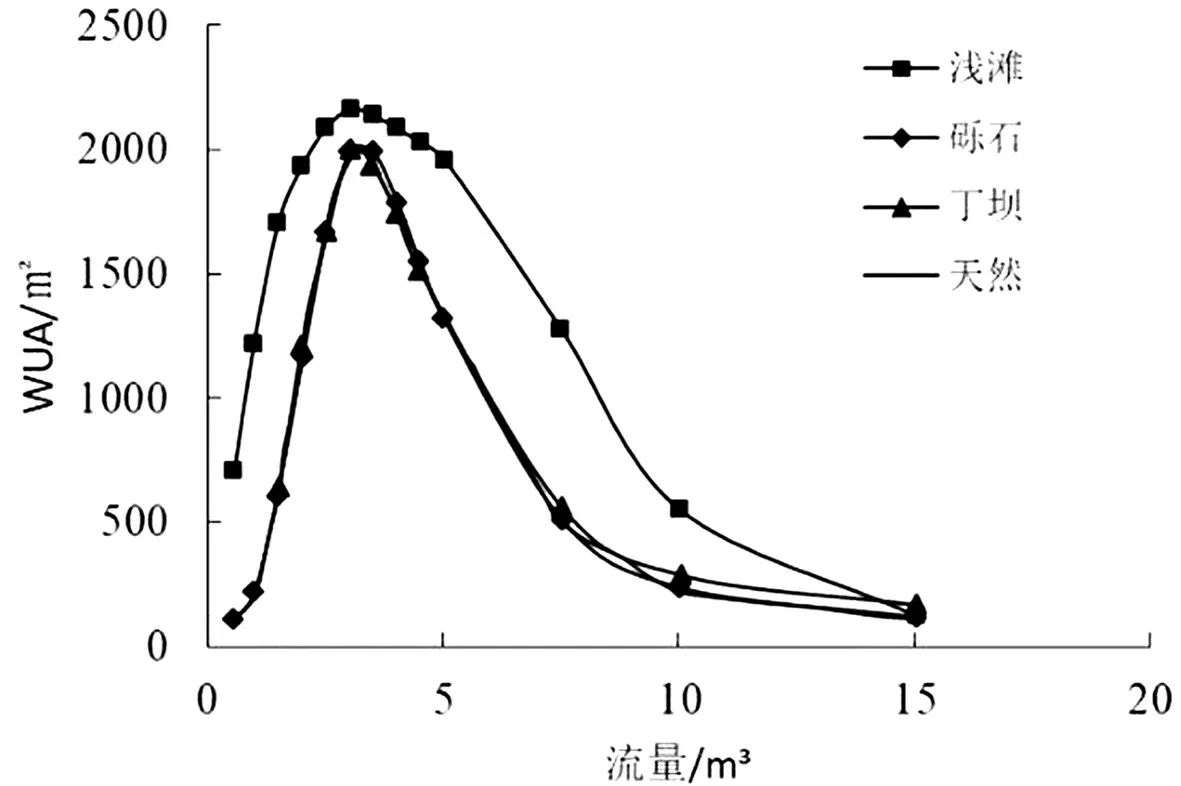
图4 不同流量下河床形态与WUA 的关系Fig. 4 Relationship between the river bed morphology and WUA at different flow discharges

目前，对河道栖息地有关的研究大多采用栖息地加权可利用面积WUA 来评价河道内水生生物栖息地环境与条件.但是，栖息地加权可利用面积WUA 值本身仅能反映栖息地的总量，忽略了栖息地的破碎程度和连通性，不能全面的描述栖息地或水生生物的生境质量.为了能揭示水生生物所需栖息地或生境的质量，Wang 等人基于图论中的最小生成树原理，在鱼类栖息地评价模型中引入生境连通性指数与栖息地破碎性指数[76]；Li 等人[77]基于景观生态学的连通性指数，对鱼类生境模型进行了改进；邵甜基于IFIM 法在栖息地评价模型中引入栖息地破碎性指数与连通性指数，对齐口裂腹鱼产卵场栖息地适应性与流量变化的关系进行了分析[78].可以看出，近年来不少学者认识到了单纯采用WUA 值不适宜评价栖息地质量，正尝试从更全面、客观的角度选取生境质量的评价指标与方法.

5 结论与展望

通过系统梳理国内外相关研究成果，关于弯曲河道及其对水生生物栖息地的影响研究虽然取得了较大进展，但是，仍存在一些问题需要进一步开展研究.从现阶段的主要研究成果来看，栖息地模拟中常采用二维水深平均水动力模型(以River 2D 为代表)，忽略了水沙耦合、河床形态演变作用对生境质量的影响，同时，也大多未考虑水质的变化，并且对一些底栖鱼类和一般底栖生物而言，河床附近水力要素对其生殖繁衍具有重要影响，二维水深平均水流模型无法揭示河床附近水力特征. 另外，目前关于栖息地的评判方法并不统一，存在很大的不确定性与不准确性，如水生生物对水力学与栖息地参数的适宜性指数HSI受选择物种的生活习性、不同生长阶段及调查时间、次数等众多因素影响；再有，选取的表征生物栖息地修复效果的指标也相对单一，尚未全面系统地开展弯曲河道与水生生物栖息地修复关系的定量研究.

针对上述不足，未来关于利用弯道改善水生生物生境质量可以从以下几个方面开展进一步研究:

(1)结合生态水力学，对弯道三维水沙特性、河床形态以及物质输移特性进行精细化研究，从微观尺度上探讨河流弯曲度与水生生物栖息地多样性之间的作用机理.重点探索三维水沙耦合作用下对生物栖息地质量的影响机理以及河流地貌异质性与水生生物多样性的响应关系，分析弯曲河道地貌空间异质性的水生态意义.

(2)水生生物栖息地适宜性指数HSI 方面. 栖息地适宜性指数考虑了水生生物对物理生境的要求，栖息地质量评价内容中的重点是定量化水生生物对栖息地的偏好与栖息地生境之间的关系.目前主要考虑的评价因素多为水动力方面的水深、流速和河床基质与选择的单一指示物种如鱼类或底栖类之间的偏好关系，要准确地建立这些关系非常困难，因受众多因素影响或干扰，如鱼类栖息场所并不固定，不同生长阶段的生活习性和喜好也不尽相同，调查时间不同，结果也可能迥异. 如何排除这些影响及其不确定，是否存在既能综合水动力、水质、泥沙影响，又能反映水生生物偏好的指标与评价方法? 这些都还有待进一步去探索.

(3)河道弯曲度与生物多样性的相关关系. 在栖息地评价体系上，除关注水动力因素，还应涵盖水生生物生物量、丰富度、均匀性、栖息地破碎化、栖息地连通性、水质状况、食物链等多项内容，综合考虑作为衡量生境优劣的指标，建立更完善的栖息地质量评价模型.

(4)为维持河道生态系统功能的稳定性与整体性，应从流域角度综合考虑. 不拘泥于微观尺度栖息地数值模拟研究，进一步开展栖息地保护与恢复在不同尺度与不同空间格局需求等方面的研究，探寻有利于生物多样性增长与保护的适宜河道弯曲度范围、数量及其在流域尺度上的分布规律等.