质子衍射的束缚态理论研究

刘以良，滑亚文，孙翼飞

(西南民族大学电气信息工程学院，四川 成都 610041)

当今，建立在实物粒子波动性基础上的理论研究得到长足的发展，电子衍射技术继而成为研究材料内部微观结构的重要手段[1－2].尤其是近年来，作为一种有效的分子结构诊断和跟踪手段，分子的超快电子衍射实验受到了广泛的关注.例如，He 等通过在氦滴中增加分子浓度的方法加强衍射的效果，得到了CBr4分子的电子衍射图样[3].Stefanou(史蒂芬)等人的量子分子动力学研究也发现X 射线和超快电子被光激发的乙烯衍射后具有相似的衍射信号[4].

然而，一方面，分子衍射图样分辨率较低，并且气相分子的取向排列具有随机性，衍射图样只能得到一维信息，并且距离相差不大的原子在电子衍射图样下难以分辨.尽管Hensley(汉斯莱)以及Yang 等甚至通过记录排列的气相分子的电子衍射图样构建出CF3I 和N2等气相分子的三维图像[5－6]，但是鉴于单分子在强电子束辐射下极易遭到破坏，真正意义上的单分子电子衍射实验目前还难以实现.另一方面，研究人员通常以物质波理论为基础[7]，多关注衍射图样与分子结构的关系，对于衍射条纹上明暗相间的特性的本质却少有关注.

毋庸置疑，当今的量子力学理论基本都得到了实验的证实，人们对其应用也没有什么怀疑.然而，对于量子力学的正统理论仍然有人提出不同的意见，称其为“来自北方的迷雾”[8].例如，关于量子纠缠、薛定谔猫态以及微观粒子波动性等还有很多令科学家困惑的问题[9–11]，费曼提出电子的双缝干涉实验是量子力学的核心问题，近年来，科学家试图测量电子双缝干涉实验中衍射电子的运动路径.然而一旦产生测量行为，干涉条纹即消失.Copenhagen(哥本哈根)认为是测量仪器的干扰导致干涉条纹的消失. Rempe(伦珀)等利用一束冷原子对光驻波的衍射做了测量路径的实验，他们用原子的内部态标记原子束的路径，衍射条纹同样消失[12].Rempe(伦珀)和Knight(克耐特)认为应该用粒子间的量子纠缠来解释干涉条纹的消失[12－13].

本研究中，我们提出质子通过极窄的狭缝时处于束缚态，在纵向分布必然是量子化的，我们称之为瞄准距离的量子化.因此，相应的散射方向也应该是量子化的，即:屏幕上势必会出现明暗相间的条纹.鉴于以上假设，我们以单个质子通过两个原子核间的模型为研究对象，通过量子力学方法计算量子化的瞄准距离，结合经典力学方法研究质子衍射运动轨迹，并与夫琅禾费单缝衍射公式bsin(θ) ＝kλ 进行比较.

1 计算方法

我们以质子被两个相距b ＝2.88 ×10－8cm ，原子序数Z ＝79 的Au 原子核衍射为模型，以两个原子核的中心为坐标原点，以两个原子核的连线为y 轴.为了得到衍射过程中单个质子经过两个原子核之间时量子化的瞄准距离，我们假设质子束缚于两个原子核之间的连线上，根据定态薛定谔方程可以求解概率密度的极大值.

势能方面，考虑单个质子与两个原子核的相互作用势能函数，则质子受到的库仑势能为:

其对应的势函数如图1 所示:

图1 质子在两个原子核间的连线上运动时的势能Fig. 1 Potential energy of the proton between the nuclei.

定态薛定谔方程为:

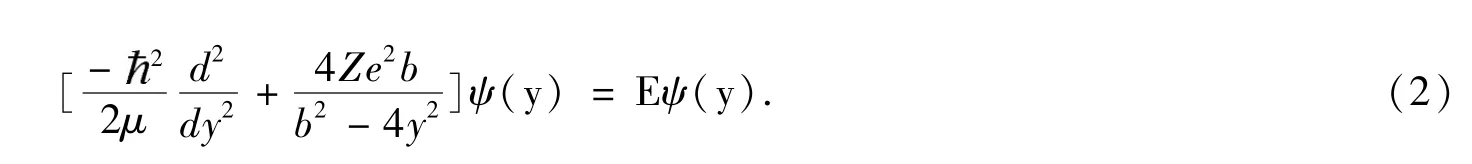
这是一个变系数二阶常微分方程，为了得到这个方程的近似解，我们求解原点附近方程的解，即:

则(2)式变为:

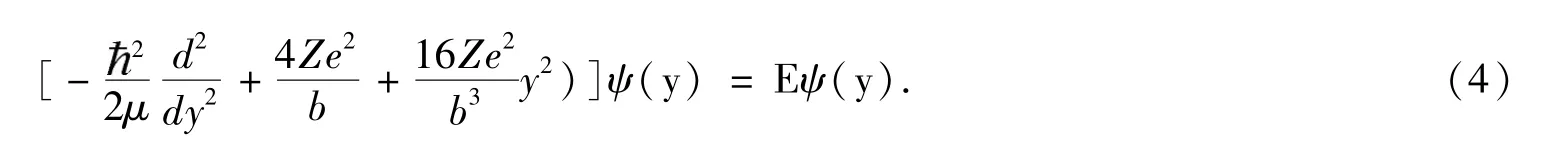
则:

则:

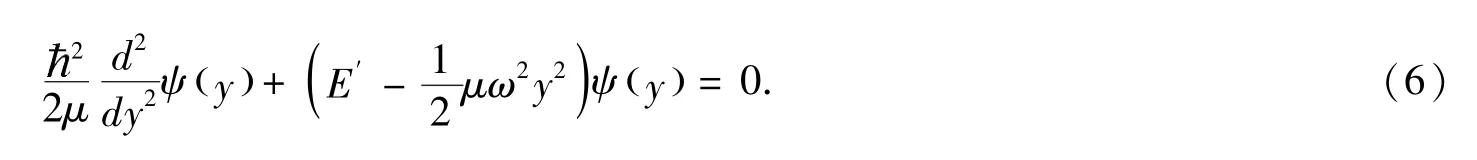
上式是一维线性谐振子的本征值方程，其归一化的本征函数为:

其对应的基态、第一激发态以及第二激发态波函数分别为:

对应的概率密度为:

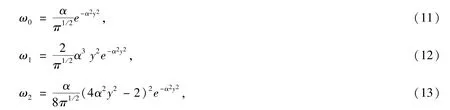
基态以及第一和第二激发态的概率密度如图2 所示:

图2 基态以及第一和第二激发的概率密度Fig. 2 Probability densities of the ground state，first excited state and second excited state

根据下式:

基态、第一和第二激发态的概率密度对应的极大值的位置:

此外，质子在xoy 平面内在不同位置的库仑势为:

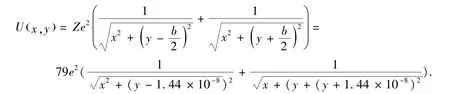
则衍射过程中质子在x 方向和y 方向的受力分别为:

2 结果与讨论

分别选取y1＝±4.06 ×10－10cm 和y2＝±6.42 ×10－10cm 作为量子化的瞄准距离，以经典力学方法为基础，参考分子动力学计算方法，计算单个质子沿x 轴方向入射后在力场中的运动轨迹.其中，动能方面，考虑分别用50eV，100eV，200eV，300eV，400eV，500eV 的电压加速质子，动力学模拟的时间步长设置为t ＝1.0 ×10－24s.

表1 质子单缝衍射一级明纹衍射角的正弦值Table 1 Sine of angle for the first diffraction maximum in the single－slit diffraction of protons

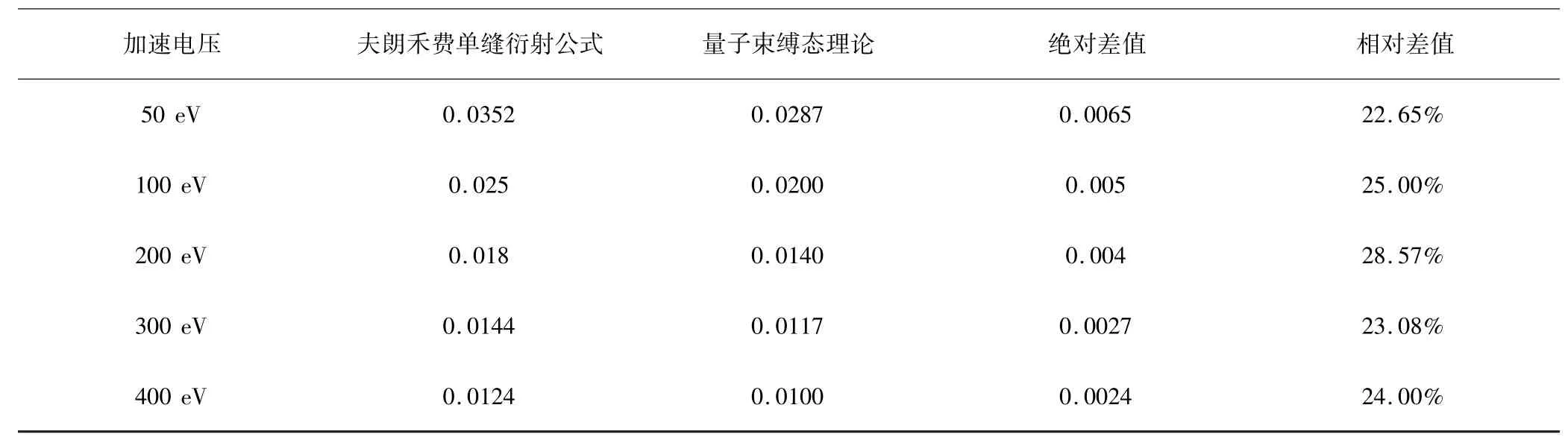
表2 质子单缝衍射二级明纹衍射角的正弦值Table 2 Sine of angle for the second diffraction maximum in the single－slit diffraction of protons

3 结论

电子的双缝衍射实验被认为是量子力学的核心问题，德布罗意假设认为微观粒子具有波粒二象性，结合惠更斯－菲涅尔原理，物质波理论可以解释微观粒子的衍射现象.本文中我们提出可以利用量子力学束缚态理论解释微观粒子的衍射现象.根据束缚态理论，质子经过双原子核之间时，其波函数的空间分布必然是量子化的，我们称之为瞄准距离的量子化.结合经典力学理论，质子衍射图样势必会出现明暗相间的条纹.

研究发现通过量子力学束缚态理论，粒子性同样可以解释微观粒子的衍射现象，并且与微观粒子的波动性解释吻合的较好.尽管波动性和粒子性仍然存在20%左右的相对误差，我们认为这是由于，一方面，在计算过程中我们对势函数进行了原点附近的近似求解.另一方面，质子从两Au 原子之间穿过时，只考虑了质子与带正电的原子核之间的作用，没有考虑质子与原子核外围电子之间的相互作用.

本研究为波动性和粒子性提供了一个枢纽，为以后更深层次地研究波粒二向性提供了一种思路.