锥b－度量空间中广义Boyd－Wong 压缩映射的不动点

彭 荣

(广东培正学院数据科学与计算机学院，广东 广州 510830)

不动点定理是解决非线性问题的重要工具，在各个数学分支中应用非常广泛.1922 年，Banach 提出了压缩映射原理.随后，压缩映射原理受到了学者们的广泛关注和研究，得到了各种形式的推广. 1998 年，Czerwik 在文献[1]中提出了b 度量空间的概念，推广了度量空间中的一些不动点定理[2－5]. 2008 年，Huang and Zhang 在文献[6]中用Banach 空间代替实数，提出了锥度量空间的概念，并证明了锥度量空间中的不动点存在和唯一性问题，推广了许多不动点结论[7－11].2011 年，Hussain 和Shah 在文[12]中提出了锥b－度量空间的概念，推广了锥度量空间和b－度量空间中的一些结论，获得了锥b －度量空间中压缩和非扩张映射的不动点定理[13－16]. 本文在锥b －度量空间中，运用偏序关系和迭代法，讨论了一类广义Boyd－Wong 压缩映射的不动点存在唯一性问题，获得了几个不动点定理，推广了一些Boyd－Wong 压缩映射及凸收缩映射的相关结果，并改进了证明方法.

1 预备知识

为了后面阐述方便，下面介绍一些相关的概念与基本结论.

定义1 设E 为实Banach 空间，θ 表示E 中的零元，集P 为E 的一个子集，如果集合P 满足:

(i) P 非空闭集且P ≠{θ} ；

(ii) ∀a，b ∈R∗，x，y ∈P ，则ax ＋by ∈P ；

(iii)若x ∈P ，－ x ∈P ，则x ＝θ ；

定义2 设X 为一个非空集合，E 是实Banach 空间，向量函数d:X × X →E ，满足:

(ii)对任意x，y ∈X ，d(x，y) ＝d(y，x) ，

性质1 设(X，d) 为锥b－度量空间，则

(i)若序列{xn} 收敛，则xn的极限唯一；

(ii)若序列{xn} 收敛序列则xn必为Cauchy 序列.

性质2 映射φ:X →X 满足条件

(i) φ 单调增，

(ii) φ(x) ＝θ⇔x ＝θ 且对任意r ≻θ 都有φ(r) ≺r ，

定义5 设(X，d) 是一个锥b－度量空间，s 为系数，映射T:X →X ，如果满足

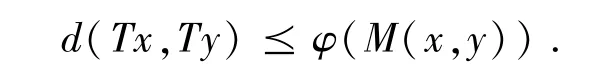
其中M(x，y) ＝max{d(x，y)，d(T(x)，T(y))，…，d(Tm－1(x)，Tm－1(y)) ，则称映射T 满足广义Boyd －Wong 压缩条件.

性质3 设(X，d) 是一个锥b－度量空间，s 为系数，则对任意p，i ∈N 和x0，x1，x2，…，xp∈X ，都有

证明:任取p ∈N ，xi∈X 则

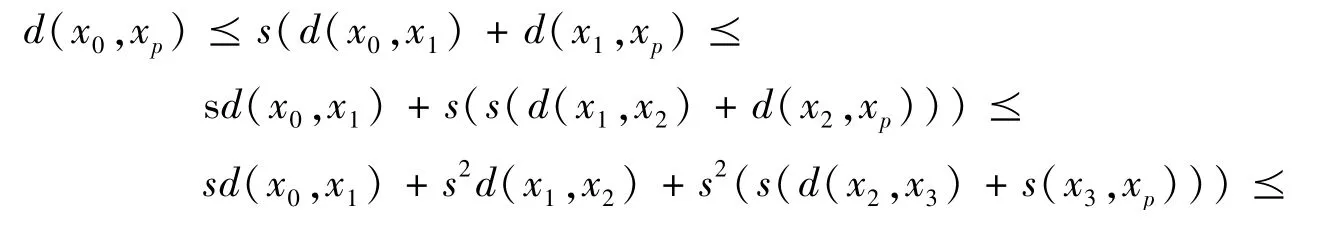
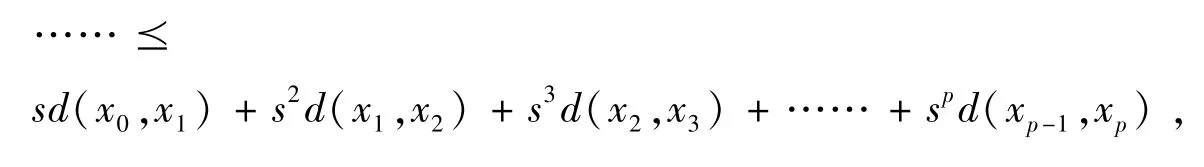
2 主要结果

定理1 设(X，d) 为完备锥b－度量空间，系数s ≥1 ，P 为X 上的锥，T 是X 到X 的连续映射，如果存在m∈ℕ ，对任意x，y ∈X 满足广义Boyd－Wong 压缩条件，即

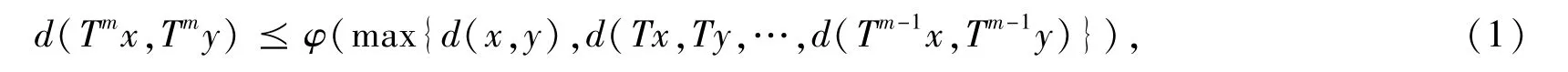
则T 在X 中存在唯一的不动点.

证明:任取x，y ∈X 且n ∈ℕ ， 记xn: ＝Tn(x) ，yn: ＝Tn(y) ，记

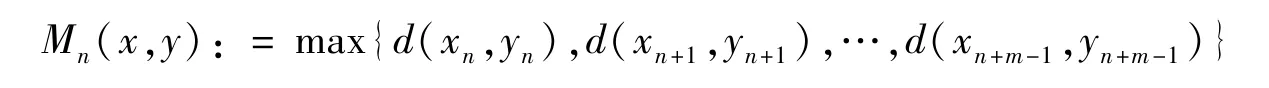
命题1 序列{Mn(x，y)} 单调递减

事实上，取x ＝xn，y ＝yn代入(1)式中，则

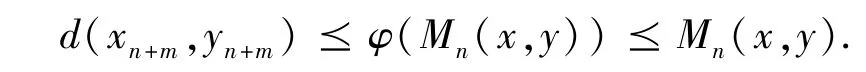
因为Mn＋1(x，y): ＝，所以

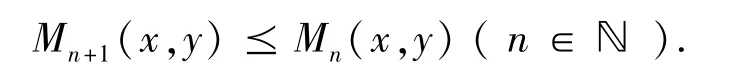
即序列{Mn(x，y)} 单调递减.

事实上，由命题1 知序列{Mn(x，y)} 单调减，且Mn(x，y) ⪰θ. 任取n ∈ℕ i ∈{0，1，2，3，…，(m －1)} ，取x: ＝xn＋i，y: ＝yn＋i代入(1)式，则

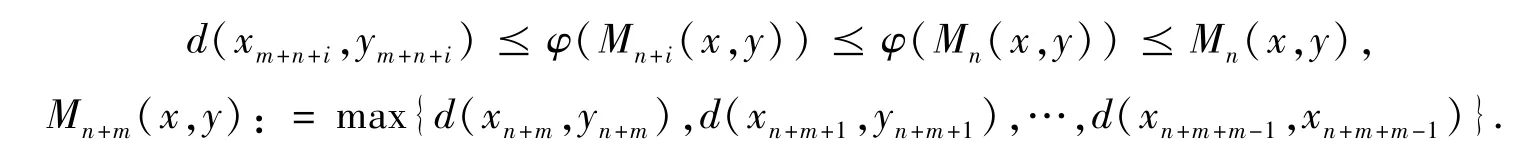
由数学归纳法可以证明Mn＋km≤φk(Mn(x，y)) . 事实上，当k ＝1 时，结论显然成立. 假设对n ＝k 时结论成立，即Mn＋km≤φk(Mn(x，y)) .则当n ＝k ＋1 时，

令x ＝xn＋km＋i，y ＝yn＋km＋i，其中i ＝0，1，2，…，m －1 ，代入(1)式得

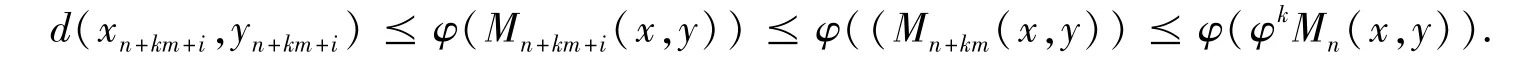
Mn＋(k＋1)m(x，y): ＝max{d(xn＋km，yn＋km)，d(xn＋km＋1，yn＋km＋1)，…，d(xn＋km＋m－1，yn＋km＋m－1)} 因此，Mn＋(k＋1)m(x，y)

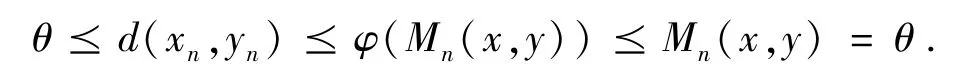
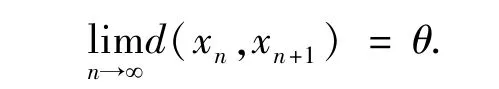
命题3 序列{xn} 为cauchy 序列

(i) d(xmk，xnk) ⪰ε0，其中

(ii) d(xmk－1，xnk) ≺ε0.

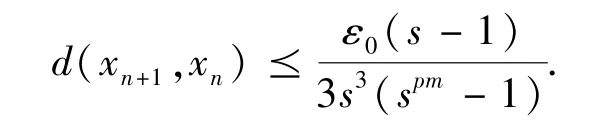
取C: ＝(s3＋1)ε0，则当mk> nk> n′＝max{n0，n1} 时，有

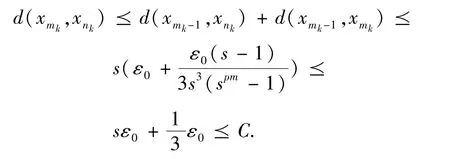
当i ∈{1，2，3，…，m －1} 时，有

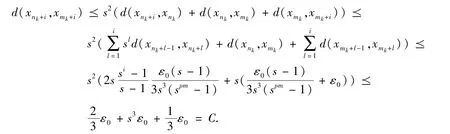
又因为M0(xnk，xmk) ＝max{d(xnk，xmk)，d(xnk＋1，xmk＋1)…d(xnk＋m－1，xmk＋m－1)} ，则

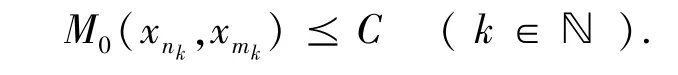
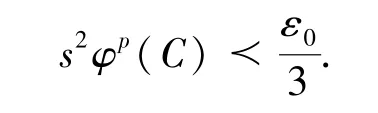
综上，对于k ∈N ，当nk≥nε1时，由

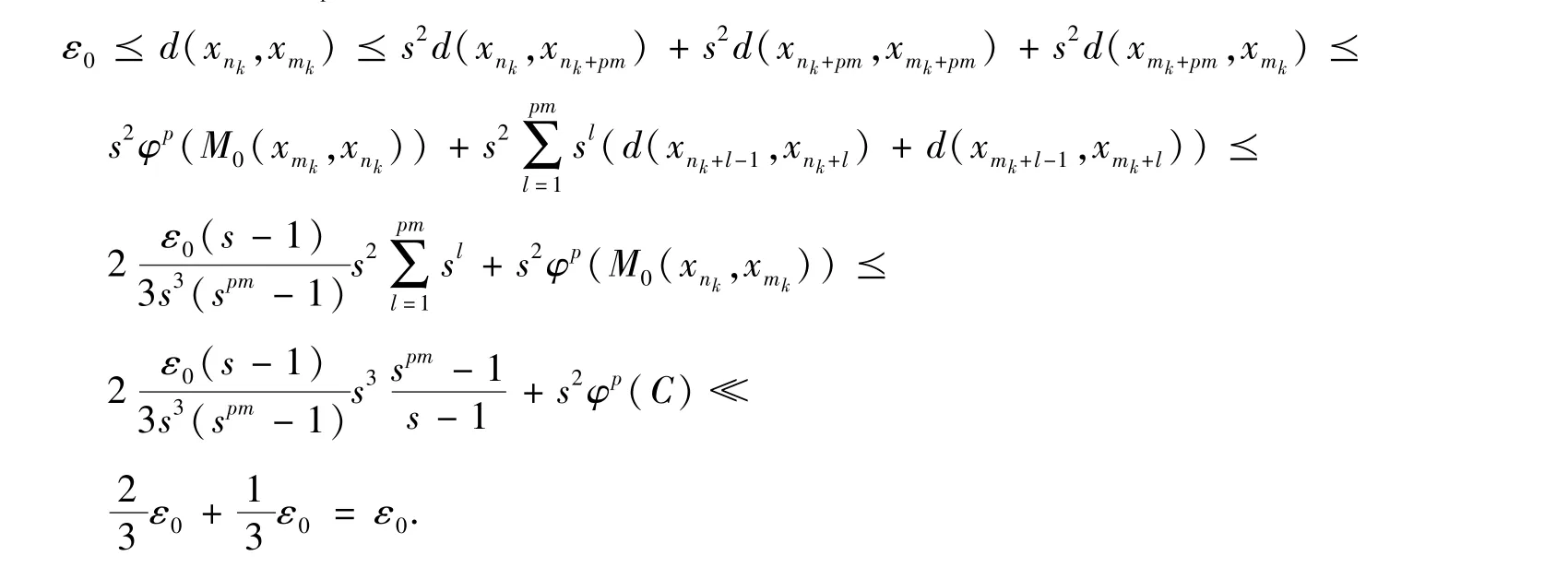
显然矛盾，由反证法可知 { xn}为cauchy 序列.

由于(X，d) 为完备锥b－度量空间，则存在x′∈X ，使得又由T 的连续性可知

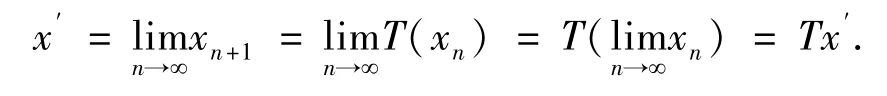
即x′是映射T 的不动点.

T 的不动点是唯一的.事实上，假设x 不是唯一不动点，即存在x∗≠x′，也满足T(x∗) ＝x∗，代入(1)式，则

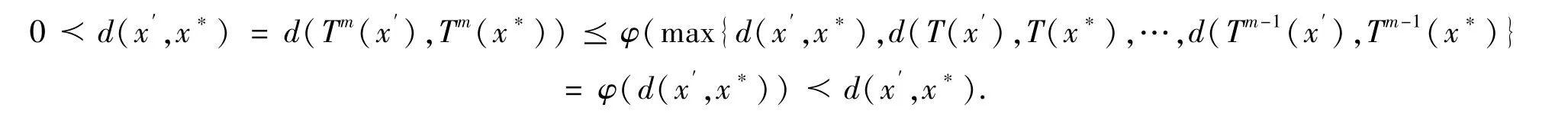
显然，矛盾. 因此假设不成立，即T 在X 中有唯一不动点.

推论1 设(X，d) 是一个完备锥b－度量空间，系数s ≥1 ，P 为X 上的锥，T 是X 到X 的连续映射，满足Boyd－Wong 压缩条件，即存在m ∈ℕ ，对任意x，y ∈X ，

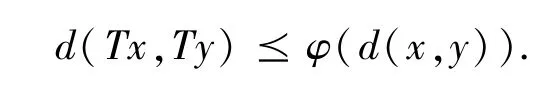
则T 在X 中有唯一不动点.

证明:令m ＝1 ，则M(x，y) ＝d(x，y) ， 类似定理1 证明即可.

推论2 设(X，d) 是一个完备锥b－度量空间，系数s ≥1 ，P 为X 上的锥，映射T:X →X 连续，且存在m ∈N ，k ∈[0，1) ，使得:

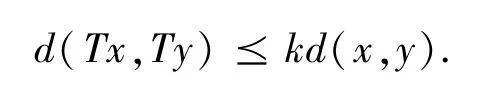
则映射T 在X 中存在唯一的不动点.

证明:由推论1，令φ(t) ＝kt

推论3 设(X，d) 是一个完备锥b－度量空间，系数s ≥1 ，P 为X 上的锥，T 是X 到X 的连续映射，且存在，使得:

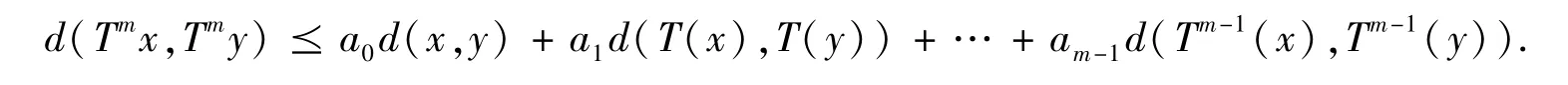
则映射T 在X 中存在唯一的不动点.

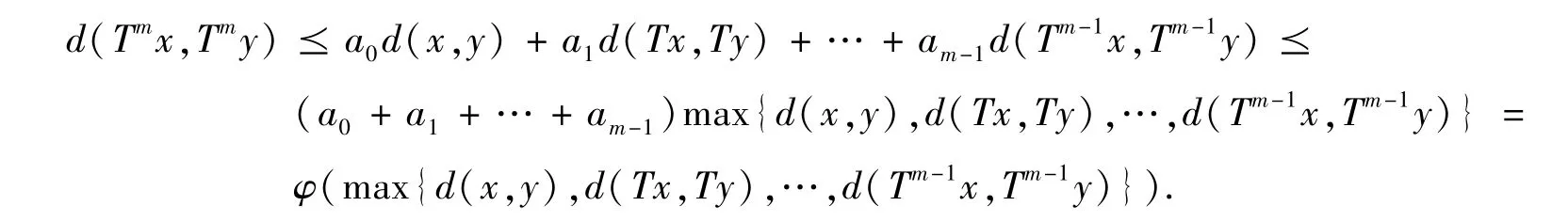
定理1 可知，T 在X 中存在唯一不动点.

特别地，在推论3 中令m ＝2 ，则有

推论4 设(X，d) 是一个完备锥b－度量空间，系数s ≥1 ，P 为X 上的锥，T 是X 到X 的连续映射，且存在m ∈ℕ ，a0，a1∈[0，1) ，0 ≤a0＋a1< 1 ，使得:

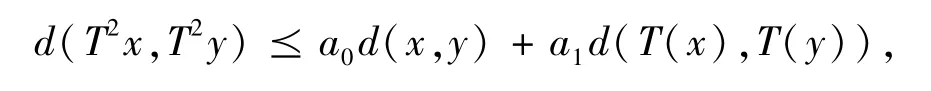
则T 在X 中存在唯一不动点.