一种基于模糊粗糙集的快速特征选择算法

张 晓 杨燕燕

（1.西安理工大学应用数学系，西安，710048；2.清华大学自动化系，北京，100084）

引 言

经典的粗糙集理论[1]是由波兰数学家Pawlak在1982年提出的,它是一种处理数据中的不确定性的有效工具,然而经典粗糙集只能处理符号值(名义值)的数据。模糊粗糙集[2]作为经典粗糙集的最重要的推广之一,可以用来处理实数值甚至是混合值的数据。目前,模糊粗糙集已经成功应用于机器学习和数据挖掘领域[3],其最受人们关注的应用之一就是特征选择(属性约简)。关于模糊粗糙集特征选择的研究工作已存在不少[4-10],但其快速的特征选择算法的研究还很少,据作者所知,仅文献[11]在特征选择算法迭代步骤提供了加速策略，从而减少了算法的计算时间。

实际中的数据一般包含信息量较低的样例或噪声点,如果对样例进行筛选,利用筛选得到的样例进行挖掘知识将会减少计算的复杂度。文献[12]提供了3种样例选择的启发式算法,其中之一的算法思想即选择隶属模糊正域的值不小于给定阈值的那些样例。文献[13]使用一种模糊粗糙度量来刻画样例的质量并给出了wrapper式的样例选择方法。文献[14]针对k-最近邻分类规则提出了一种加权抽样技术来筛选代表样例。事实上,特征选择和样例选择是相对独立的工作,也有一些文献基于模糊粗糙集研究特征和样例同时选择的方法[15-18]。例如,文献[18]给出了一个基于频率的启发式算法来交替选取特征和样例,以达到特征和样例同时被选取的目的。

由于现有的基于模糊粗糙集的特征选择算法的复杂度一般是O(n2m2),其中n为数据集中的样例个数,m为特征个数。当数据集中有较多的样例时,现有的特征选择算法会消耗大量的计算时间和存储空间。注意到特征选择和样例选择还有另外一个结合点,即是先对数据进行样例选择,然后利用筛选的代表样例进行特征选择,从而减少特征选择算法的计算时间。因此,本文是对数据集筛选代表样例进行特征选择达到加速计算的目的,不同于文献[11]在特征选择算法迭代步骤进行加速的策略,这也为特征选择的快速算法提供了一种新的思路。

基于文献[12]中样例选择的思想,本文先对样例进行筛选,即筛选那些模糊下近似值不低于给定阈值的那些样例,然后在文献[7]的基于模糊粗糙集构造信息熵进行特征选择的工作基础上,只利用筛选样例的信息熵进行特征选择以降低算法的复杂度,从而提供了一种快速的特征选择算法。数值试验表明该算法具有有效性,且对筛选样例多少的关键参数给出了合理的建议。

1 预备知识

1.1 模糊粗糙集

设U是一个论域,F(U×U)为U×U上的模糊幂集。如果R∈F(U×U),R称为一个在U×U上的模糊关系。如果对任意的x∈U有R(x,x)=1,R称为是自反的;如果对任意的x,y∈U有R(x,y)=R(y,x),R称为是对称的;如果对任意的x,y,z∈U有R(x,y)≥T(R(x,z),R(z,y)),则R称为是T-传递的,其中T为三角范数。另外,如果R是自反、对称和T-传递的,则称R是U上的一个模糊T-相似关系。

文献[2]在模糊T-相似关系R上给出了模糊集X∈F(U)的一对下、上近似算子：对任意的x∈U

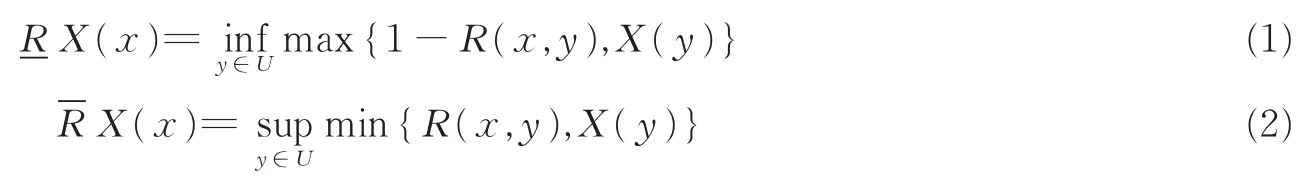
式(1)和式(2)是模糊粗糙集最初的一对下、上近似算子,后来也有不少文献对其进行了推广,而式(1)和式(2)是应用最为广泛的一对近似算子,故本文的研究工作也是在其基础之上展开的。

1.2 模糊信息系统和模糊决策系统

一个模糊信息系统是一个二元组(U,A),其中U={x1,x2,…,xn}为论域,xi为对象(样例);A={a1,a2,…,am}是一个有限非空的属性(特征)集;对于每个a∈A,有一个映射a：U→Va,Va称为属性a的值域,且每个属性a都可定义一个模糊关系R{a}。由任意的属性子集B⊆A可定义一个模糊关系。

一个模糊决策系统是一个二元组(U,A∪D),A∩D=∅,其中(U,A)是一个模糊信息系统,A称为条件属性集,D={d}称为决策属性集,d是符号值的属性,成立一个映射d：U→Vd,且Vd={d(x)：x∈U}称为决策属性d的值域。

在决策属性集D上定义一个等价关系,即

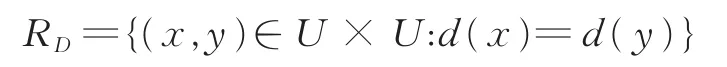
则RD产生U的一族划分

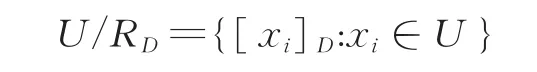
式中[xi]D={xj∈U：(xi,xj)∈RD}称作是对象xi所属的决策类。需要指出的是,分明决策类[xi]D的特征函数为

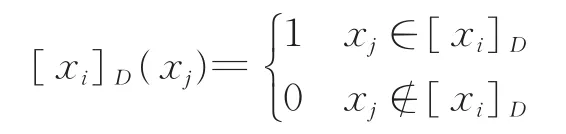
定义1[5]设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},F(U)是U上的模糊幂集。模糊集X∈F(U)的基数定义为

1.3 λ-信息熵

定义2[7]设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},B⊆A。决策属性集D相对于条件属性集B的λ-条件熵定义为

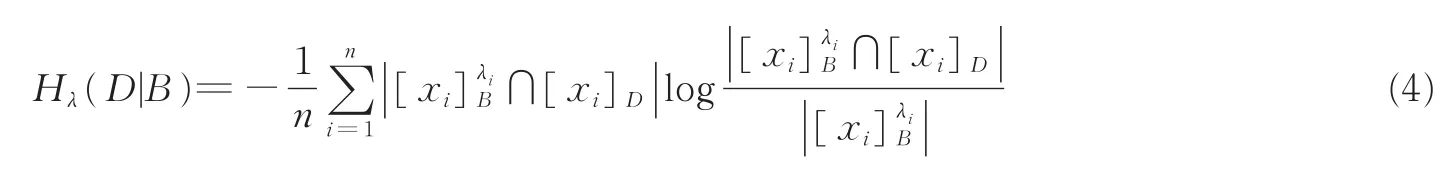
式中

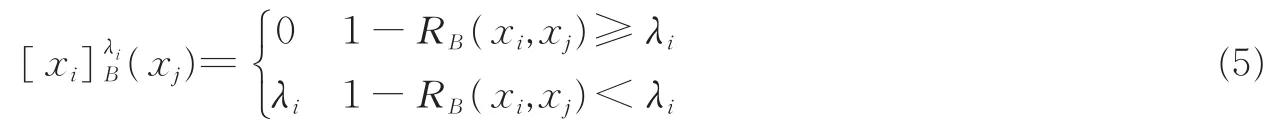
是对象xi关于B的模糊粒,。

注释1[7]如果,在这种情况下,定义

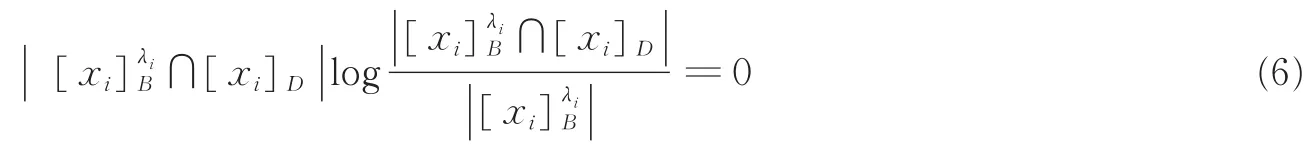
定理1[7]设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},C⊆B⊆A,则

由定理1知,λ-条件熵关于属性子集是单调的。

2 基于模糊决策系统筛选样例的特征选择算法

本节利用文献[12]的样例选择思想,先对模糊决策系统的样例进行筛选,然后利用筛选样例构造新的λ-信息熵,并给出相应的特征选择算法。

设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},属性子集B⊆A。对U中每一个对象(样例)xi(i=1,2,…,n),计算对象xi隶属其所在决策类[xi]D的下近似值。已知度量了对象xi隶属[xi]D的确定程度,因此的值越小,对象xi隶属[xi]D的确定程度越低,这也说明了对象xi包含的不确定信息越多。在实际中,边界点和噪声点包含更多的不确定信息,故隶属其所在的决策类的下近似值可能会很小。如果在数据挖掘过程中忽略掉这些有较小下近似值的样例,那么会减少计算时间。给定阈值α∈[0,1],记

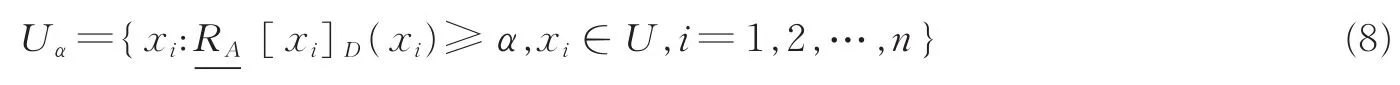
为由参数α确定的(U,A∪D)的筛选样例集。

利用筛选样例集来完成数据挖掘的任务要使最终的结果不能和完整的数据集所得的结果相差太大,因此阈值α要合理地选取。α取值大小直接决定了筛选样例的多少。如果筛选样例过多，从而不能有效地减少计算时间；而筛选样例过少又会损失较多的信息,具体的α取值建议将在数值试验部分给出。

定义3设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},B⊆A,Uα是筛选样例集。决策属性集D相对于条件属性集B的Uα-λ-条件熵定义为

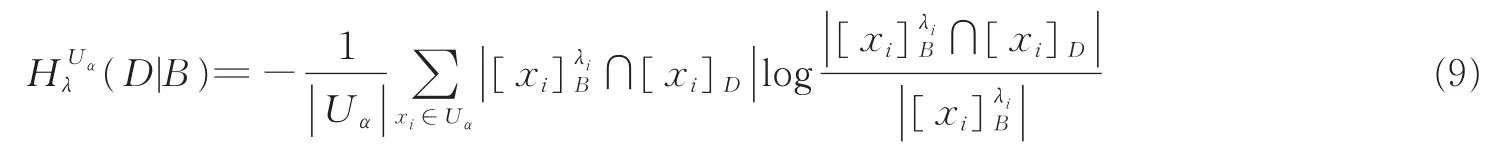
式中|Uα|为Uα的基数。

由定义3易知Uα-λ-条件熵可以看作是λ-条件熵的一种推广,不同之处在于Uα-λ-条件熵只考虑筛选样例的信息熵,而λ-条件熵考虑所有样例的信息熵。因而由定理1知Uα-λ-条件熵也是单调的,即对C⊆B⊆A有。应该指出的是注释1对定义3同样成立,且由文献[7]定理3易知恒成立。

定理2设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},B⊆A,Uα是筛选样例集,则的最大值为|Uα|/e。

证明：由文献[7]定理5易证。

定理3设(U,A∪D)是一个模糊决策系统,U={x1,x2,…,xn},B⊆A,Uα是筛选样例集,则当且仅当对任意的xi∈Uα成立。

证明：由文献[7]定理6易证。

如果一个新的条件属性添加到条件属性子集,则Uα-λ-条件熵就会单调地减少,从而Uα-λ-条件熵减少的值就反映了添加的属性相对条件属性子集的重要程度。

定义4设(U,A∪D)是一个模糊决策系统,B⊆A,Uα是筛选样例集。对任意的条件属性a∈AB,a相对于D对B的Uα-重要性定义为

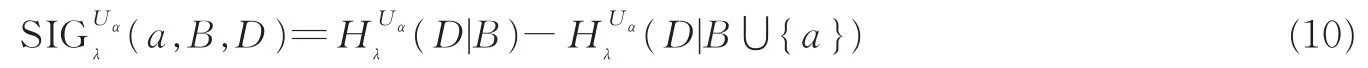
利用Uα-重要性度量,给出相应的特征选择算法。

算法1基于模糊决策系统筛选样例的特征选择算法

输入：模糊决策系统(U,A∪D),U={x1,x2,…,xn},阈值α;

输出：属性子集B

① 初始化Uα=∅。对每一个对象xi∈U,根据式(1)计算。如果λi≥α,添加xi到Uα;

③对每个条件属性aj∈AB,计算;

⑤输出B并终止算法。

该算法的时间复杂度是多项式级的。实际上,该算法第1步的时间复杂度为O(|U|2|A|),第3步的时间复杂度至多为O(|Uα||U||A|)。另外,第3步至多迭代|A|次,第4步的时间复杂度为O(|A|)。综上,算法1的时间复杂度为O(|U||A|(|U|+|Uα||A|))。

3 数值试验

本节通过一些数值试验对算法1的有效性进行评估。试验主要使用算法1搜索1个特征子集,评估参数α对特征选择在特征个数、计算时间及获取精度等方面的影响。为了达到目的,从UCI数据库下载了8个数据集,关于数据集的描述如表1所示。

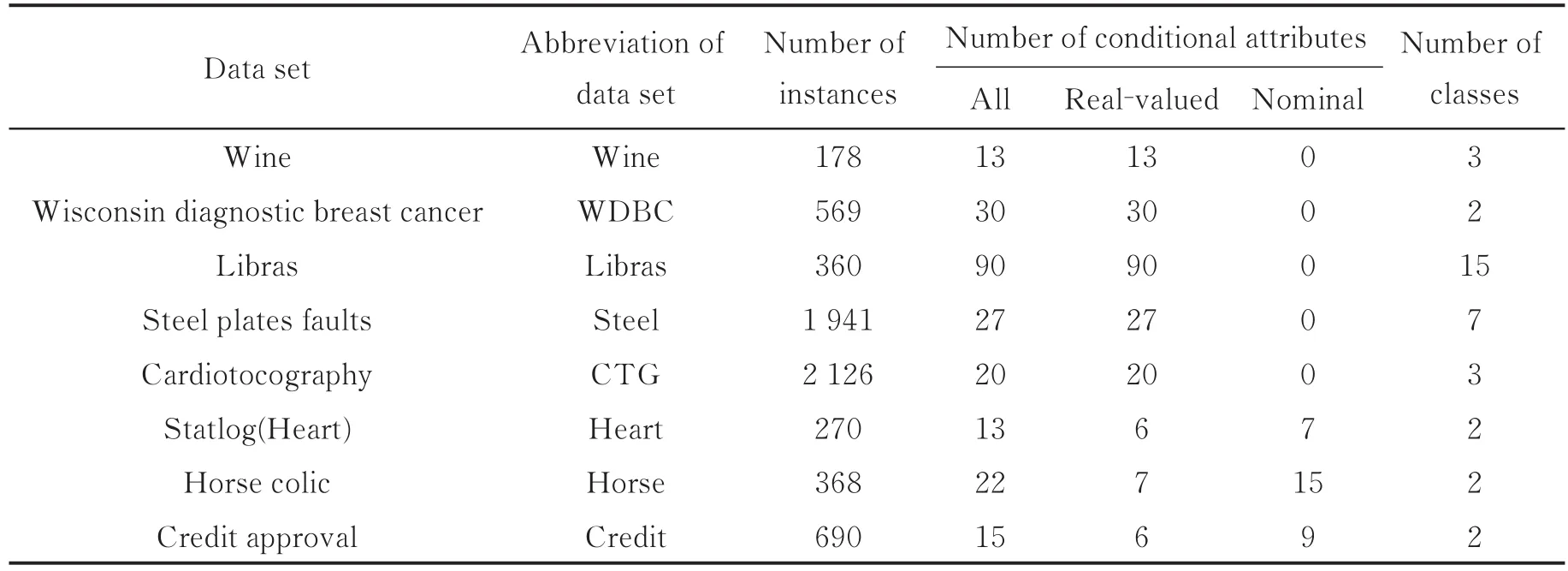
表1 数据集描述Tab.1 Description of data sets

3.1 数据预处理和试验设计

对每个数据集,分别用U，A和D标记论域、条件属性集和决策属性集。如果其中存在一些实数值的条件属性,则对这些属性的属性值先进行标准化,即对实数值的属性a∈A有

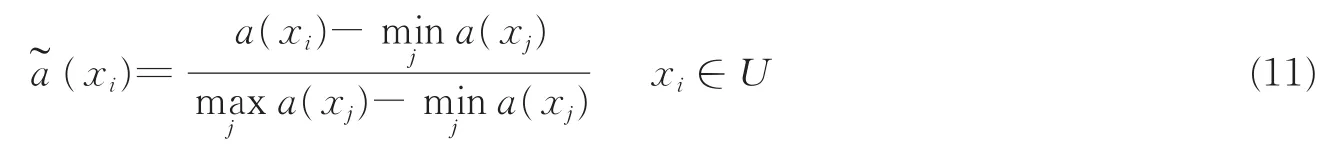
于是对任意的xi∈U，有。这里为了符号的简单,仍然用a标记标准化的条件属性。

试验设计如下：给定一个预处理过的数据集,用十折交叉验证方法得到试验结果。具体地,所有样例被平均等分为10份,每一份轮流作为测试集,剩下的9份作为训练集。对任意一个训练集中的标准化条件属性a，定义一个模糊关系

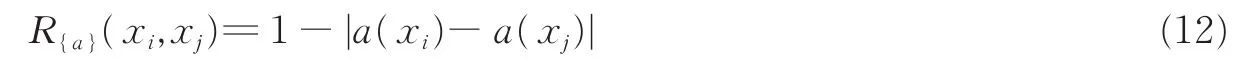
式中xi和xj为该训练集中的对象(样例);若该训练集中有符号值的条件属性a，则定义

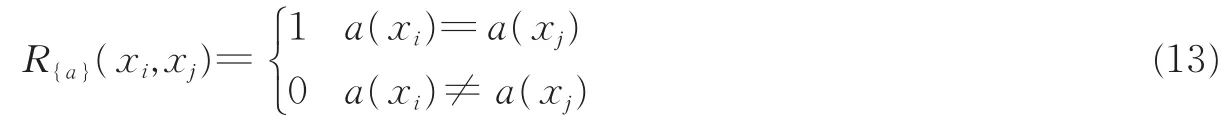
由此每一个训练集都转化为一个模糊决策系统。利用算法1在该训练集上对给定的阈值α选取样例进而选择特征子集。选择的样例和特征子集用来构造k-最近邻分类器(其中k=1,即1NN)和线性支撑向量机(LSVM)，其中分类器的参数均为默认设置。构造好的分类器用来对测试集获取分类精度(测试精度)以检验算法1的有效性。这个过程对每一对训练集和测试集都执行一次,因而最终报告的试验结果是10次试验结果的平均值。

再令筛选样例的阈值α取值范围设置为0到1,步长为0.05。对模糊下近似值进行标准化的原因是需要对所有数据集的α取值统一标准。

3.2 试验结果

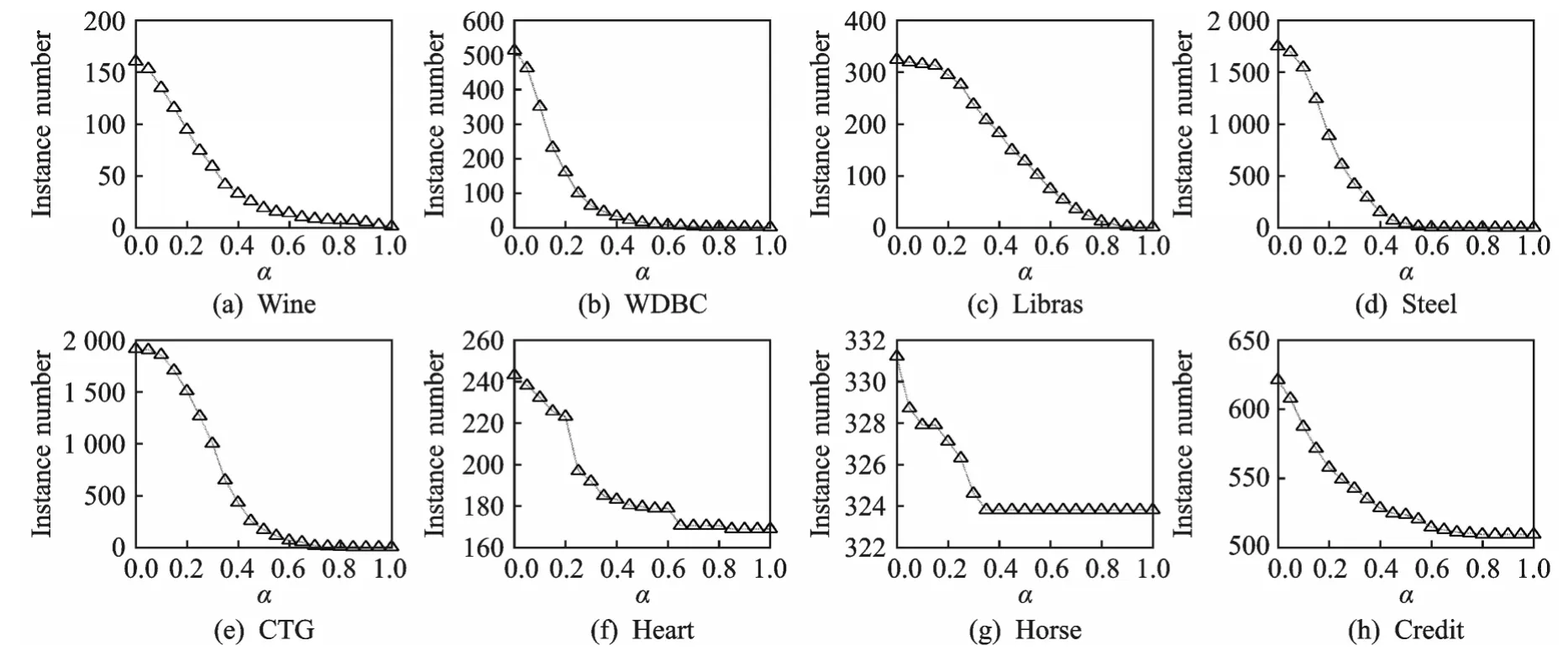
图1 不同阈值α下筛选样例的平均个数Fig.1 Average number of selected instances with different threshold valuesα

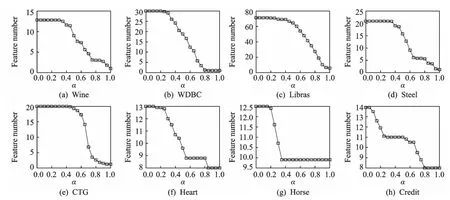
图2 不同阈值α下选择特征的平均个数Fig.2 Average number of selected features with different threshold valuesα

图3 不同阈值α下特征选择过程的平均运行时间Fig.3 Average running time of feature selection process with different threshold valuesα

图1—4分别描述了各个数据集在不同的阈值α下选择的样例的平均个数、选择的特征的平均个数、特征选择的平均时间和获取的平均分类精度。由图1和图2很容易看到随着α值的增加,算法1选择的样例和特征的平均个数都单调地减少。此外,实数值的数据集Wine，WDBC，Libras，Steel和CTG随着α趋于1,选取的样例或特征的平均个数也趋于0;而对另外3个混合数据集Heart，Horse和Credit来说,当α趋于1时选取的样例或特征依然比较多,这也说明了实数值样例的标准化模糊下近似值大多小于1而混合值样例的标准化模糊下近似值大多等于1,这主要由本文针对实数值和符号值的条件属性所定义的模糊关系决定。由图3也容易看到随着α值的增加,特征选择过程的平均运行时间也大致地单调减少,尤其对实数值的数据集Wine，WDBC，Libras，Steel和CTG而言,运行时间在α大致对应的区间(0,0.5)上减少得最快。由图4可以看到,当α趋于1时,实数值的数据集Wine，WDBC，Libras，Steel和CTG获取的分类精度急剧地减少,这是由于α趋于1造成选取的样例和特征过少而导致分类器拟合不足;对于混合数据集Heart，Horse和Credit,阈值α的变化对获取的精度并没有太大影响,这是因为变化的α使得选取的样例和特征仍然比较多，从而仍能较好地训练分类器。

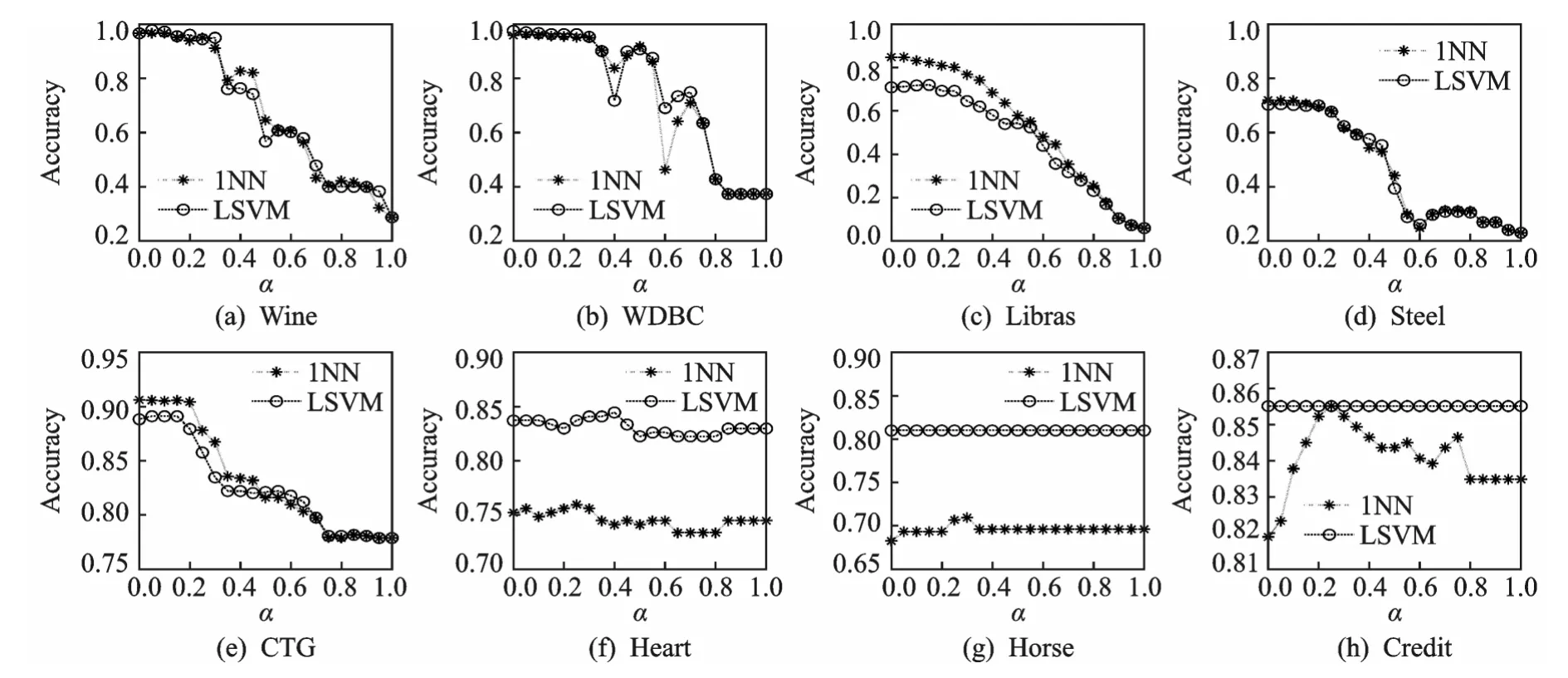
图4 不同阈值α下获取的平均分类精度Fig.4 Average classification accuracy obtained by different threshold valuesα

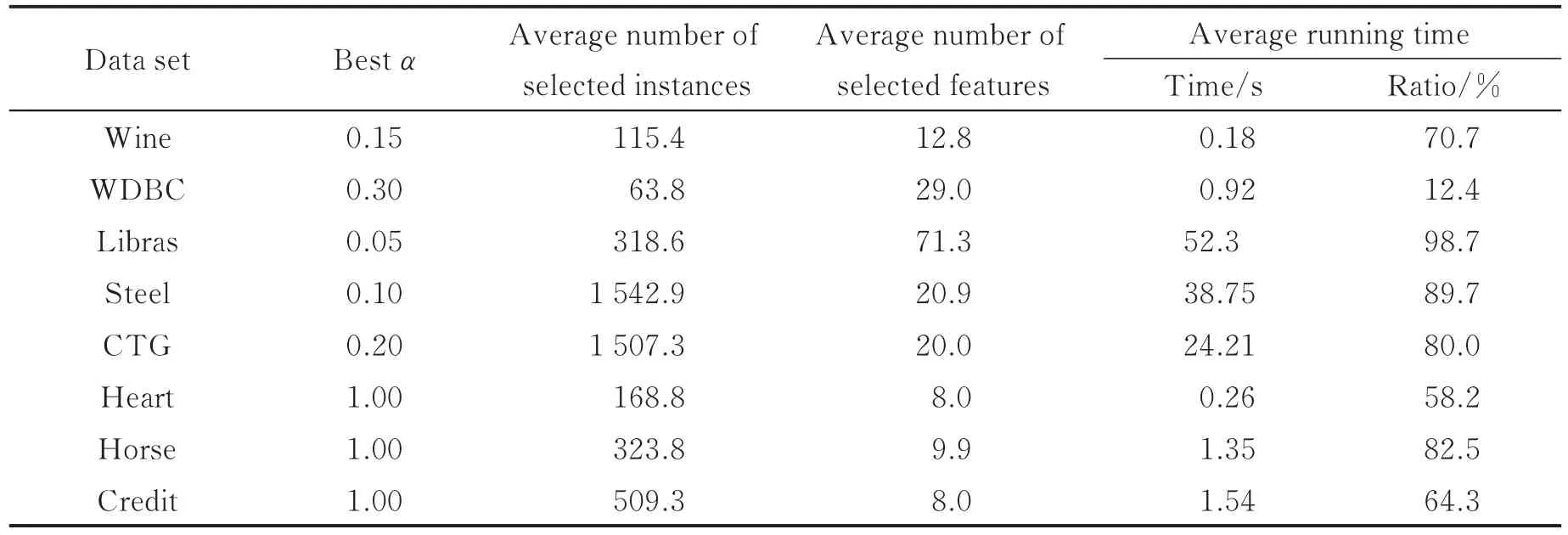
表2 1NN所对应的最佳阈值α及相应的试验结果Tab.2 Best threshold and the related experimental results obtained by 1NN

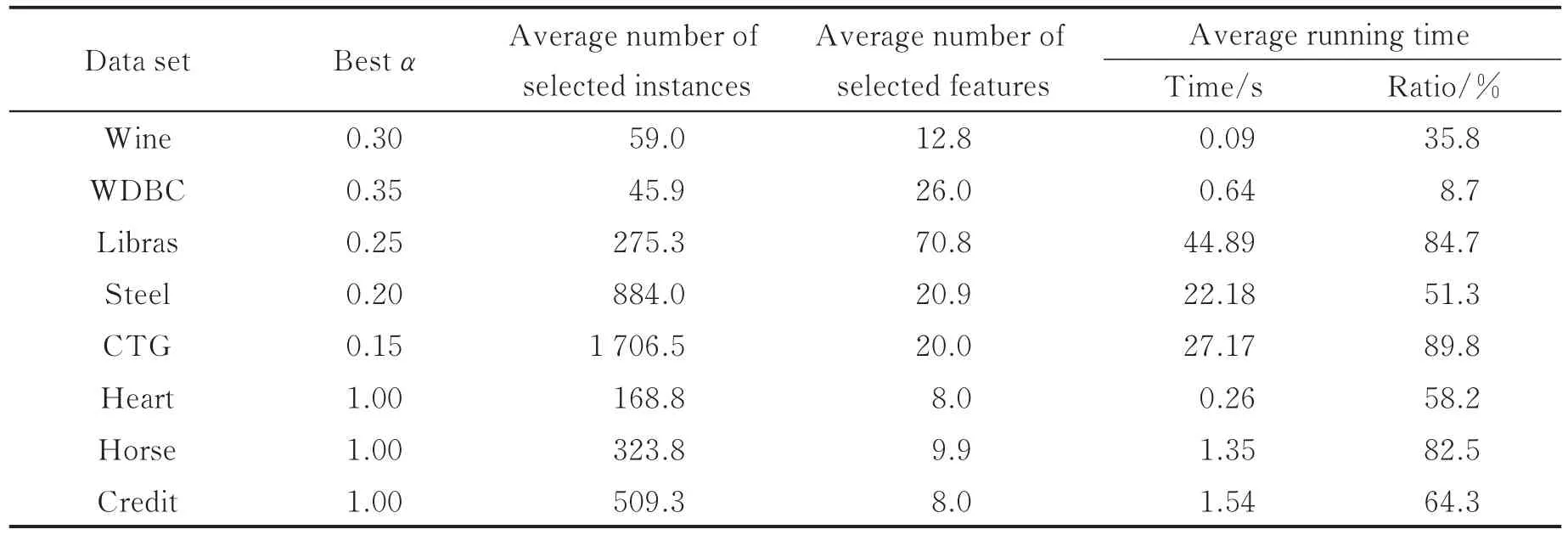
表3 LSVM所对应的最佳阈值α及相应的试验结果Tab.3 Best threshold and the related experimental results obtained by LSVM

从试验结果来看,阈值α的选取至关重要。表2和表3中分别列出在1NN和LSVM下每个数据集所对应的最佳阈值及其相应的试验结果。需要指出的是，这里的最佳阈值是获取的分类精度不会显著低于α=0时所获取的分类精度的最大阈值。这里,采用Paired-t检验来验证分类精度的显著不同,其中显著性水平设为0.05。另外,表2和表3的最后一列指的是最佳阈值下的特征选择时间占α=0时特征选择时间的比例,其值越小则意味着节约的计算时间越多。

综合表2和表3可以看出,对几乎所有数据集而言,最佳阈值α能有效地减少特征选择的计算时间而且对最终获取的分类精度没有显著影响。进一步地,对于实数值的数据集,合理的阈值α大概在区间[0.1,0.3]附近选取;对于混合数据集,阈值α可取为1。

4 结束语

本文提出了一种基于模糊粗糙集的快速特征选择算法,其思想是对样例先进行筛选，然后在筛选样例上进行特征选择。具体地,基于文献[12]的样例选择的思想,本文对模糊决策系统先进行样例筛选,即选择模糊下近似值不低于给定阈值α的那些样例,然后定义了筛选样例的单调信息熵用来作为特征选择的评估度量,并给出了相应的特征选择算法。试验结果表明本文提出的特征选择算法能有效减少计算时间且不会明显降低特征子集所得的精度,另外也分别针对实数值的数据集和混合数据集给出了控制筛选样例个数的阈值α的建议。