模糊函数主脊切面特征提取的局域差分方法
普运伟 马蓝宇 侯文太 张天飞
(1.昆明理工大学计算中心,昆明,650500;2.昆明理工大学信息工程与自动化学院,昆明,650500)
引 言
雷达辐射源信号分选是电子侦察信号处理的关键技术。随着信息化的进程不断加快,越来越多雷达、通信设施及制导武器投入使用,战场电磁环境也愈发复杂。同时,随着新型复杂体制雷达逐渐应用并占据主导地位,雷达工作频率不断提高,调制方式也更为多样。在脉冲密度高、形式复杂多变的信号环境中,依据载频(Radio frequency,RF)、脉冲幅度(Pulse amplitude,PA)、脉冲宽度(Pulse width,PW)、脉冲到达时间(Time of arrival,TOA)和脉冲到达方向(Direction of arrival,DOA)5个常规参数分选和识别雷达信号已变得非常困难[1],探索和补充新的有效分选特征参数已迫在眉睫。
近年来,随着计算机技术的发展,利用雷达信号脉内特征参数对信号进行分选成为可能。研究人员通过小波包特征[2]、时频原子特征[3]、复杂度特征[4]等特征对信号内在调制方式进行分析,进而应用于分选,取得了一些成果。同时,基于雷达指纹的脉冲无意调制特征[5]也取得了一些成果。鉴于模糊函数对信号内在结构信息具有较为完整的描述能力,从模糊函数角度提取新的特征参数有助于对信号进行分选和识别[6-8]。但在分数域上,要想提取所需精度的模糊函数主脊(Ambiguity function main ridge,AFMR)切面,其计算量较大。由于粒子群优化算法具有良好的逐步启发寻优能力且搜索速度快,本文使用改进粒子群算法(Particle swarm optimization,PSO)对雷达信号AFMR切面进行快速提取,然后提取AFMR的局域差分特征,最后采用模糊C均值(Fuzzy C-means algorithm,FCM)算法对所提取的特征参数进行聚类性能研究,并对所提方法的算法复杂度进行对比分析。实验结果表明,相较于文献[8]中基于优势遗传的特征提取方法,本文方法算法复杂度降低了67%,切面搜索速度提高了26%,具有算法简便、搜索速度快、实时性高的优点,可以更好地应对复杂电磁环境。同时,所提取的特征参数差值和、差值最大值和差值分布熵分别较好地反映了模糊函数主脊切面的局域总体性、局域极端性和局域变化性,对雷达信号脉内调制方式具有良好的分辨能力且具有较好的抗噪性能。
1 基于改进PSO的AFMR切面快速提取
1.1 雷达辐射源信号AFMR切面
由文献[6]可知,分数自相关与模糊函数具有如下关系
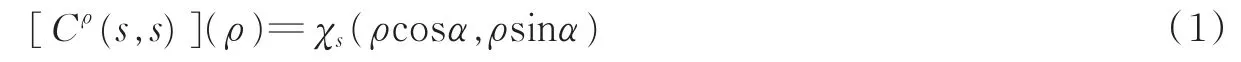
式中:Cρ为旋转角为α的分数域uα上的分数自相关算子;ρ为uα域的径向距离;χs为信号的模糊函数。由式(1)可知,分数自相关相当于对应分数域上模糊函数的径向切面。由此,根据分数傅里叶变换的快速离散方法,便可计算模糊函数任意过原点的径向切面。文献[6]利用上述分数自相关与模糊函数径向切面的关系,定义信号模糊函数过原点的能量主要分布带为AFMR并提出如下检测量
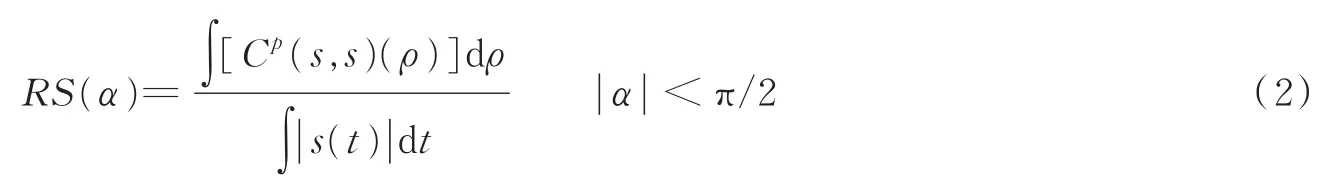
1.2 AFMR切面快速提取的改进PSO方法
PSO算法源于复杂适应系统,是一种通用的全局搜索算法。由于没有交叉和变异运算,PSO算法具有收敛速度快、需调整参数少、易于实现等优点[9]。作为一种基于群智能的进化算法,其应用范围已从最初的函数优化扩展到神经网络训练及工程应用领域[10-11]。为增强AFMR特征提取时效性,本文引入PSO启发式寻优策略以加快AMFR切面的搜索。
本文采用随机惯性权重与自然选择相结合的改进PSO算法进行AFMR切面的搜索,粒子的速度和位置更新公式如下[12]

式中:ω为惯性权重,其大小决定了粒子对当前速度继承的多少;c1,c2为学习因子,决定粒子个体经验和群体经验对例子运行轨迹的影响;pid,pgd分别为个体最优和全局最优;rand1,rand2为在[0,1]范围内均匀分布的随机数。
通过随机初始化产生的粒子群可能会使粒子群位置集中在一定范围内而使最终结果陷入局部最优。为防止这种情况发生,在该方法中初始粒子群位置被设置为均匀分布。均匀分布的初始粒子群还可以让侯选解平均分布在可行解周围,从而使得搜索速度有显著提高。在随机惯性权重参数设置中,ω服从均值为μ,标准差σ为0.5的均匀分布,均值μ服从[0.2,0.9]的均匀分布。均匀分布的ω在算法后期可以避免让粒子被局部极值的吸引[13]从而搜索到较大的AFMR切面值,以保证正确搜索到AFMR切面。同时,在算法过程中,对所有粒子的适应度进行排序,选择适应度高的前50%粒子替代后50%粒子,粒子竞争策略的加入有利于加快算法收敛速度。
根据文献[12]中的对比实验结果可知,改进PSO方法搜索得到的AFMR切面精确度较高,并且较文献[6]方法,改进PSO算法有效降低了搜索雷达信号AFMR切面的时间,平均搜索时间由42.4 s降低至9.8 s,同时在动态信噪比下拥有较好的稳定性。改进PSO算法增强了AFMR切面特征的实用性,也使得其成为信号分选经典五参数的有效补充。
2 AFMR切面特征提取的局域差分方法
文献[6]提取出的雷达辐射源信号AFMR切面特征参数从模糊能量分布的整体角度描述了信号结构上的差异,其采用的矩方法表征了信号AFMR切面模糊能量分布的集中性信息。考虑到各信号模糊函数主脊切面局域方面展现出来的差异性,可对模糊函数主脊切面的局部特性和差异程度进行深入分析,从局部方面描述信号模糊能量分布的差异性信息,挖掘能够表征信号模糊能量分布局域差异性的特征参数。
在低信噪比环境下,为了降低噪声对AFMR切面特征提取的影响,在特征提取之前,对采用点进行滑动平均处理
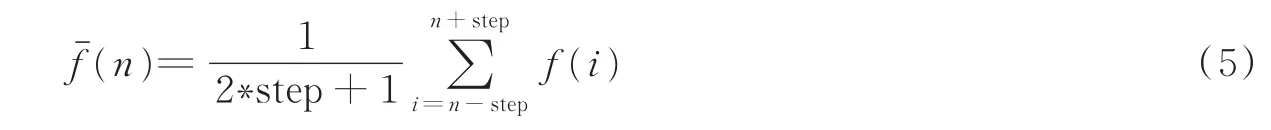
对滑动平均处理后的AFMR切面,采用局域差分方法提取AFMR切面的局域差分特征。其中,局域差分定义为
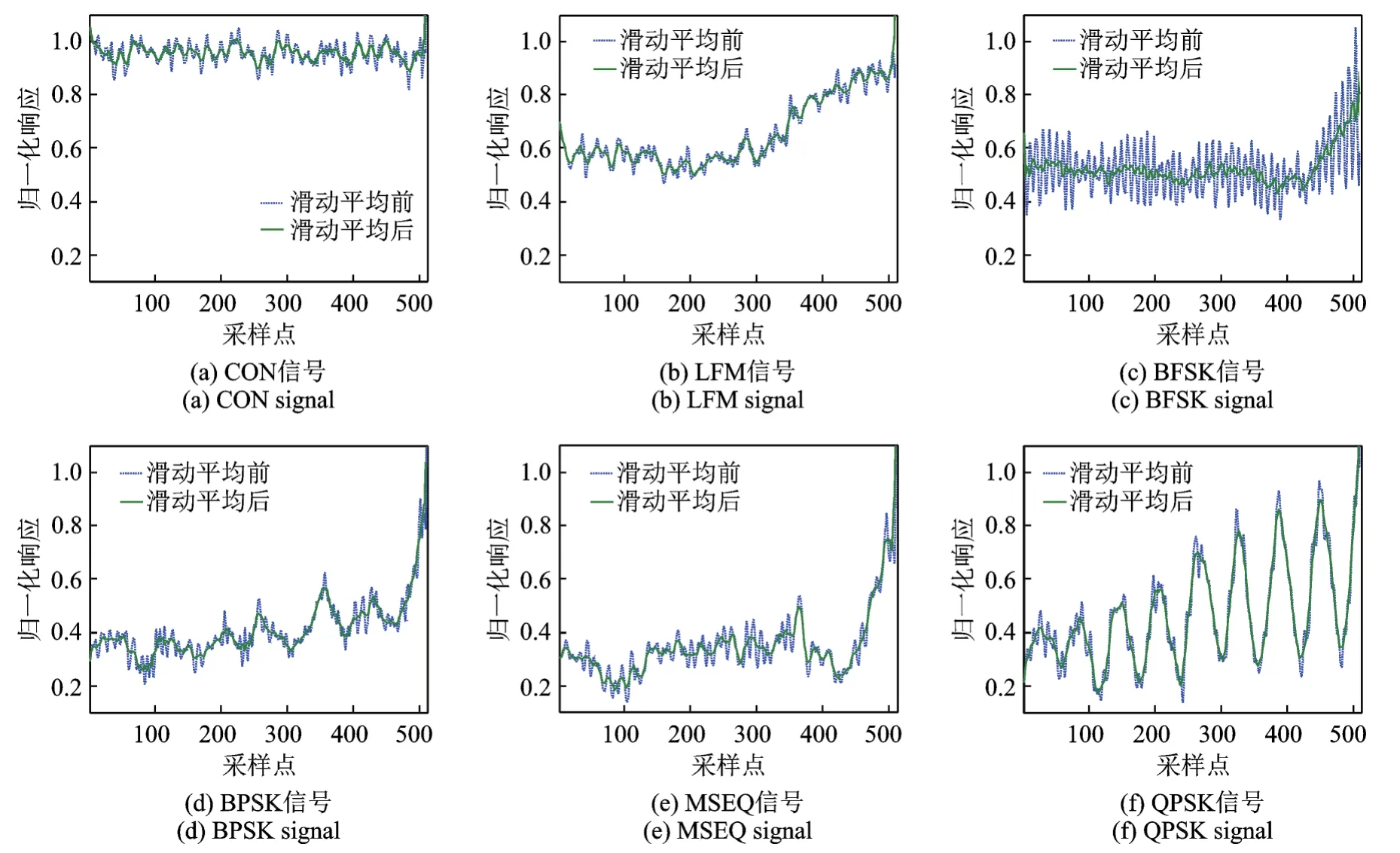
图1 SNR=0 dB,step=5时6种信号AFMR切面滑动平均处理前后对比Fig.1 Comparison of different signal AFMR slides before and after treatment(SNR=0 dB,step=5)
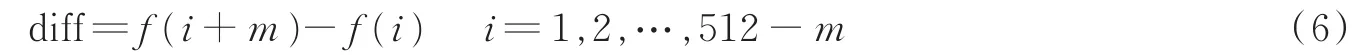
式中diff为AFMR切面上相隔为m的两点模糊能量值之差。
由式(6)所示的局域差分可计算得到512-m个差值diff,之后便可提取3个局域特征参数:差值和(sum_diff)、差值最大值(max_diff)、差值分布熵(entr_diff)。其中,entr_diff的求取方法为:将512-m个差值平均分成t等份,记录每个区域内的差值个数记为x。由此可以统计出每个区域内差值分布概率Pi,进而得到差值分布熵。
可见,局域差分方法所提取的3个局域特征为

由式(7—9)可知:sum_diff统计了AFMR切面差值总和,描述了模糊能量局部变化差异的总体特性;max_diff为AFMR切面局部差异的最大值,描述了模糊能量局部变化差异的极端特性;entr_diff表征了模糊能量主脊切面局部差异的分布特性。
综上所述,本文算法流程图如图2所示。
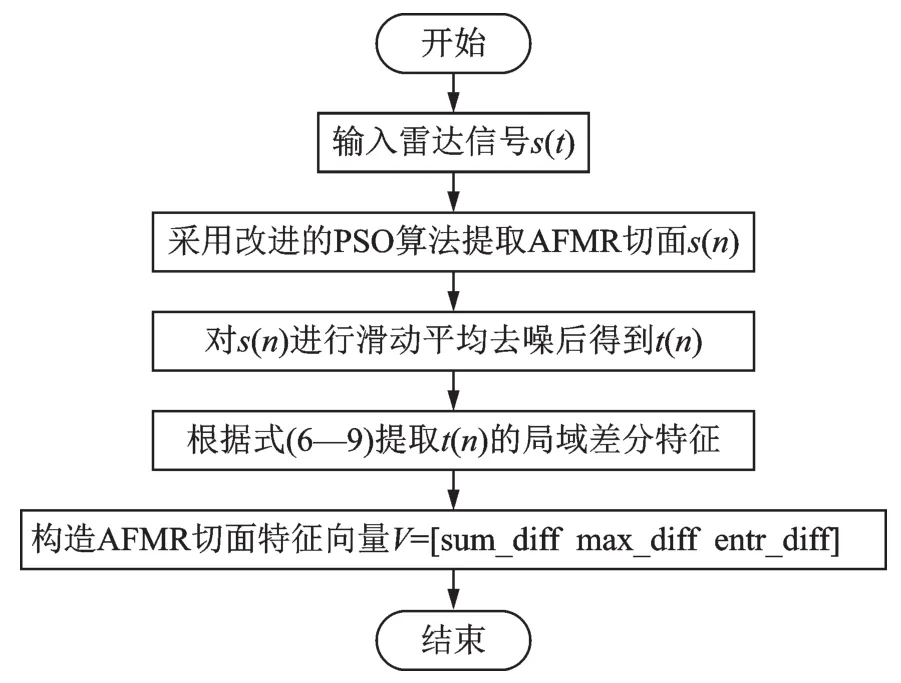
图2 局域差分算法流程图Fig.2 Local difference algorithm flow chart
3 实验结果及分析
为验证本方法的有效性和所提取特征的性能。使用LFM,BFSK,CON,QPSK,MSEQ及BPSK共6种典型信号进行实验,其中LFM的带宽为10 MHz,BPSK和BFSK均为13位Barker码。MSEQ为(1011100),QPSK则采用 16位 Frank码。所有信号PW 均为 10 μs,fs均为60 MHz。另外,除 BFSK的两个频点分别取10 MHz和2 MHz外,其余信号RF均为10 MHz。
在提取AFMR切面的改进PSO算法中,种群规模为20,最大迭代次数为100,ω服从均值为μ,σ=0.5的均匀分布,其中μ又服从[0.2,0.9]上的均匀分布,学习因子c1=c2=1.8。
在局域差分特征提取算法中,为体现典型雷达辐射源信号的局部差异性并尽可能地避免噪声对所提取差值的影响,差值步长m的取值不能太小也不能过大。考虑到信号重采样后数据点个数为512,步长m一般可取为80~90。经过多次测试,在m为85时所提取的特征分离性最好,故在以下实验中,差值步长m为85,差值平均分成60等份。
实验1在0,6,12,20 dB 4种SNR下,每类信号产生100个脉冲,初始相位随机。使用改进的PSO算法对信号的AFMR切面进行快速搜索。为在抑制噪声的同时最大限度保留原始信号信息,对各信噪比下提取出的AFMR切面进行滑动平均处理,step分别设置为2,3,4,5。降噪完成后,采用差值步长m=85提取AFMR差值并将差值分成60等分,依据式(7—9)算出局域差分的3个特征参数sum_diff,max_diff,entr_diff,分别组成固定SNR下的样本容量为600的测试信号集1~4。
使用FCM算法[14]对特征参数进行聚类,对比文献[6]和文献[8]所提特征进行性能分析。图3—6给出了在不同SNR下测试信号集1~4进行FCM聚类后的特征分布情况,每个信号集在相应信噪比下的聚类结果如表1—4所示,与文献[6,8]性能分析对比结果如表5所示。
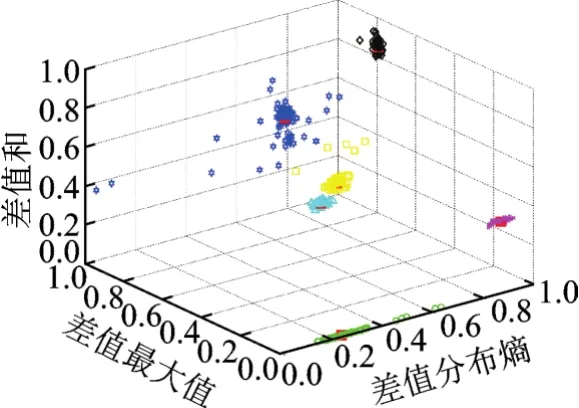
图3 SNR=20 dB时局域差分特征聚类结果Fig.3 Local differential feature clustering results at SNR=20 dB

图4 SNR=12 dB时局域差分特征聚类结果Fig.4 Local differential feature clustering results at SNR=12 dB
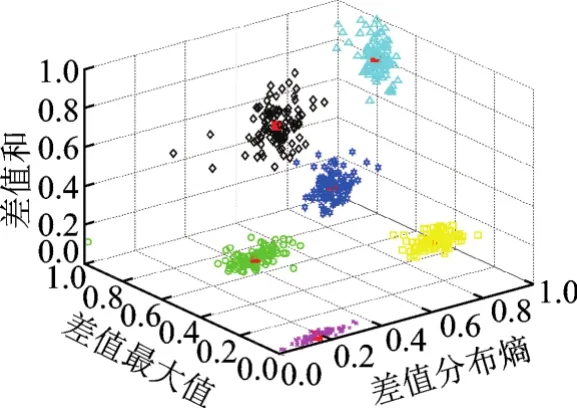
图5 SNR=6 dB时局域差分特征聚类结果Fig.5 Local differential feature clustering results at SNR=6 dB

图6 SNR=0 dB时局域差分特征聚类结果Fig.6 Local differential feature clustering results at SNR=0 dB
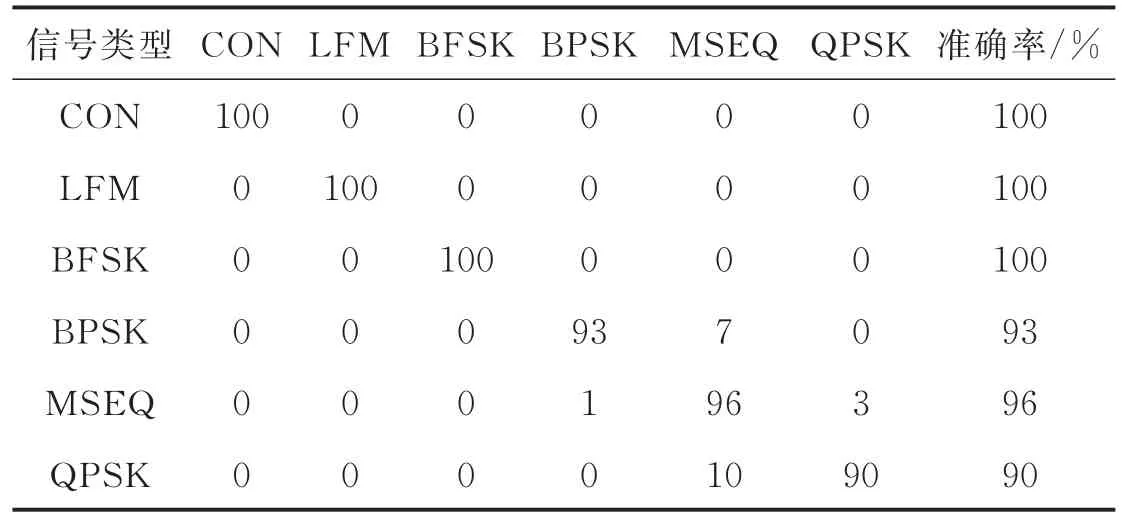
表1 SNR=20 dB时局域差分特征聚类结果Tab.1 Local differential feature clustering results at SNR=20 dB

表2 SNR=12 dB时局域差分特征聚类结果Tab.2 Local differential feature clustering results at SNR=12 dB
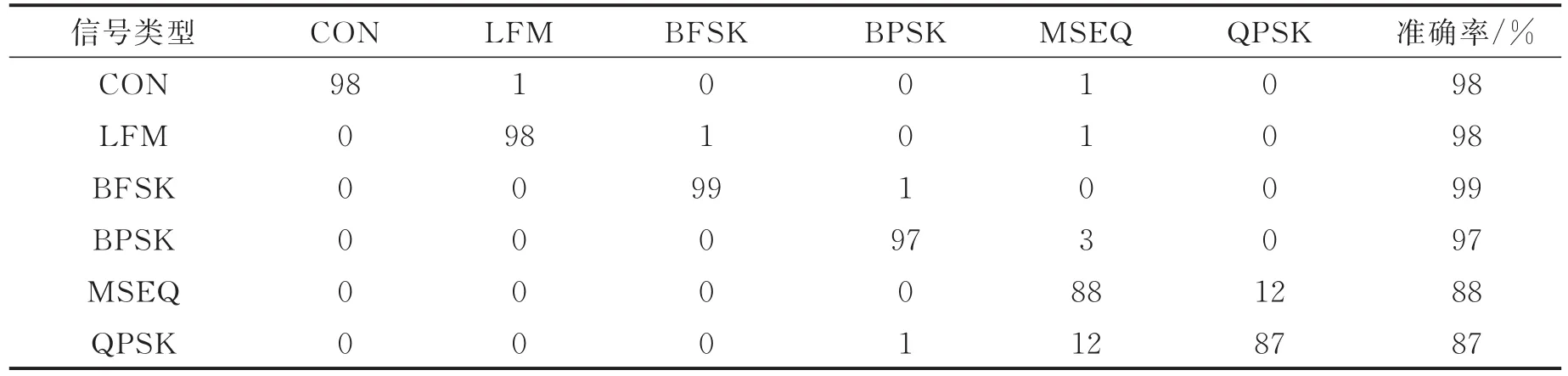
表3 SNR=6 dB时局域差分特征聚类结果Tab.3 Local differential feature clustering results at SNR=6 dB

表4 SNR=0 dB时局域差分特征聚类结果Tab.4 Local differential feature clustering results at SNR=0 dB
由图3—6可知,在不同信噪比下,通过局域差分方法所提取的3个特征均具有较好的类间分离能力和类内聚敛性。在信噪比大于6 dB时,通过FCM聚类图可以看出不同调制类型信号间间隔明显,几乎不存在交叠。
通过表1—4可以看出,在信噪比高于6 dB时,聚类准确率较为理想,最高为100%,最低也达到87%。在6,12,20 dB这3个信噪比下,平均聚类准确率为95.3%,96.8%及96.5%,显示了较好的聚类准确性。即使在信噪比为0 dB时,除了MSEQ,其余信号仍具有较为满意的聚类准确率,平均聚类准确率达到90.0%。表5对本文方法所提取特征与文献[6,8]方法所提取特征的聚类准确性进行了对比。由表5可知,本文方法所提取的特征聚类准确性略低于文献[6]和文献[8],但差距很小,依然保持了93%以上的平均准确性。这说明本文特征提取方法是可行和有效的,所提取的特征参数由于反映了各类信号局域差异,不仅具有良好的类内聚集性和类间辨识能力,且在信噪比发生改变时依然能保持较好的稳定性。
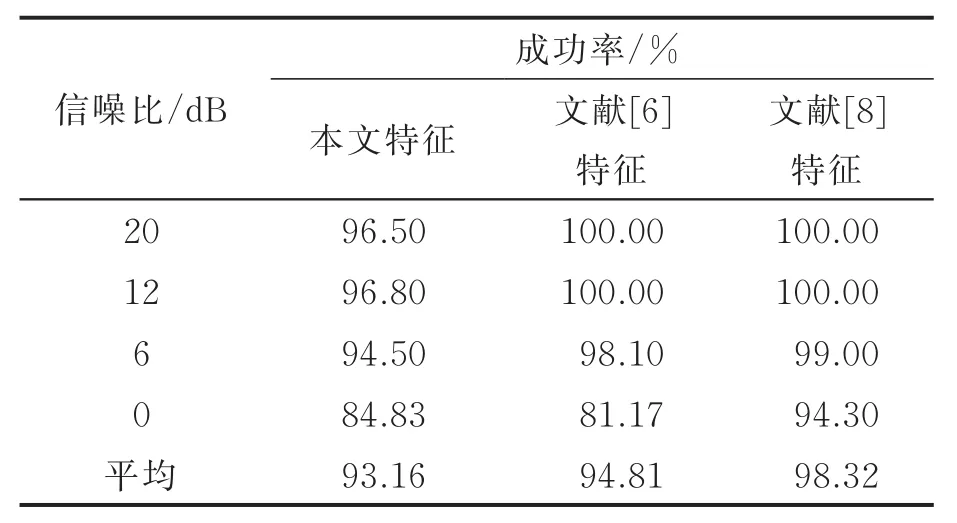
表5 不同特征平均分选成功率对比Tab.5 Comparison of average scores of different features
实验2为验证局域差分特征在信噪比变化时的性能,设置SNR为0,2,4,…,20 dB,每种信噪比下各随机产生10个样本。使用改进的PSO算法对信号模糊函数主脊切面进行搜索,提取出sum_diff,max_diff,entr_diff三个特征参数,组成SNR变化的样本容量为660的测试信号集5。图7给出了信号集5的FCM聚类情况,聚类结果则如表6所示。

图7 SNR为0~20 dB时局域差分特征聚类结果Fig.7 Local differential feature clustering results at SNR=0—20 dB

表6 信噪比0~20 dB下局域差分特征聚类结果Tab.6 Local differential feature clustering results at SNR=0—20 dB
如图7所示,在动态信噪比下6类信号局域差分特征仍然具有较为满意的分离能力,各信号间交叠较小具有明显分隔。通过表6进一步可知,局域差分特征可以适应较大动态型信噪比情形。平均来看,6类信噪聚类准确率为80.5%,其中,LFM信号的聚类准确率最低,为68%,其余各类信号均具有较为满意的聚类准确率,特别是对于BFSK和MSEQ信号,聚类准确率分别为98%和91%。上述实验结果进一步证实了局域差分特征对于SNR变化的稳健性。
由表6可以看出,不同类型信号聚类效果存在差异,其主要原因是噪声对不同信号AFMR切面影响不同。为了说明这一问题,图8给出了LFM信号和BFSK信号分别在信噪比为0 dB和20 dB下模糊函数主脊切面对比图。可见,在两种信噪比下,LFM信号AFMR变化较为明显而BFSK信号AFMR变化较小。由此在动态信噪比实验中,所提取的LFM信号特征值分布较为离散,不同信噪比下特征值差距相对较大,进而在一定程度上影响了聚类效果,而BFSK信号特征值分布较为集中,不同信噪比下特征值差距较小,聚类性能较好。
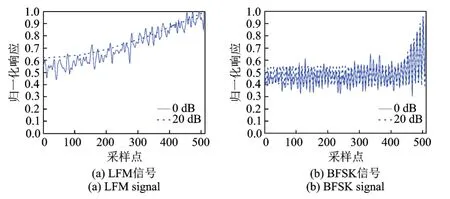
图8 LFM,BFSK信号在SNR为0 dB和20 dB时AFMR切面对比Fig.8 AFMR comparison of BFSK and LFM signals at 20 dB and 0 dB
实验3为考察本文方法提取特征的速度,验证方法的时效性,在SNR=20 dB情况下,6类信号各产生10个随机样本,分别使用局域差分方法、矩方法[6]及图形轮廓方法[8]提取相应特征,并记录特征提取耗时。实验所用计算机配置为:CPU:Intel i5-3230M,内存:8 GB,硬盘:128 GB。实验结果如表7所示。

表7 信号特征提取耗时比较Tab.7 Time-consuming comparison of signal feature extraction s
由表7可见,对比矩方法和图形轮廓方法,本文特征提取方法平均耗时分别减少6.57 s和0.6 s,缩短了79%和26%,显示出了较好的时效性。为进一步说明本文方法在时效性方面的性能,下面引入算法复杂度概念对本文方法、矩方法及图形轮廓方法进行对比分析。
算法复杂度是指将算法在编写成计算机语言后,执行算法所需要和时间和消耗的计算机资源。算法复杂度主要有两种计算方法,一种是统计该算法所有语句的频度之和,另一种是统计算法中所使用的加减乘除次数。本文采用文献[15]所述方法对各算法复杂度进行分析。
矩方法使用穷举法搜索预处理后信号的AFMR切面,并计算该切面的均值、方差以及标准差,其特征算法复杂度为

图形轮廓方法采用坐标变换的方法将AFMR切面曲线变为一个闭合图形,然后对该闭合图形进行平滑去噪,最后描述所得图形轮廓的特征,其特征算法复杂度为

本文特征提取算法的复杂度为
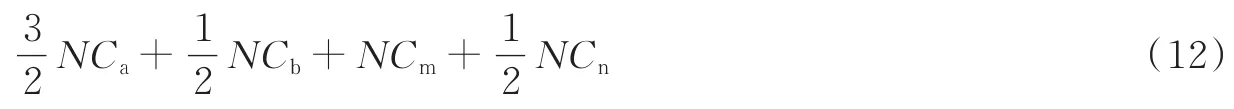
式(10—12)中:Ca为加法运算;Cb为比较运算;Cm为乘法运算;Cn为除法运算。根据文献[15],在大多数情况下,乘法运算与加法、减法运算所需时间和占用计算机资源相差无几,而除法运算耗时和占用资源是上述几种运算的2~10倍。因此上文分析的运算复杂度可转换为乘法数和除法数,如表8所示。
由表8可以看出,本文方法速度较快的主要原因是算法复杂度较低,计算简便。综合来看,本文方法算法复杂度仅约为其他两种方法的1/3和1/6。显然,算法复杂度降低,提高了切面特征提取效率,增强了AFMR特征的时效性,进一步提高了AFMR特征实际工程应用的可能性。
总结上述3个实验的结果可知,基于局域差分方法的模糊函数主脊切面特征提取方法是可行和有效的。所提取的特征差值和、差值最大值、差值分布熵分别描述了信号AF主脊的局域总体性、局域极端性和局域变化性,较好地反映了信号的变化特性。因此,只要信号的AF变化特性不同,该方法均具有较好的信号分辨能力。而且,由于改进PSO算法和局域差分方法具有算法复杂度低、运算量小的优点,因此所提方法具有计算速度快的显著优势,可以保证特征提取的时效性。
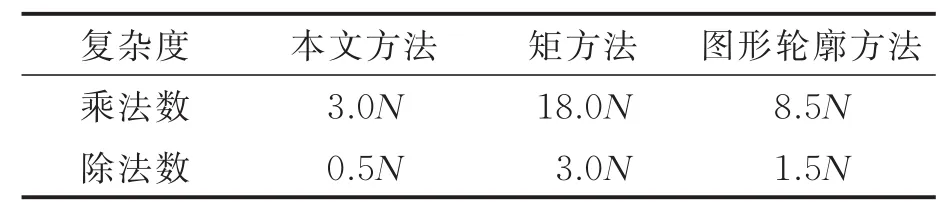
表8 3种算法复杂度比较Tab.8 Comparisons of complexity of three algorithms
4 结束语
围绕复杂体制雷达辐射源信号新特征参数的提取,本文以信号模糊函数主脊切面为研究对象,借助局域差分工具提出了一种新的模糊函数能量主脊切面特征提取新方法。所提方法使用改进PSO算法快速搜索得到模糊函数能量主脊切面,通过局域差分方法提取出差值和,差值最大值和差值分布熵3个特征参数,从而提取出能够表征信号AF主脊能量局域总体性、局域极端性和局域变化性的3个新特征。实验结果表明,所提取的特征参数在信噪比不低于0 dB时均具有较强的信号区分能力,同时还具有较好的抗噪声性能和特征提取时效性。因此,这些特征可以作为雷达辐射源信号分选经典五参数的有效补充。为了进一步改善所提取局域特征在信噪比较低时的性能,后期可以考虑采用基于小波变换、多重分形[16]的信号毛刺去除和基于分数阶Fourier变换[17]等方法对信号进行处理。

