基于异构多中继网络的压缩转发系统

鲍军委 徐大专 张瑞丹 罗 浩

（1.南京航空航天大学电子信息工程学院，南京，211106；2.南京航空航天大学理学院，南京，211106；3.华为技术有限公司南京研究所，南京，210012）

引 言

无线中继技术是无线通信中的一项重要研究内容，它能够有效地抵抗信道衰落、扩大覆盖区域、提高信道容量以及增加分集增益等，因而被广泛地应用到各种无线通信系统中，如卫星通信、移动通信等。近些年来，无线中继技术的研究主要集中于3种策略：放大转发（Amplify-and-forward,AF）、解码转发（Decode-and-forward,DF）和压缩转发（Compress-and-forward,CF）。对于放大转发[1-2]，中继节点只是将信源节点发送过来的信号简单地放大并转发出去。这种策略的弊端在于，传输过程中产生的噪声也会被同时放大并转发。而对于解码转发[3-5]，中继节点将接收到的信源节点信息进行解调和译码后，再重新编码并转发给目的节点，但在译码过程中产生的错误会继续向后传播造成性能恶化。对于压缩转发[6-7]，目的节点需要同时利用来自信源节点的直传信号和来自中继节点的压缩信号进行联合译码，它虽然可以有效地避免错误传播，但需要在信源节点和目的节点之间存在直传路径。另外，由于并联的无线多中继节点可以在目的节点形成虚拟天线阵列，具有空间分集的效果，从而能够有效地抵抗多径衰落带来的影响，提高无线通信的可靠性。多中继技术已成为当今重要的研究对象，其研究内容主要集中在中继节点选择[8-9]、信源节点与中继节点之间的功率分配[10-11]、中断概率分析[12-14]、波束成形[15]以及信道容量[16]等方面。

传感器是现代世界中感受被测量物理量的一种重要装置，将一定数量的无线传感器按特定的方式去采集所需要的数据，并将其传输到某节点进行综合处理，就构成了无线传感器网络。当前，无线传感器网络在军事侦察[17]、环境监测[18]、智能家居[19]、医疗卫生[20]以及智能交通[21]等方面得到了广泛的应用，使得相应的模拟中继网络的研究越来越重要。但是到目前为止，对模拟信号通过多中继网络进行压缩转发的研究还很少见。高斯信源(Chief executive officer,CEO)问题[22]研究了在中继节点进行分布式压缩编码之后的率失真区域和码率问题，却并没有研究整个传感通信网络的传输性能。文献[23]提出了一种模拟高斯信源节点通过多中继网络进行压缩转发的系统模型，并在CEO问题的帮助下，得到了在多个中继节点状态完全相同时的系统的传输性能。

基于多中继网络，本文研究了一种新型的压缩转发系统模型。该模型包括一个信源节点，一个目的节点和L个工作环境各不相同的中继节点。其信源节点发射的是模拟信号，目的节点接收的是数字信号，中继节点则是将模拟信号进行抽样、编码和压缩，转换成数字信号并转发给目的节点，从而完成信源节点和目的节点之间的通信。即该模型可视为由无线传感器网络和无线数字通信网络两部分构成，信源节点和中继节点为无线传感器网络，中继节点到目的节点为无线数字通信网。借助于高斯信源的CEO问题和香农信道容量理论，给出了此系统模型的理论分析框架，并推导出了该模型的表达式。最后，结合无线传感器总功率受限的情况，在总功率约束下，对各中继节点及信源节点进行功率分配，使得系统信噪比性能最佳。

1 传统的多中继放大转发系统模型及功率分配

1.1 系统模型

图1为传统的多中继放大转发系统模型。假设信源节点S发出的模拟信号X(t)服从分布，而信源节点与中继节点之间的所有信道均为加性高斯白噪声（Additive white Gaussian noise,AWGN）信道，则中继节点Ri接收到的信号为

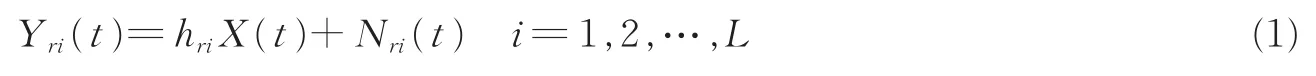
式中：hri为第i个信源节点-中继节点链路中的信道系数，Nri(t)为零均值、方差为的独立同分布（Independently and identically distributed,i.i.d.）的高斯白噪声。中继节点Ri接收到的信号的功率为

每个中继节点将接收到的信号进行功率放大，假设功率放大因子为βi，则发射功率Pri为

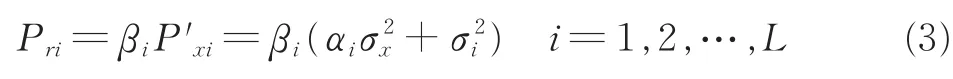
各中继节点通过加性高斯白噪声信道将放大后的信号转发给目的节点。假设中继节点-目的节点链路的信道系数为hdi，则目的节点接收到来自各信道的对应信号及功率分别为

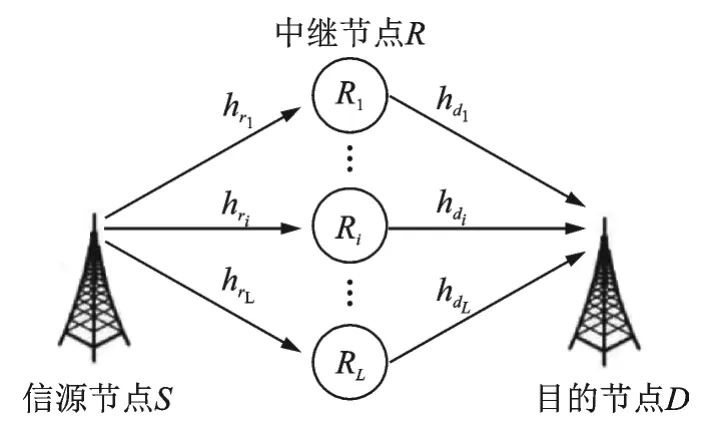
图1 多中继放大转发系统理论模型Fig.1 Theoretical model of amplify-andforward system based on multi-relay network

1.2 功率分配

当中继节点数量大于1时，每条信源节点-中继节点-目的节点链路都类似于单中继的放大转发。目的节点对所有链路的信号进行最大比合并后，生成的信号为

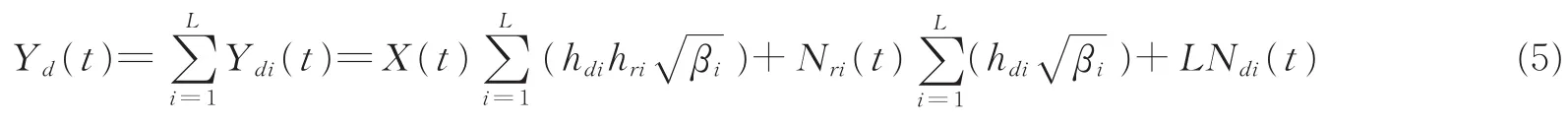
假设各条信源节点-中继节点链路的信道系数hri都相等，即αi=α；各条中继节点-目的节点链路的信道系数hdi也都相等，即μi=μ，则系统最终收到的信号Yd(t)的信噪比为

如果系统总功率P为定值，即

式中Pr为所有中继节点发出的信号的功率和，根据式(3)可以得到

则系统信噪比为

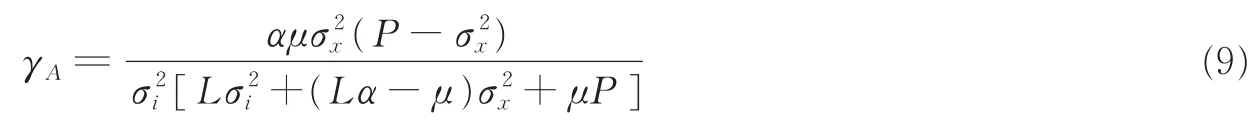
由式(9)可以看出，系统信噪比γA为信源节点发射功率的函数。将γA对求导，并令，可以得到当系统信噪比最大时，信源节点发射功率为

将式(10)代入式(9)，即可得到放大转发系统的最大信噪比(γA)max。

2 分布式多中继压缩转发系统模型及理论分析

2.1 系统模型

图2为本文所提出的多中继压缩转发系统模型。假设信源节点S发出的是服从分布的模拟信号X(t)，信源节点与中继节点之间以及中继节点与目的节点之间的信道均为加性高斯白噪声信道，信道系数分别为hri和hdi，每个中继节点以及目的节点的系统噪声Nri(t)和Ndi(t)均为零均值、方差为的独立同分布的高斯白噪声，则中继节点Ri接收到的信号以及信号的功率分别为

每个中继节点各自利用编码器将接收到的模拟信号Yri(t)进行抽样、编码和压缩，转换成数字信号Y′ri(t)，然后以功率Pri将其转发给目的节点D。目的节点收到的来自中继节点Ri的信号及对应的功率分别为

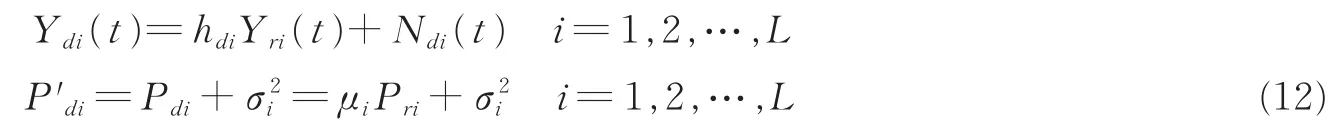
目的节点将来自所有中继节点的数字信号进行合并译码，并将信源节点信号X(t)的估计值输出。至此，完成信源节点与目的节点之间的通信。

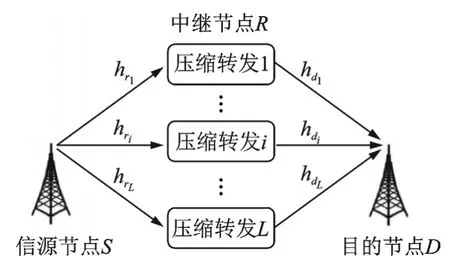
图2 多中继压缩转发系统理论模型Fig.2 Theoretical model of compress-andforward system based on multi-relay network

2.2 基于高斯CEO问题的理论分析

CEO问题是分布式信源编码的一种特例。假设有公司的首席执行官，即CEO，对一些数据感兴趣，而他却无法直接观察到，所以他雇用了一些代理人各自独立地观察这些数据，并各自对观察结果进行处理后报告给他。由于CEO比较忙，所以每个代理人提交的报告要有长度限制。因而，如何使报告内容尽量少，而且失真还尽量地小，是一个值得研究的问题。如果将本模型中对模拟信号进行抽样、编码的中继节点比作同样数量的代理人，将压缩编码比作书写报告，将压缩编码后得到的信息速率比作为所提交的报告的长度，将目的节点的数据处理中心比作CEO，则本系统模型就可作为CEO问题来处理[23]。CEO问题研究的目的在于当中继节点数量L趋近于无穷多个时，如何在总的信息速率和失真之间给出适当的权衡。

高斯CEO问题适用于信源与噪声均服从高斯分布的情况，能够在一定的失真约束条件下，给出中继节点进行分布式信源编码后的率失真区域和码率。根据文献[24,25]中的结论，高斯CEO问题对应的Berger-Tung内界可以表示为

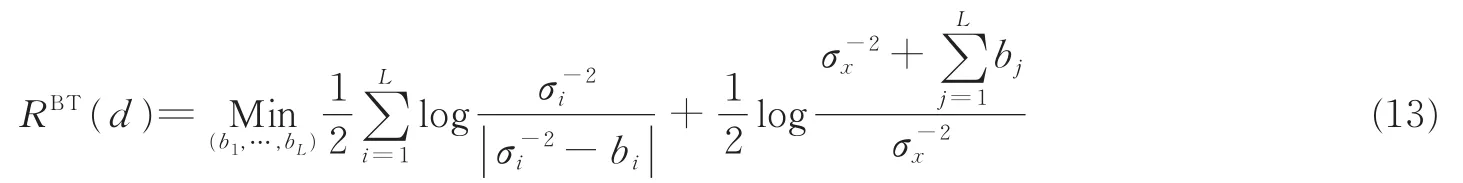
式中：bi(i=1,2,…,L)为优化因子，其可行域为[26]

这里，可行域如果取

会使得R(d)=∞，从而失去理论意义。

根据Berger-Tung内界，有

式中：R(d)为在失真度d下所有可达码率的下界。而由文献[27]可知

因而，有

利用拉格朗日乘子法，可得

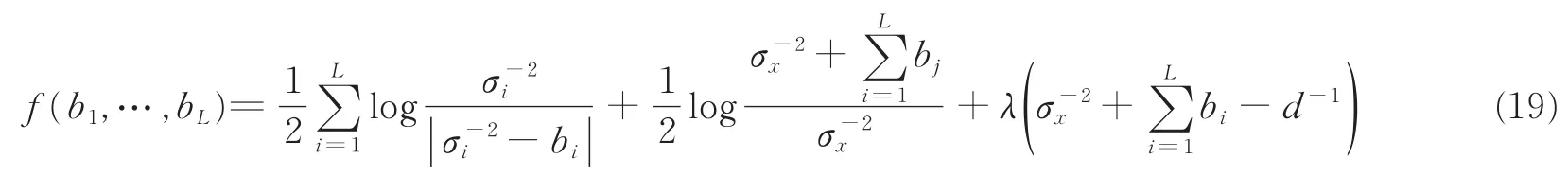
将f对bi求导，再令，可以得到

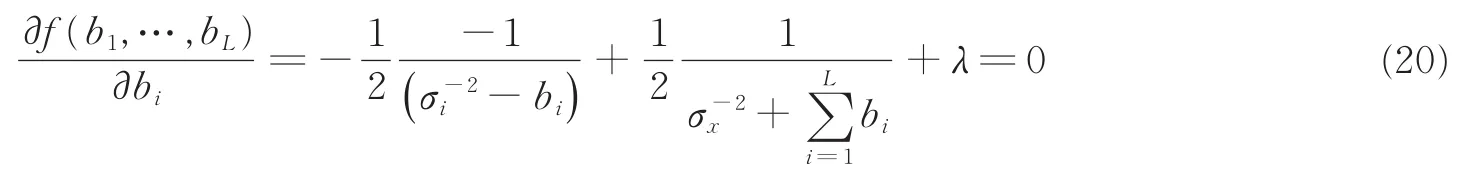
即

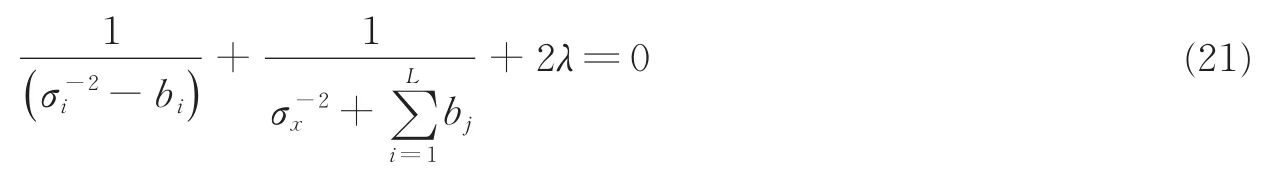
当R(d)达到最小压缩速率时，失真必然会达到最大，即

将式(22)代入式(21)，可得

当中继节点数量多于1时，对式(24)求和可得

再将式(26)代入式(22)，可得

将式(28)代入式(25)，得

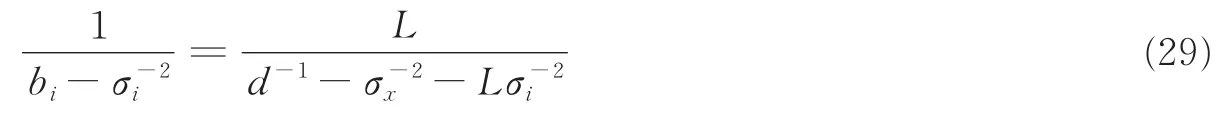
再将式(29)代入式(18)，可得

在本系统中，R(d)表示在失真度d允许的范围内，中继节点对信号进行分布式信源编码后的率失真函数，即信源节点发射的模拟信号到达中继节点时，所有中继节点对其进行分布式编码后的总体最小传输速率。而对于多中继的分布式压缩转发系统而言，每条信源节点-中继节点-目的节点链路，都相当于一个单中继节点的压缩转发系统。另外，是信源节点发射信号X(t)的功率，但实际上，中继节点Ri实际接收到的功率为，对应的信号传输速率为

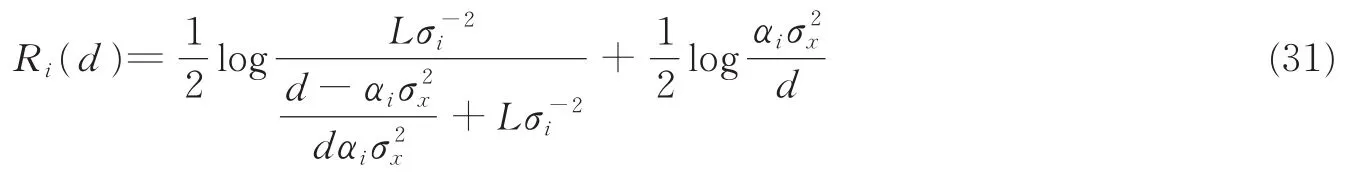
这里，用来衡量系统性能的是量化信噪比γD。这是因为，信源节点发出的是模拟信号X(t)，而目的节点收到并且无失真地恢复出来的数字信号Y′ri(t)，本质上也是从信源节点的模拟信号X(t)抽样、编码和压缩得到的，其过程中产生的失真相似于模拟信号在噪声信道中的噪声干扰。结合量化信噪比，则式(31)变为

2.3 压缩转发系统的联合设计

中继节点Ri将数字信号Y′ri(t)以功率Pri发送给目的节点，根据香农信道理论，中继节点-目的节点链路的信道容量为

式中：μi为信道系数。为了保证信源信息能够完全被传送到中继节点，并且中继节点与目的节点间的信道容量被充分利用，应该有

将式(32)和式(33)代入，有

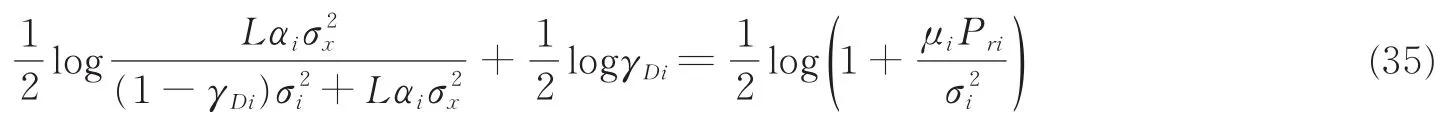
将其简化后可得

对于很多传感器网络，当使用电池供电时，总的功率是一定的，因此有

结合式(37)的功率约束，则系统模型为

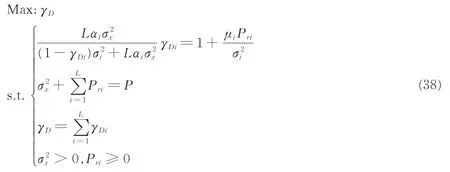
为了表示各个中继节点分配到的功率，令

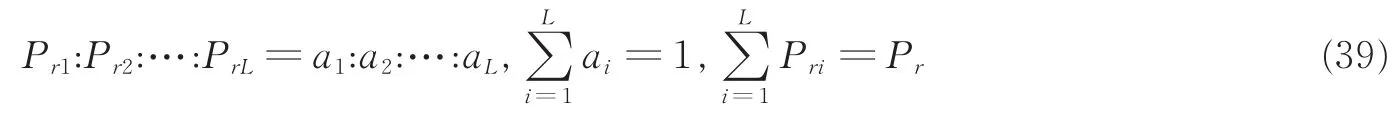
式中：Pr为所有中继节点分配到的功率，则有

将式(40)代入式(38)中第2式，然后再代入第1式，可得系统模型为

2.4 压缩转发系统的性能分析

将此时该压缩转发系统某条信源节点-中继节点-目的节点链路的信噪比性能，与同条件下放大转发系统的性能相比较，即，将式(41)中的第1式与式(9)相比较，可以得到

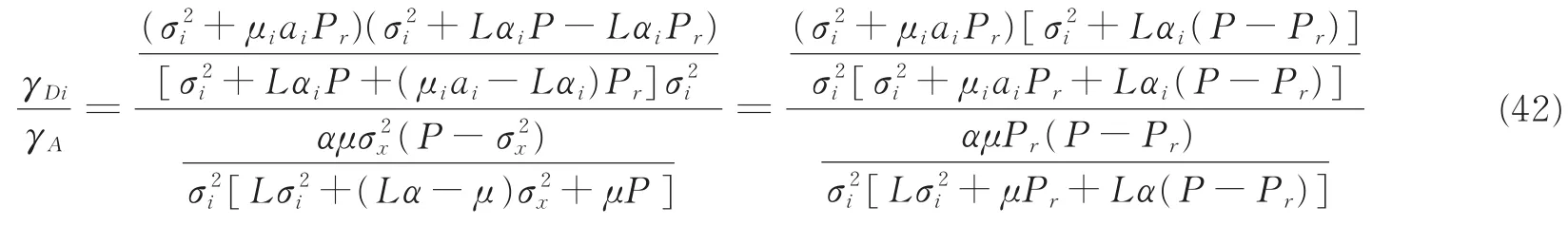
若L=1，有a1=1，令αi=α、μi=μ，式(42)可简化为

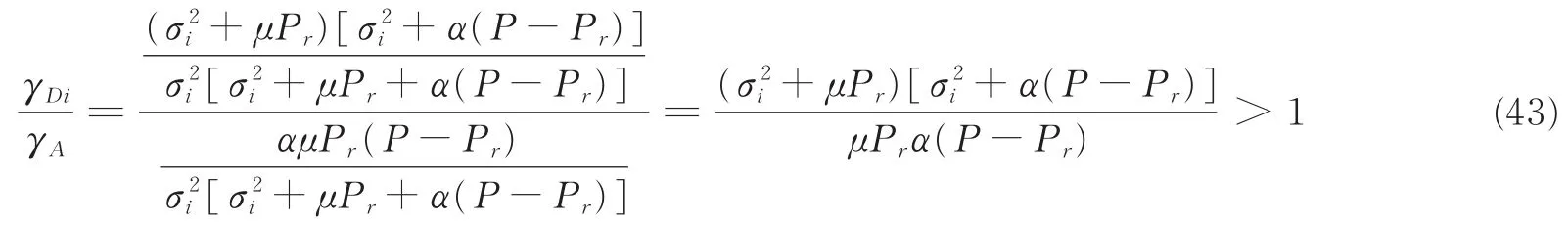
由式(43)可知，当中继节点数量L=1时，压缩转发系统的信噪比性能要优于放大转发系统的信噪比性能。在实际中，中继节点数量往往不止一个，而且各个中继节点的工作环境并不会完全一致，因而每个中继节点的发射功率也应该互不相同。但为简单起见，令

即，各个中继节点分配到的发射功率呈等差数列分布。另外，当噪声的功率远小于系统总功率P时，在式(42)中将忽略，则可得

从式(45)可以看出，对于任意L＞ 1，总有LaiμPr＞aiμPr；另外，对于第L个中继节点，始终存在LaL＞ 1，即始终有LaLLα(P-Pr)＞Lα(P-Pr)。也就是说，对于第L个中继节点，有γDL＞γA。所以，结合式(41)中第2式可知，对于任意的L＞1，始终有γD＞γA。再结合式(43)，从而可以得到结论，当信道条件相同，系统的总功率约束和中继节点的数量也分别相同时，压缩转发系统的信噪比性能优于放大转发系统的信噪比性能。

3 仿真结果及分析

图3给出了当系统总功率分别为0.1，0.3和0.5 W时，放大转发系统与压缩转发系统的信噪比随中继节点数量的变化规律。从图3中可以看出，当中继节点数量从1增加到10时，两种转发系统在目的节点的信噪比都会相应增大，放大转发的信噪比从大约-9 dB，-3 dB和0 dB分别增加到大概-8 dB，0 dB和3 dB，而压缩转发的信噪比则是从0 dB，4 dB和7 dB分别增加到25 dB左右。即，压缩转发系统信噪比无论是在增速还是在数值上，总是高于放大转发的情况。图4对比了中继节点数量分别为2,6和10时，放大转发系统与压缩转发系统的信噪比随系统总功率的变化。很明显，当系统总功率从0.1 W增加到1.0 W时，两种系统的信噪比都会随之增加。放大转发系统的信噪比增加经过了一个先快后慢的过程，从-7 dB左右增加到5～6 dB，而压缩转发系统的信噪比则基本呈线性增加，从8 dB，18 dB和24 dB分别增加到17 dB，25 dB和28 dB。另外，压缩转发的信噪比总是高于放大转发的信噪比。

结合图3和图4发现，无论是中继节点数量增加，还是系统总功率增加，两种系统在目的节点的信噪比都随之增加，但压缩转发系统的增加速度要快于放大转发系统。同时，当中继节点数量增加时，相对于压缩转发的信噪比大幅增加，放大转发的信噪比增加很少。另外，当中继节点数量或者是系统总功率相同时，压缩转发系统在目的节点的信噪比总是大于放大转发的情况。因而，相对于中继直接将信号进行放大和转发，在中继节点处对模拟信号进行量化、压缩和转发，可以在条件相同的情况下，提高目的节点的信噪比或整个系统信息传输的可靠性。或者，压缩转发系统可以在同样的系统性能要求下，降低发送信号的功率，从而延长某些电池供电系统的使用生命周期。

图5给出的是每个中继节点分配到的功率相同和不相同时，压缩转发系统的信噪比性能随中继节点数量的变化情况。从图5中可以看出，当每个中继节点分配到的功率不相同时，系统的信噪比性能略高于每个中继节点分配到的功率相同的情况。而且，随着系统总功率从0.1 W增加到0.5 W，两种情况对应的性能差距略有增大。

4 结束语

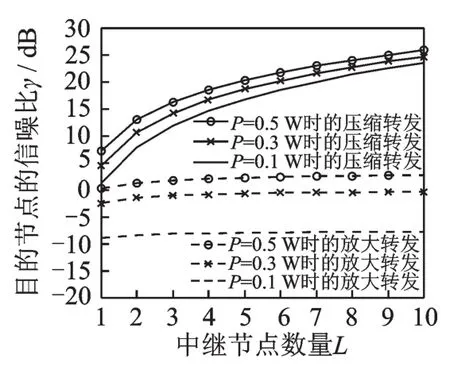
图3 两种系统的信噪比性能随中继节点数量的变化Fig.3 SNR performance curves of the two systems versus the number of relay nodes

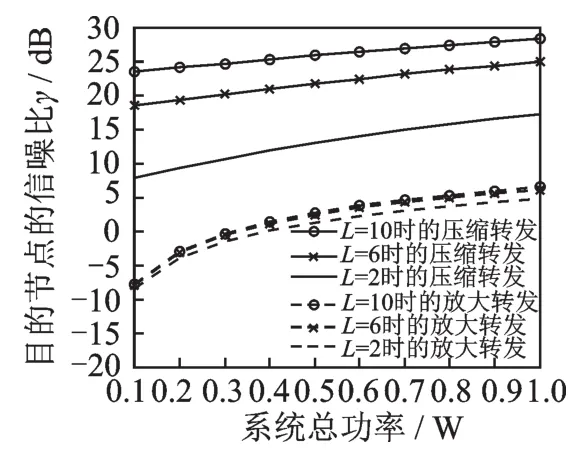
图4 两种系统的信噪比性能随系统总功率的变化Fig.4 SNR performance curves of the two systems versus total system power

图5 压缩转发系统的信噪比性能随中继节点数量的变化Fig.5 SNR performance curves of the compress-and-forward systems versus the number of relay nodes

本文提出了一种新的多中继压缩转发系统模型，其信源节点发射出的是服从高斯分布的模拟信号，目的节点接收到的为数字信号，信源节点和目的节点之间的通信需要借助多个状态不同的中继节点对信源节点信号进行抽样、编码、压缩和转发来完成。借助于CEO理论，推导出各个中继节点处的信息速率，然后结合香农信道容量理论，建立了该系统的理论模型。在总功率受限、各中继节点发射功率不同的情况下，给出了使系统信噪比性能达到最大时的表达式，并与同条件下放大转发系统的性能进行了对比与分析。仿真结果表明，无论是在相同的中继节点数量时，还是在相同的系统总功率约束下，本文提出的压缩转发系统的信噪比性能都要高于模拟中继转发系统。这说明当各个中继节点发射功率不同时，由中继节点对信源节点模拟信号进行压缩编码，要比直接放大转发有更高的信噪比增益，更能抵抗噪声干扰；或者，对于电池供电的系统，本系统可以在保证系统性能的情况下，能有效地延长服务寿命。另外，仿真结果也表明，当每个中继节点分配到的功率不同时，其性能要优于功率分配相同的情况。