基于ArcReLU函数的神经网络激活函数优化研究

许赟杰 徐菲菲

（上海电力学院计算机科学与技术学院，上海，200090）

引 言

深度学习的概念源于人工神经网络[1]的研究，而激活函数更是人工神经网络模型在理解和学习非线性函数时不可或缺的部分。若不使用激活函数，神经网络每一层的输出都是上一层输入的线性函数，无论神经网络具有多少层，输出皆为输入的线性组合，该类情况就是最基本的感知机。因此需要使用激活函数为神经元引入非线性因素，使神经网络可以任意逼近任何非线性函数，这样才能让神经网络应用到众多的非线性模型中。本文则基于误差反向传播神经网络，对常用激活函数进行研究对比，而后对其不足之处进行改进，以提高其最终的收敛速度和计算精度。在激活函数中最为常见的为Sigmoid系函数和ReLU系函数。

Sigmoid函数[2]在Sigmoid系函数中最具代表性，其具有软饱和性[3]，即该函数在定义域内处处可导，但当输入值过大或过小时，其斜率趋近于0，同时其导数也趋近于0，这将导致向底层传递时的梯度变得非常小。由于其在BP神经网络向下传导的梯度内包含了一个自身关于输入的导数因子，一旦输入落入饱和区之中，该因子将会接近于0，致使向底层传递的梯度变得极小，此时，神经网络的参数很难得到有效的训练，即会出现梯度消失[4]现象。这一现象使得BP网络一直难以得到有效的训练。同时，由于基本没有信号通过神经元传至权重再到输入值，这时梯度在模型更新中将难以起到作用。这也导致了无法对参数进行微调，随即影响到最终结果的精确值。这些也是阻碍神经网络进一步发展的重要原因。

Tanh函数[5]作为Sigmoid函数的一个变体，同样存在软饱和性的问题，但该函数以0点为中心，缓解了Sigmoid均值偏移的问题，同时提高了收敛速度。

经过学者们的研究，目前较为流行的神经网络的激活函数为修正线性单元(ReLU)[6]。它首先被用于限制玻尔兹曼机器，然后成功应用于神经网络。ReLU的导数在正轴部分恒为1，保持梯度不衰减，从而有效缓解了梯度消失的问题。该函数在反向传播过程中能够将梯度更好地传递给后层网络，同时计算速度更快。但其负轴部分会使其输入值落入硬饱和区，致使出现神经元死亡的情况，然而这一现象可以减少参数间的相互依存关系，继而缓解了过拟合问题的发生。另一方面，该函数也存在均值偏移的问题，即输出均值恒大于0。

指数线性单元（Exponential linear unit,ELU）[7]是ReLU的修正类激活函数。当输入值为负数时，ELU输出一个负值，这使得单元激活均值可以趋近于0，同时只需要更低的计算复杂度。ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。

本文通过对经典的Sigmoid系和ReLU系激活函数的研究与分析，提出与Sigmoid系激活函数同为S型图像的反正切函数(Arctan)，分析其在BP神经网络中应用的优点和不足之处。最终提出构想，通过结合ReLU函数和Arctan函数，构造出一种新型的激活函数ArcReLU。实验结果可以说明，一方面，ArcReLU函数相较于Sigmoid系和ReLU系函数具有更快的收敛速度并能有效地降低训练误差，同时还能有效缓解梯度消失的问题，解决ReLU函数具有的硬饱和性，进一步由于其负轴部分的导数趋于0的速度更慢，相较于Sigmoid系函数更为缓和，这一点使其负轴部分的饱和区间更为广泛，学习效率也会得到提高。另一方面，其导数的计算相较于另外两系的激活函数也将更为昂贵。

1 背景知识

1.1 ReLU函数

ReLU函数有效地解决了Sigmoid系函数在神经网络中梯度消失的问题，但从函数图(图1）中不难看出，该函数依旧存在均值偏移的问题。其定义如下

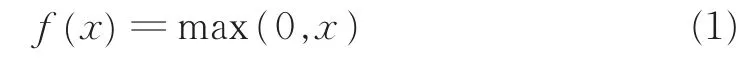
从函数图像及表达式中可以看出，当x≥0时，其导数值恒为1，因此，ReLU函数在x≥0时能够保持梯度不衰减，可以有效缓解梯度消失的问题。ReLU函数在反向传播过程中能够将梯度更好地传递给后层网络，同时计算速度较快。当x＜0时该函数具有硬饱和性[2]。如果此时有输入值落入该区域，则该神经元的梯度将永远为0，其对应权重也将无法更新，即出现神经元死亡的情况，致使计算结果不收敛。由于一部分的神经元输出为0，减少了参数间的相互依存关系，这也有效缓解了过拟合问题的发生。而ReLU函数在x＜0时输出为0，使得整体输出均值大于0，即存在均值偏移问题[6]，这也在一定程度上造成了神经网络的稀疏特性。

图1 ReLU函数图像Fig.1 Graph of function ReLU

1.2 Arctan函数

在图像上与Sigmoid系函数相类似的Arctan函数，输出范围在，其定义为

Arctan函数图像如图2所示。从表达式和图像中可以看出，Arctan函数具有软饱和性，即会使BP神经网络出现梯度消失的现象。相较于其他Sigmoid系函数，Arctan函数更为平缓，这使其比其他双曲线更为清晰，也意味着该函数没有Sigmoid和Tanh函数那么敏感，处于饱和度的区间范围比这两个函数更广。同时，其导数趋于0的速度更慢，这意味着学习效率更高，也能更好地缓解梯度消失的问题。然而，其导数的计算将比Tanh函数更加昂贵。

图2 Arctan函数图像Fig.2 Graph of function Arctan

2 基于ReLU函数的变体ArcReLU函数

基于对上述经典激活函数的研究及分析，结合ReLU函数以及Arctan函数的优点，为缓解ReLU函数神经元死亡的问题，降低Arctan函数的计算消费，结合两者构造出一种新的ArcReLU激活函数。将ReLU函数输入值小于0的部分替换为，在输入值大于0的部分使用ReLU函数。在使用Arctan函数时，为了限制其输出范围，将算子乘以，当网络进入一些比较大的输入值时也能保持稳定。其定义如下

ArcReLU函数图像如图3所示。由图像上可以初步推断，该函数在其定义域范围内可导且单调递增，只需要证明该函数在0点处的可导性。以下证明过程中将x＞0的部分称为f1(x)，x≤0的部分称为f2(x)，其证明如下

图3 ArcReLU函数Fig.3 Graph of function ArcReLU

式（4）说明ArcReLU在0点有定义且连续。由于式（5）与式（6）的结果存在且相等，依据导数定义，该函数在0点处可导。即可得出ArcReLU的导数如下

从式（7）可看出，ArcReLU函数的导函数值恒大于0。依据导数定义，可证明其为单调递增函数。当激活函数是单调的时候，单层网络能够保证为凸函数[8]。从而可以推断出该函数在训练过程中将会更容易收敛。

由于修正线性单元ReLU是分段线性的非饱和激活函数，相比于传统的S型激活函数，具有更快的随机梯度下降收敛速度，且计算简单。相比于Sigmoid系的激活函数，ReLU更具稀疏性。但过分的稀疏性也会带来更高的错误率并降低模型的有效容量。如此构造函数，不仅保留了ReLU函数计算简单的优点，还使得负轴的值也得以保存，不至于全部丢失。在负轴使用Arctan函数进行替代，不仅能够使得均值更趋向于0，缓解均值偏移问题，而且其左侧部分具备软饱和性，使其不会出现神经元死亡的现象，同时经过上述证明也使新构造的激活函数具备单调递增的特性，进一步提高其收敛速度。

3 实验与结果分析

3.1 实验数据

本文将分别在BP神经网络中使用ReLU函数，ELU函数和ArcReLU函数进行5次实验，所使用的数据为UCI上的数据集。实验通过Python3.6语言编写程序，在Windows 10操作系统下进行。5组数据集分别是关于皮马印第安人糖尿病的数据统计，文件大小为23.4 KB，共768个对象；鸢尾花的分类，文件大小为1.74 KB，共100个对象；汽车评估，文件大小为25.3 KB，共1 728个对象；美国人口普查收入，90.5 KB，共4 751个对象；阿维拉数据集，文件大小为1.14 MB，共12 495个对象。5组数据集的数据格式分别如表1—5所示。表1—5中最右侧的属性在实验中分别作为决策属性，取值均为0或1。

通过3种函数在5组不同数据集上的对比实验，能够清晰地看出各激活函数的优点与不足。本次实验使用10次10折交叉验证，在二层BP神经网络中进行测试。实验中学习率η经测试取值0.01，循环次数设置为5 000次。同时，考虑到BP神经网络存在局部最小点，因此在BP网络中加入了动量项，以此缓解局部最小点的出现并提高收敛速度。

表1 皮马印第安人糖尿病数据集Tab.1 Pima Indians diabetes data set

表2 鸢尾花数据集Tab.2 Iris data set

表3 汽车评估数据集Tab.3 Car evaluation data set

表4 美国人口普查收入数据集Tab.4 Adult data set

表5 阿维拉数据集Tab.5 Avila data set

鉴于不同的评价指标往往具有不同的量纲和量纲单位，将会影响到数据分析的结果。为了消除指标之间的量纲影响，在开始实验前对数据进行了z-score标准化的预处理，使指标的特征保持在相同范围内，以解决数据指标之间的可比性。为了直观地比较各激活函数之间的训练时间和误差率的差异，以下通过图表的形式将实验结果进行展示。

3.2 皮马印第安人糖尿病数据集实验结果

表6为3种函数在第1组数据集中的计算时间，从小到大的排序为ReLU＜ELU＜ArcReLU，由此可以得出在本次实验中ArcReLU的计算相较于另外两个函数稍为昂贵。图4显示了各激活函数在本次实验中的收敛速度。从图4可以看出实验过程中各函数的收敛速度从小到大排序为ReLU＜ELU＜ArcReLU，由此进一步验证前期理论证明的ArcReLU收敛速度高于另外两种函数。

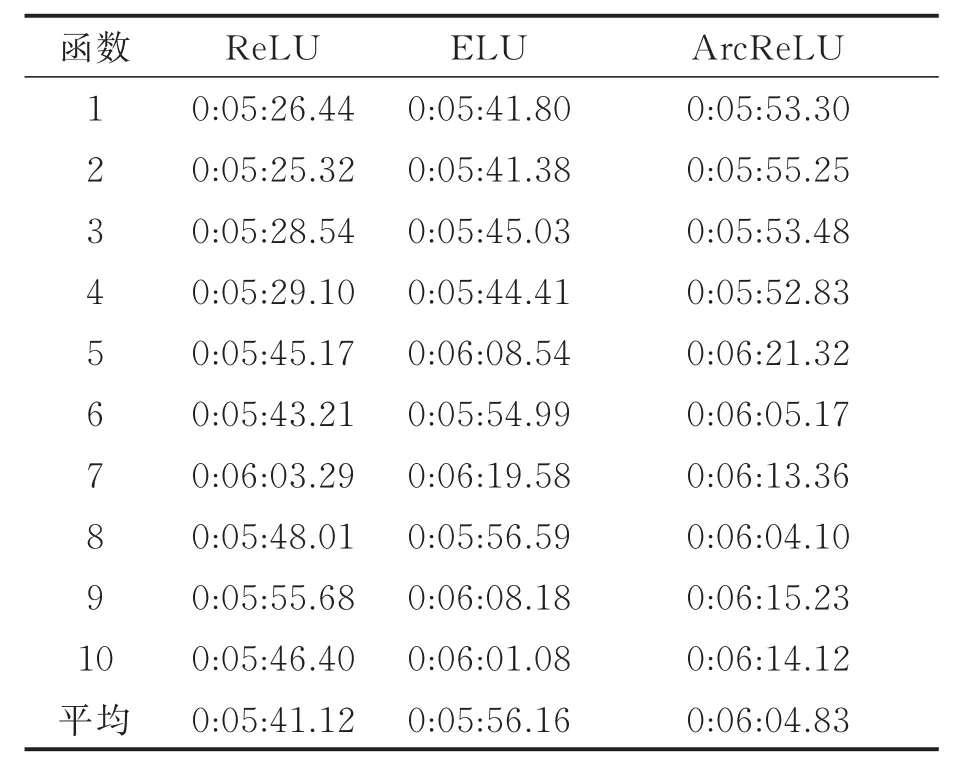
表6 第1组数据集中各激活函数计算时间Tab.6 Calculating time of each activation function in the first data set

图5是3种激活函数的受试者工作特性曲线ROC比较图，从图中较难看出这3种激活函数的优劣，因此需要通过求得ROC曲线下的面积值AUC进行比对。图中横坐标FPR表示将负例错分为正例的概率，纵坐标TPR表示将正例分对的概率。各函数AUC值及分类精度均值如表7，8所示。从表7，8可以看出ArcReLU函数的AUC面积以及分类精度均大于ReLU以及ELU，由此可以得出，在当前数据集中ArcReLU的分类效果优于另外两种函数。

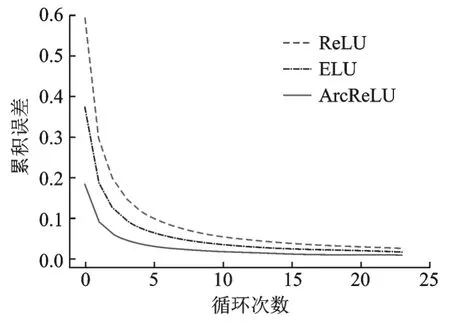
图4 第1组数据集中各激活函数收敛速度比较图Fig.4 Convergence rate comparison of each activation function in the first data set

图5 第1组数据集中各激活函数ROC比较图Fig.5 ROC comparison of each activation function in the first data set

表7 第1组数据集中各激活函数AUCTab.7 AUC comparison of each activation function in the first data set

表8 第1组数据集中各激活函数分类精度均值Tab.8 Mean classification accuracy of each activation function in the first data set %

3.3 鸢尾花数据集分类实验结果

表9为3种函数在第2组数据集中的计算时间，从小到大的排序为ReLU＜ELU＜ArcReLU，由此可以得出在本次实验中ArcReLU的计算相较于另外两个函数较为昂贵。图6显示了各激活函数在本次实验中的收敛速度。从图6可以看出实验过程中各函数的收敛速度从小到大排序为ReLU＜ELU＜ArcReLU，由此可以得出ArcReLU的收敛速度高于另外两种函数。

图7是3种激活函数的ROC比较图，从图中较难看出这3种激活函数的优劣，因此通过计算ROC曲线下的面积值AUC进行比对，各函数AUC及分类精度均值如表10，11所示。从表10，11可以看出ArcReLU函数的AUC面积以及分类精度均大于ReLU以及ELU，由此可以得出，在当前数据集中ArcReLU的分类效果优于另外两种函数。

表9 第2组数据集中各激活函数计算时间Tab.9 Calculating time of each activation function in the second data set

图6 第2组数据集中各激活函数收敛速度比较图Fig.6 Convergence rate comparison of each activation function in the second data set

图7 第2组数据集中各激活函数ROC比较图Fig.7 ROC comparison of each activation function in the second data set

3.4 汽车评估实验结果

表12为3种函数在第3组数据集中的计算时间，从小到大的排序为ReLU＜ELU＜ArcReLU，由此可以得出在本次实验中ArcReLU的计算相较于另外两个函数较为昂贵。图8显示了各激活函数在本次实验中的收敛速度。从图8可以看出实验过程中各函数的收敛速度从小到大排序为ReLU＜ELU＜ArcReLU，由此可以得出ArcReLU的收敛速度高于另外两种函数。

图9是3种激活函数的ROC比较图，从图中较难看出这3种激活函数的优劣，因此通过计算ROC曲线下的面积值AUC进行比对得出结论。各函数AUC及分类精度均值如表13，14所示。从表13，14可以看出ArcReLU函数的AUC面积以及分类精度均大于ReLU以及ELU，由此可以得出，在当前数据集中ArcReLU的分类效果优于另外两种函数。

表10 第2组数据集中各激活函数AUCTab.10 AUC comparison of each activation function in the second data set

表11 第2组数据集中各激活函数分类精度均值Tab.11 Mean classification accuracy of each activation function in the second data set %

表12 第3组数据集中各激活函数计算时间Tab.12 Calculating time of each activation function in the third data set

3.5 美国人口普查收入实验结果

表15为3种函数在第4组数据集中的计算时间，从小到大的排序为ReLU＜ArcReLU＜ELU，由此可以得出在本次实验中ELU的计算相较于另外两个函数较为昂贵。

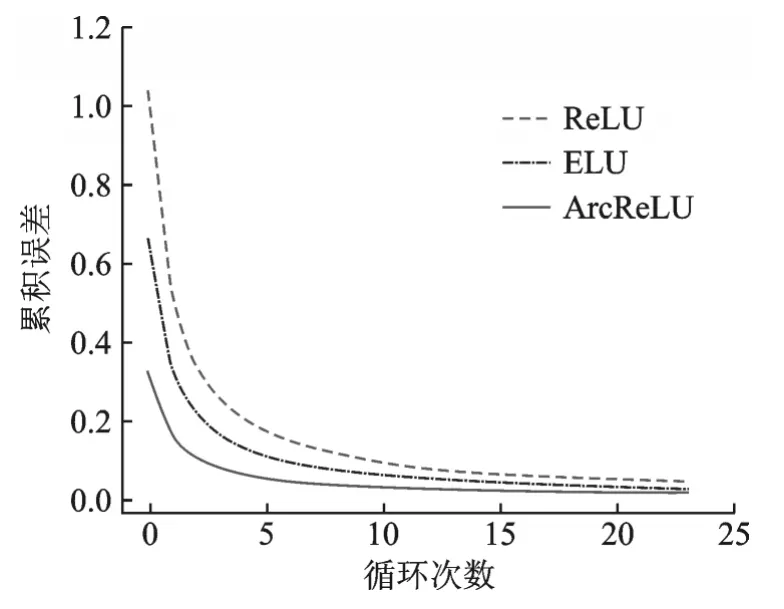
图8 第3组数据集中各激活函数收敛速度比较图Fig.8 Convergence rate comparison of each activation function in the third data set

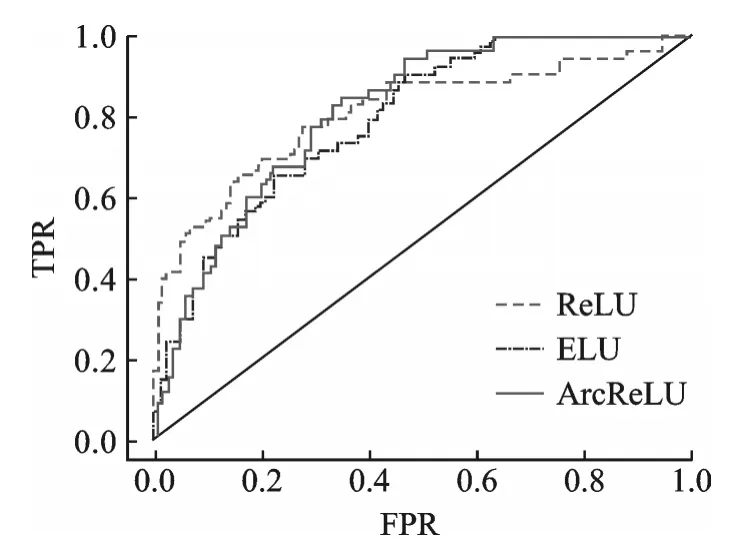
图9 第3组数据集中各激活函数ROC比较图Fig.9 ROC comparison of each activation function in the third data set

表13 第3组数据集中各激活函数AUCTab.13 AUC comparison of each activation function in the third data set

表14 第3组数据集中各激活函数分类精度均值Tab.14 Mean classification accuracy of each activation function in the third data set %

这一结果与前3组的结果有所不同。由于每组实验都是在相同的运行环境下计算的，从以上实验结果看，ELU适合数据量较小的计算，ArcReLU适合数据量大的计算。为了确认随着数据量的增减是否对ReLU函数的计算时间有影响，在3.6节中分别计算了5组实验中，ArcReLU相较于ELU的计算时间增量和ArcReLU相较于ReLU的计算时间增量，结果如表16所示。图10显示了各激活函数在本次实验中的收敛速度。从图10可以看出实验过程中各函数的收敛速度从小到大排序为ReLU＜ELU＜ArcReLU，由此可以得出ArcReLU的收敛速度高于另外两种函数。

图11是3种激活函数的ROC比较图，从图中较难看出这3种激活函数的优劣，因此通过计算ROC曲线下的面积值AUC进行比对得出结论。各函数AUC和分类精度均值如表17，18所示。从表17，18可以看出ArcReLU函数的AUC面积以及分类精度均大于ReLU以及ELU，由此可以得出，在当前数据集中ArcReLU的分类效果优于另外两种函数。

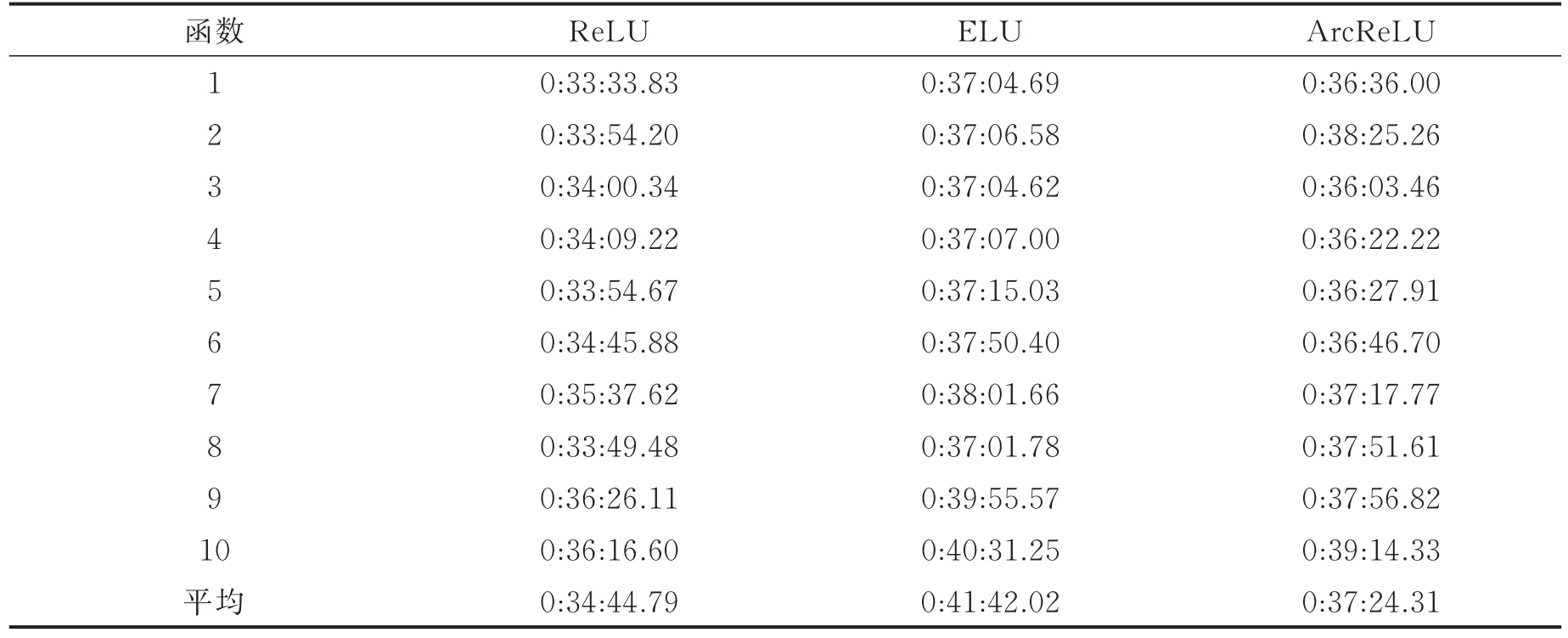
表15 第4组数据集中各激活函数计算时间Tab.15 Calculating time of each activation function in the fourth data set

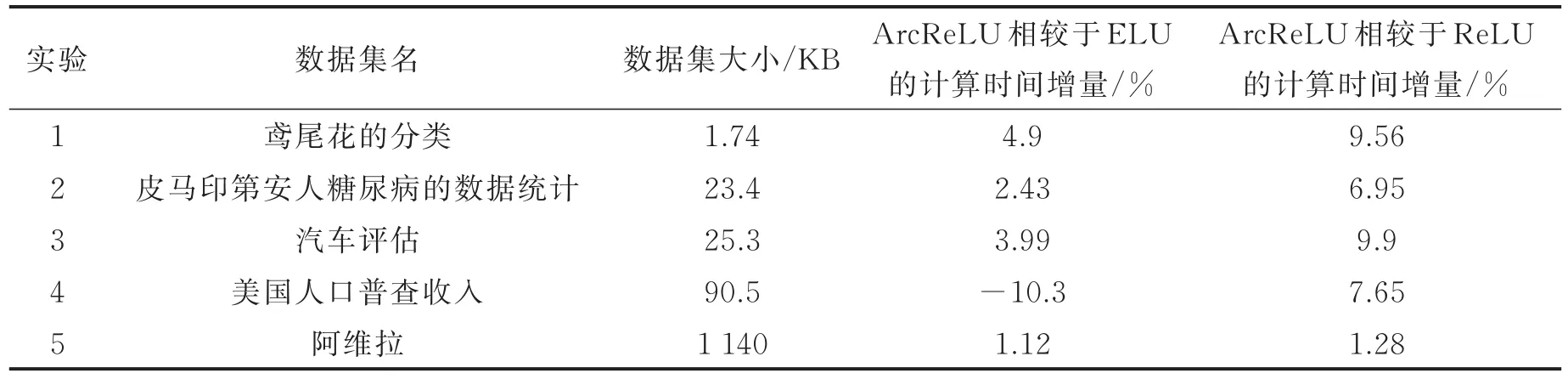
表16 各激活函数间计算时间增量的比较Tab.16 Comparisons of calculating time increments among activation functions

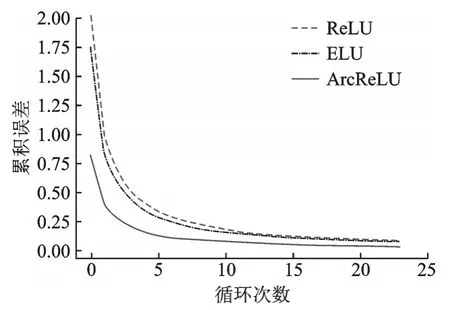
图10 第4组数据集中各激活函数收敛速度比较Fig.10 Convergence rate comparison of each activation function in the fourth data set

3.6 阿维拉实验结果

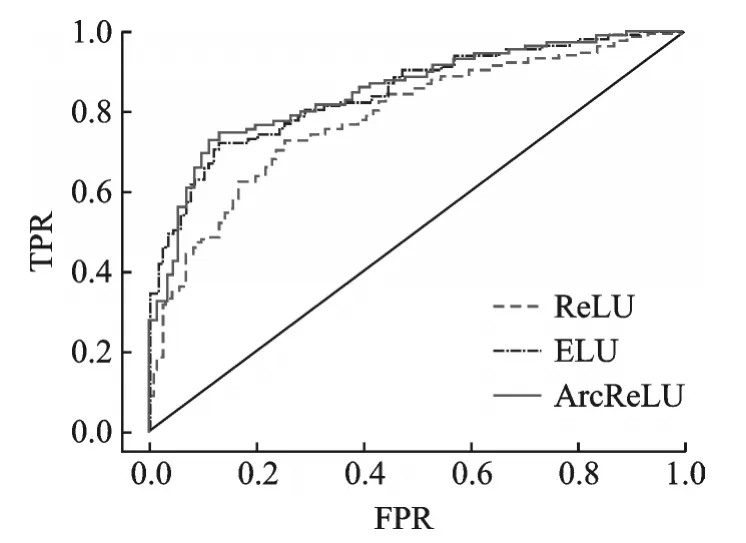
图11 第4组数据集中各激活函数ROC比较Fig.11 ROC comparison of each activation function in the fourth data set

表19为3种函数在第5组数据集中的计算耗时，从小到大的排序为ReLU＜ELU＜ArcReLU，由此可以得出在本次实验中ArcReLU的计算相较于另外两个函数较为昂贵。由于5组实验数据中第4组的实验结果较为不同，此处分别计算了5组实验中，ArcReLU相较于ELU的计算时间增量和ArcReLU相较于ReLU的计算时间增量，见表16。

表17 第4组数据集中各激活函数AUCTab.17 AUC comparison of each activation function in the fourth data set

表18 第4组数据集中各激活函数分类精度均值Tab.18 Mean classification accuracy of each activation function in the fourth data set %

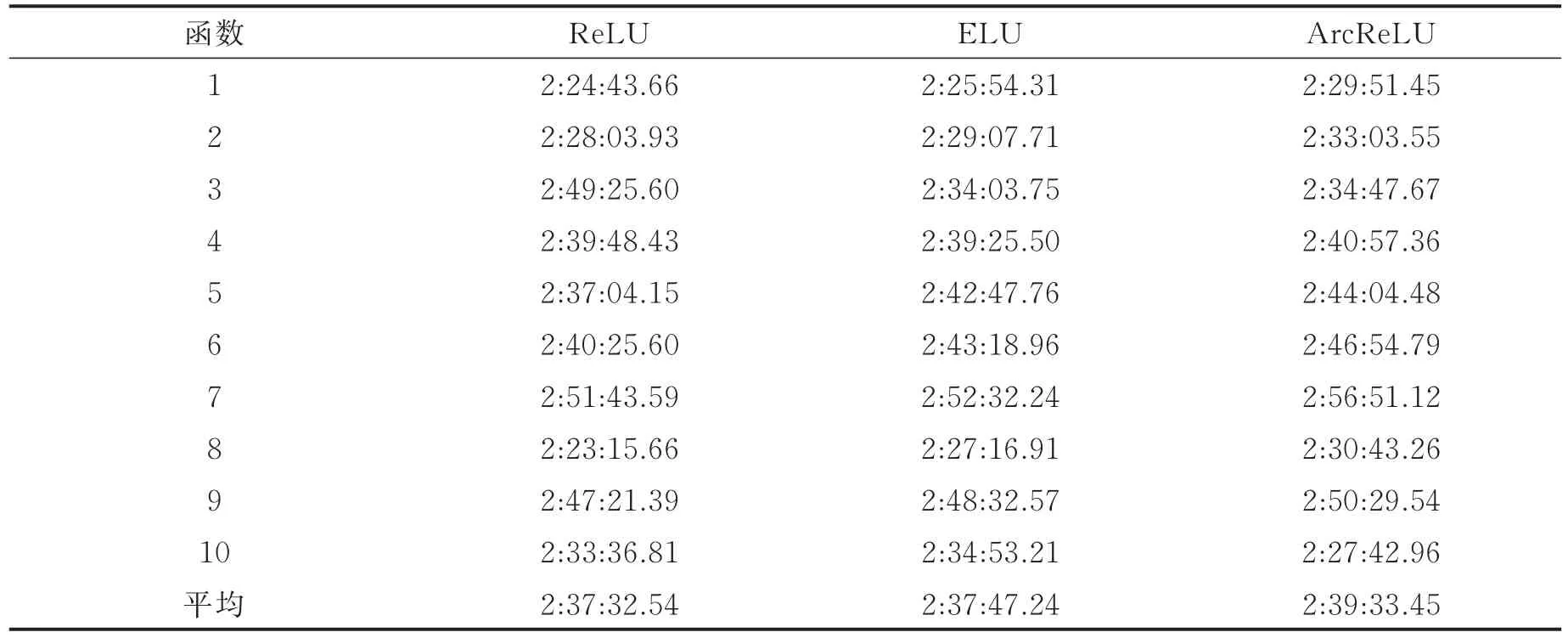
表19 第5组数据集中各激活函数计算时间Tab.19 Calculating time of each activation function in the fifth data set

基于表6，9，12，15和表19中的各激活函数计算时间，可以得出结论，随着数据集的增大，ArcReLU所需的计算时间也会增加，同时从实验结果可以看出三者之间的时间增量在逐步缩小。在后续的研究工作中，将添加更多不同的数据集，对相同的数据集反复进行计算，排除单次实验的特殊性，从而进行进一步的研究。

图12显示了各激活函数在本次实验中的收敛速度。从图12可以看出实验过程中各函数的收敛速度从小到大排序为ReLU＜ELU＜ArcReLU，由此可以得出ArcReLU的收敛速度高于另外两种函数。

图13是3种激活函数的ROC比较图，从图中较难看出这3种激活函数的优劣，因此通过计算ROC曲线下的面积值AUC，进行比对得出结论。各函数AUC和分类精度均值如表20，21所示。从表20，21可以看出ArcReLU函数的AUC面积以及分类精度均大于ReLU以及ELU，由此可以得出，在当前数据集中ArcReLU的分类效果优于另外两种函数。

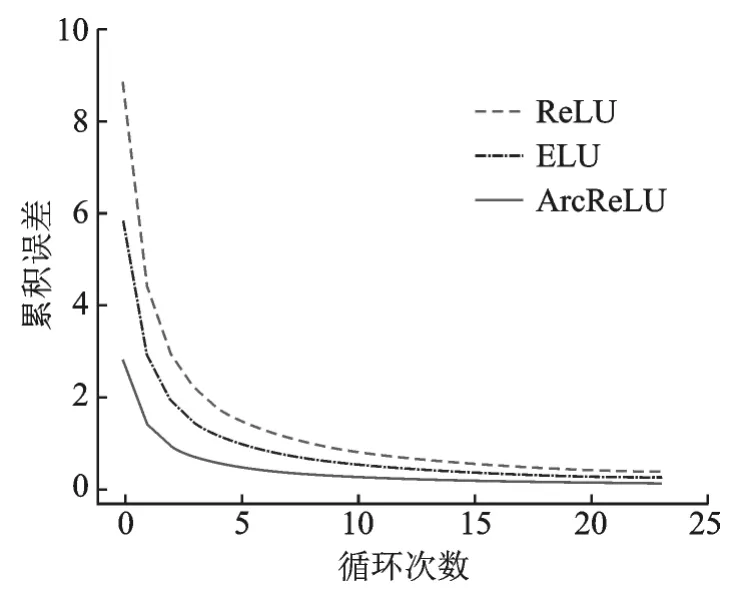
图12 第5组数据集中各激活函数收敛速度比较Fig.12 Convergence rate comparison of each activation function in the fifth data set

图13 第5组数据集中各激活函数ROC比较Fig.13 ROC comparison of each activation function in the fifth data set

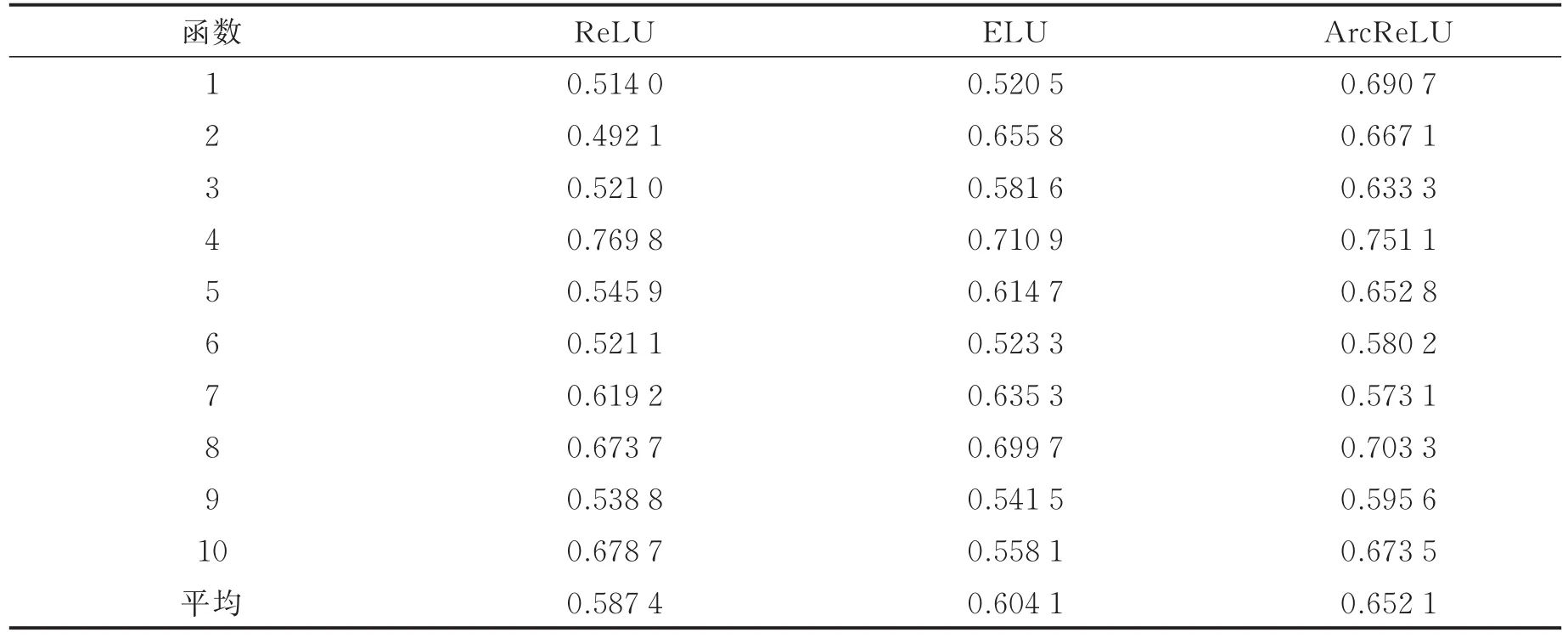
表20 第5组数据集中各激活函数AUCTab.20 AUC comparison of each activation function in the fifth data set

表21 第5组数据集中各激活函数分类精度均值Tab.21 Mean classification accuracy of each activation function in the fifth data set %

从上述5组实验结果可以看出，虽然ArcReLU的计算时间略多于ReLU和ELU两个函数，但5次实验结果均说明其收敛速度、分类精度以及AUC面积高于其他两种激活函数。同时也验证了Arctan函数由于导数趋于0的速度更为缓慢，因此当输入值落入负轴时，ArcReLU函数的收敛速度高于另外两个激活函数，即该函数可以有效地减少训练误差。

4 结束语

本文通过分析研究经典的激活函数，结合Arctan函数的性质，构造出一种新的激活函数ArcReLU。随后，通过5组不同的数据集，分别将该函数与两种较为常用的ReLU系激活函数进行对比实验。从结果可以看出，ArcReLU函数相较于另外两个函数，初始的累积误差小，具有较快的收敛速度。伴随着迭代次数的增加，ArcReLU函数将更快趋于平稳，进一步说明它具有较好的收敛性并能有效地降低训练误差。同时，结合ReLU系函数的特性，ArcReLU函数能够有效缓解梯度消失的问题。负轴部分为Arctan函数，可以缓解ReLU函数的硬饱和性，进一步由于Arctan函数更为缓和，使得负轴的饱和区间范围相较于Sigmoid系函数更为广泛。在实验中也能够看出，ArcReLU的AUC值比另外两个函数大，由此可见，ArcReLU的泛化性能优于另外两种函数。

另外，由于ArcReLU函数负轴部分为Arctan函数，三角函数在计算机中的运算复杂度相当于乘除法，而另外两种激活函数的运算复杂度仅相当于加法运算。因此理论上ArcReLU函数在计算消耗方面会略大于另外两个激活函数，所需的计算时间也就略长。通过5组实验结果可以得出，随着数据量的增加，ArcReLU的计算消耗也略为昂贵。下一步研究工作将对于ArcReLU的鲁棒性进行探讨，从而确认其是否适用于无监督学习、多种分类结果的监督学习或深度学习。另外，还会对其计算时间与数据集大小的关联性进行研究，通过添加不同的数据集，反复进行实验，从而确认其是否有所关联。