基于B样条二进小波变换的故障选相研究

(国网天津滨海供电公司，天津 300450)

0 引 言

当输电线路发生故障后，在故障电气量中会包含一种频率很高的暂态量信号，该信号被称为行波信号，其包含了与故障情况相关的丰富信息。正确地从行波信号中识别和提取与故障相关的信息可以为快速准确地识别故障相、选择性地切除故障相提供依据。在继电保护现有工程实际和研究中，为了保证选相的快速性，故障选相方法采用行波信号的特征直接构成判别方法。目前对于采用行波信号进行故障相别判别的方法主要包括以下几种：1)采用行波方向判别方法作为故障相别判别的方法，当根据方向判别方法判断某相为正方向时，该相即判断为故障相。这种选相判别方法在RALDA型行波保护中[1]得到了应用。2)基于各相电流行波峰值进行故障选相的方法，通过比较检测期间三相行波电流故障分量峰值与电流最大的一相的故障分量最大值进行故障相判别。当任意一相电流的最大值大于电流最大一相的故障分量最大值的1/2时，判断该相为故障相。这种选相方法是对选相方法1)的改进，在工程实践中已经有应用[2]。3)基于电流行波比较原理的选相方法，通过比较三相行波电流之差(IA-IB，IB-IC，IC-IA)的极性进行判别。当两两之间的极性相反时，相邻元件输出正值并判定为故障相[2]。

上述方法通过利用故障时行波信号中的暂态量信息，为故障时选相提供了思路，但在选相正确性方面仍存在一些问题。其中，方法1)和方法2)利用行波方向判别方法进行选相，无法避免因不同相间的电磁耦合引起的选相不正确问题。同时，与方法3)一样，由于选相元件采用故障时行波瞬时值的特征进行故障相选择，而瞬时值受波形畸变、瞬变干扰的影响较大，容易造成分析结果的不可靠。此外，由于故障发生地点具有随机不可控的特性，这将造成行波波头在瞬时采样过程中采样值的数目不易确定。

小波变换因其在信号处理过程中具有使信号时频特性局部化的优点，近年来在数学和数字信号处理领域得到了充分的应用和发展[3-5]。在电力行业应用方面，小波变换被广泛应用于行波信号的分析。这里的基本出发点是充分利用小波变换在暂态信号处理上的优点，避免选相受电磁耦合、波形畸变、瞬变等干扰的影响。考虑到行波信号在到达测量点时的突变性质以及小波变换具有将行波信号的特征进行时频局部化的作用[6-7]，因此结合行波信号和B样条二进小波变换，对电流行波信号进行时频分析，通过模故障分量构成更完善、更快速、更准确的故障选相方法。首先对B样条二进小波的优点进行分析，然后运用B样条二进小波对解耦变换后的模电流分量进行分析，计算得到模电流分量初始行波的模极大值，并根据模电流分量极大值在不同故障类型下的不同特征进行对比分析从而构建出故障选相原理。最后，通过仿真验证选相原理的正确性。

1 B样条小波及其优点

在小波分析中，由于B样条小波具有优良的光滑性和紧支撑性，因此，在现代行波故障分析中一般使用B样条函数的导函数作为基小波函数。B样条函数是一种半正定的、分段光滑的函数，m次B样条函数的表达式为

βm(x)=βm-1(x)·β0(x)，m≥1

(1)

其中：

(2)

由表达式可知B样条函数是分段多项式，这使得其处理非常简化。此外B样条函数具有对称性，可以由它构造出对称或反对称的样条小波，且可以达到非常高的近似精度。

以B样条函数构造的二进小波变换具有平移不变性，使信号奇异点的检测变得简单。当行波到达信号测量点时，测量点将测得一发生“突变”的信号，对该信号进行小波变换，即可获得对应于信号突变的模极大值。因此，借助B样条二进小波变换即可将行波信号的分析转化为其小波变换下的模极大值的分析，从而使基于行波信号的故障选相简单易行。

根据已有文献的分析结论有：三次B样条函数对提取含噪声信号的奇异性是渐进最优的。因此，采用三次样条函数作为二进小波变换的基函数，其对应表达式为

(3)

对故障时的行波信号进行三次B样条二进小波变换即可获得故障时行波信号特征。

2 故障电流的解耦变换与小波变换

当输电线路上发生故障时，可运用小波变换对量测点的信号进行处理得到该信号的模极大值，通过模极大值即可对该信号进行表征。运用模极大值的表征作用即可通过工频电流信号的分析实现基于模故障分量的故障选相，从而将工频量信号应用于行波选相中，实现仅通过故障时电流的初始行波判断故障相别的目的。

由于三相输电线路中各相电流不独立，因此无法完全消除非故障相对故障相电流的影响，需要通过解耦变换得到独立的模电流分量进行故障选相。以下假定在故障发生后母线流向故障点的三相故障电流分别为IA、IB、IC，计算在不同类型故障条件下的母线流向故障点的行波电流。运用相模变换对三相故障电流进行解耦变换与分析，建立非独立的三相电流与解耦的模电流之间的数量关系。相模变换可采用的变换方法主要包括Karenbauer变换、Clarke变换等几种常用的解耦变换方法。以Karenbauer变换为例建立故障后三相电流的模电流分量，Karenbauer变换因子的表达式为

(4)

利用上述Karenbauer变换因子对故障电流进行变换可得三相故障电流与各模电流的关系如下：

(5)

式中：零模电流分量I0通过大地和导线构成电流回路，该回路的波阻抗相对较大，波传播的速度相对较小，传播过程中的衰耗相对较大；线模电流分量Iα、Iβ通过导线构成电流回路，该回路的波阻抗相对较小，波传播的速度与光速基本接近，且比较稳定，传播过程中的衰耗相对较小。为便于故障选相，引入“γ模”：

(6)

γ模不是独立的，它由α模和β模的线性组合而得到。需要注意的是，γ模的定义是建立在三相平衡系统上的。根据式(5)、式(6)和故障边界条件可以分别得到对应于接地型短路、非接地型短路和三相短路时各电流模量的情况，如表1所示。

在获得解耦的各模量电流后即可进行B样条二进小波变换，对故障后的模量电流进行特性分析。

3 故障特征分析及选相原理

根据上述分析可以得到发生不同类型故障及不同相故障时的故障电流模分量的特征。

1)故障情况下的零模分量

在无干扰的情况下，如果线路发生接地故障，此时的零模分量I0不等于0，而如果发生的故障为相间或者三相短路时零模分量I0等于0。因而可以根据零模电流的大小判断故障为接地故障还是相间或三相短路。

2)各种情况下的线模分量

两相相间短路时，线模电流满足关系式max(|3Iα|，|3Iβ|，|3Iγ|)=2min(|3Iα|，|3Iβ|，|3Iγ|)，再根据最大模量电流及对应线模电流可以确定故障相。

单相短路时，3个线模电流中有1个为0，其他2个线模电流相等。根据模量电流为0的线模电流可以确定故障相。

两相接地故障时，零模电流与线模电流存在3种情况：当满足I0=Iβ+Iγ时，两相接地故障的故障相为AB相；当满足I0=Iα-Iγ时，两相接地故障的故障相为CA相；当满足I0=-Iβ-Iα时，两相接地故障的故障相为BC相。

综上，基于B样条二进小波变换模极大值的故障相判别原理及其过程可总结为：通过三相电流计算得到故障情况下各个模量电流初始行波的B样条二进小波模极大值；通过电流模量中零模电流的小波模极大值与0的大小关系判断是否为接地故障，不为0时为接地故障，否则为非接地故障；通过电流模量中线模分量的关系可以判断故障时的相别。

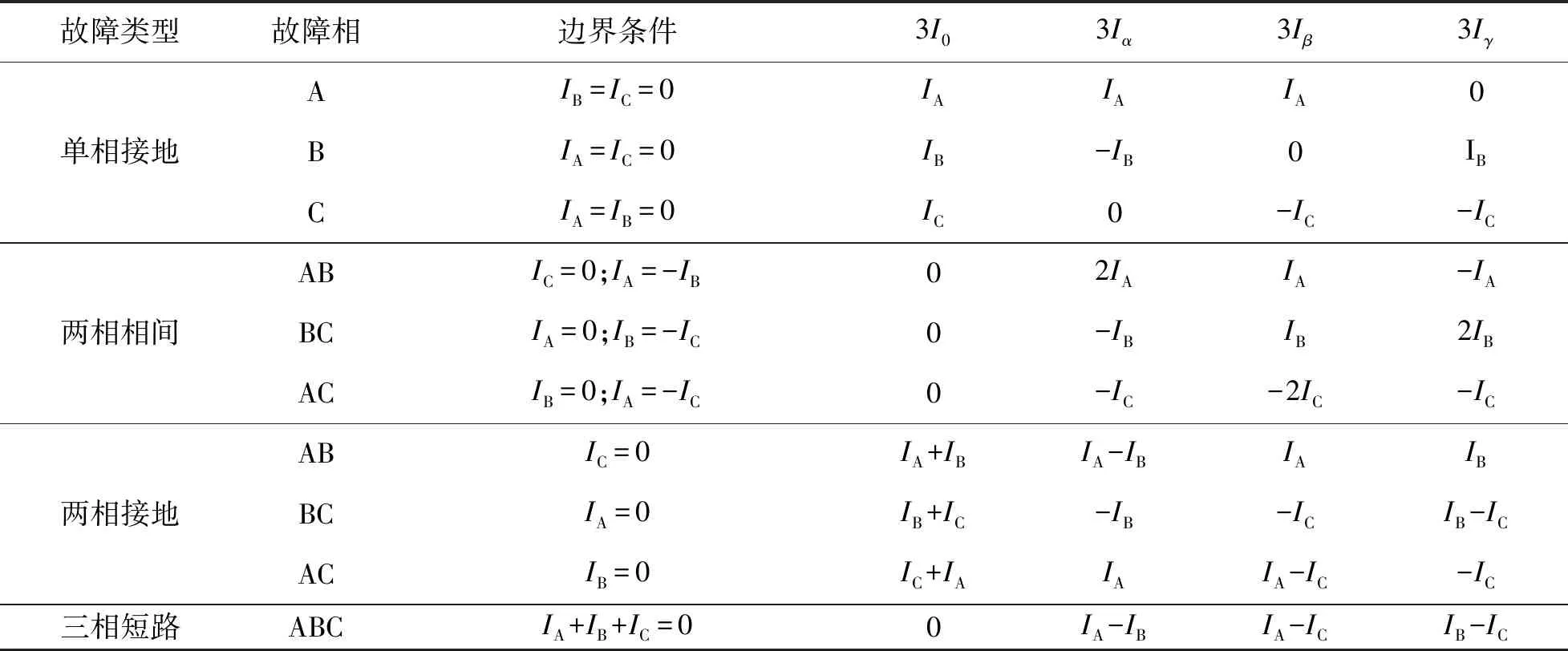
表1 不同故障类型和故障相下的模量电流

故障类型、故障相与零模、线模电流的对应关系如式(7)、式(8)、式(9)所示。

(7)

(8)

(9)

不满足上述3种条件者，判为三相故障。故障类型的判别与选相过程如图1所示。

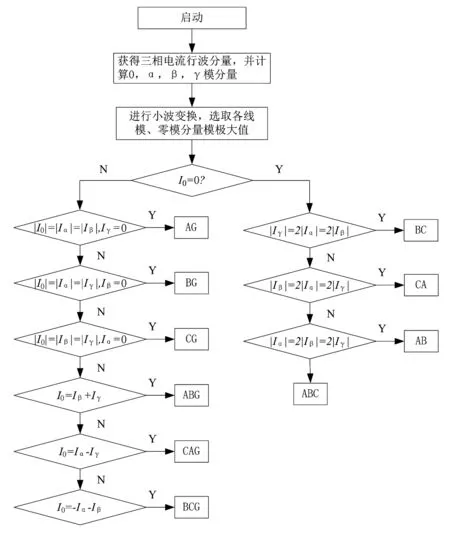
图1 故障类型判别与选相流程

理论上可以根据上述等式条件准确判别出故障类型及故障相，然而实际信号的提取和处理过程中存在各种误差和近似，因而需将上述判别故障类型和故障相的等式条件变为不等式条件，即当等式两边的差值在一定的误差范围内即认为等式成立，从而可在实际工程中实现上述判别方法。

4 仿真验证

为了验证了上述故障选相方法在不同故障类型和故障相别情况下的准确性和优越性，针对图2所示的仿真系统，采用PSCAD软件对其进行分析，获得系统故障时测量端处的暂态电流行波信号。并将PSCAD中获得的数据导入Matlab中进行数据处理，根据处理后的结果进行故障选相。数据处理采用基于三次B样条的小波函数进行小波变换，获得所需各个模量的模极大值。

图2 仿真系统

仿真中每隔0.000 002 s取一个点，即采样频率为0.5 MHz。以A相接地短路为例，故障发生在距离M侧母线90 km处，过渡电阻为0.01 Ω。保护安装处获得的A相接地短路电流及其模电流、小波变换结果如图3所示(故障发生在第1096个采样点处)。根据零模电流不为0，可知故障类型为接地故障，又由于I0≈Iα≈Iβ，Iγ≈0，对比表1和式(7)可知该故障类型为单相接地短路，故障相为A相。

同样地，利用B样条小波变换对其他单相接地短路、相间短路、相间接地短路和三相短路进行分析，可以得到对应不同故障类型下的零模电流和线模电流的小波模极大值如表2所示。对比表1和式(7)、式(8)、式(9)的故障模量特征即可由模电流的小波模极大值判断故障类型。

5 结 语

基于B样条二进小波变换，提出了一种根据暂态行波信号特征进行故障相别判断的方法，该方法利用模电流极大值数据进行故障相别判别，充分显示了选相时故障特征量的显著性，使选相的物理概念更加清晰；故障选相判据执行流程简单，选相逻辑清晰、速度快、可靠性高。该选相方法对故障点的过渡电阻、故障前的负荷电流、系统阻抗等因素具有很强的鲁棒性。此外，由于选相过程中合理利用了故障电流中的零模分量，使该方法在接地故障电流波形严重畸变的情况下也能够正确选相，克服了现有故障选相判别方法因相间电磁耦合作用造成选相错误的问题。

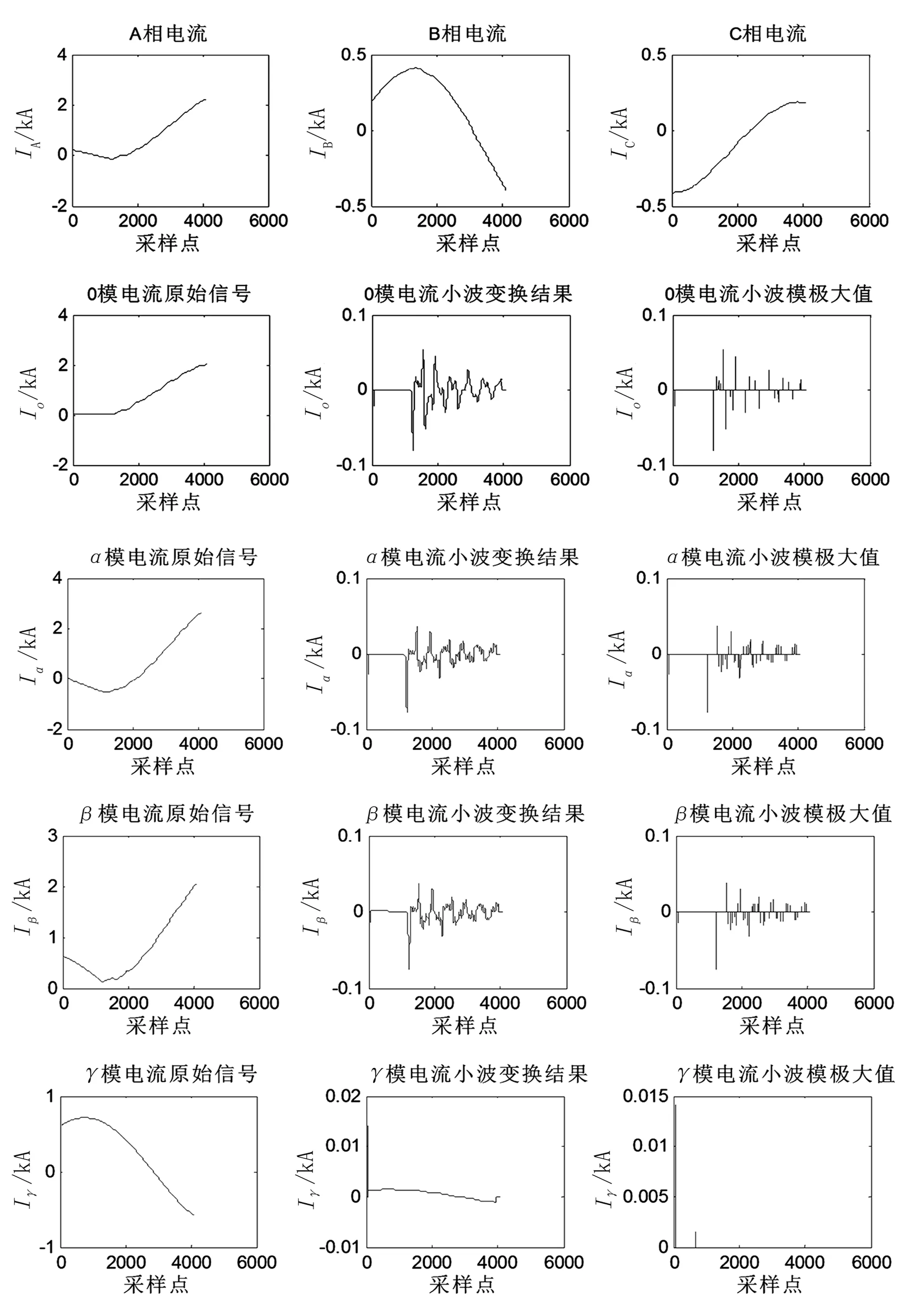
图3 A相故障电流及各模电流小波变换结果

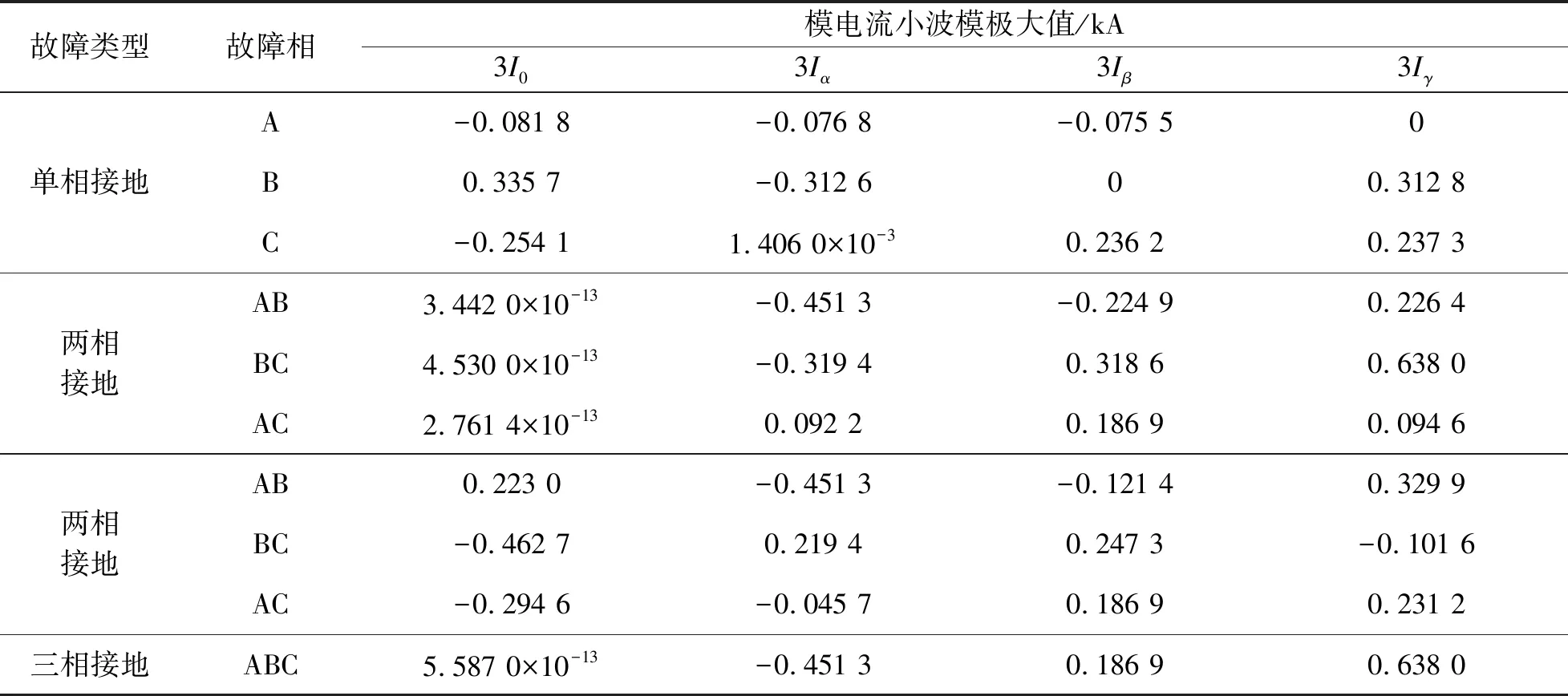
故障类型故障相模电流小波模极大值/kA3I03Iα3Iβ3Iγ单相接地A-0.081 8-0.076 8-0.075 50B0.335 7-0.312 600.312 8C-0.254 11.406 0×10-30.236 20.237 3两相接地AB3.442 0×10-13-0.451 3-0.224 90.226 4BC4.530 0×10-13-0.319 40.318 60.638 0AC2.761 4×10-130.092 20.186 90.094 6两相接地AB0.223 0-0.451 3-0.121 40.329 9BC-0.462 70.219 40.247 3-0.101 6AC-0.294 6-0.045 70.186 90.231 2三相接地ABC5.587 0×10-13-0.451 30.186 90.638 0