小水电站流域径流量的评估方法

曾思明，吴杰康2，陈永进，赵俊浩2，翁兴航

(1.广东电网有限责任公司韶关供电局，广东 韶关 512000； 2.广东工业大学自动化学院，广东 广州 510006)

0 引 言

韶关市地理位置是在广东省的中北部，由于地处温带而且受湿润的季风气候影响[1]，所以全年降水量充足，而且河流数目非常多，水量以及水力资源都十分丰富，非常有利于小水电的开发与建造。

其中，南水河作为韶关主要河流之一，其集水面积是1489 km2，多年的平均年径流量是1.34×109m3，由于南水河地貌的特点为峡谷非常多、河流落差较大，所以流域内已经建造了中大型的水库[2]。因此，如果能对南水河的径流量进行研究以及准确的预测，对于合理利用南水河的水资源有着重要的意义，也为开发小水电提供重要的科学依据。

近年来，许多学者已经使用了多种预测方法对径流量进行了预测与研究[3-6]。例如针对流溪河水库，文献[7]使用BP神经网络方法预测该水库的径流量。文献[8]以石泉水库为例，研究了BP神经网络以及马尔科夫预测的优劣，提出了BP神经网络马尔科夫模型来预测河流径流量。文献[9]采用灰色系统理论中的GM(1,1)模型，研究了黄河年径流量的变化特点，拟合并预测了唐乃亥河花园口的年径流量。在此基础上，文献[10]结合了R/S分析，采用R/S灰色预测的方法对黑河出山年径流量进行预测。文献[11]使用了支持向量机预测模型，以黄河上游兰州站为例，预测该水文站的年径流量。文献[12]则在支持向量机的基础上作出了改进，将改进后的模型应用在开都河年径流量的预测上。综合上述学者的研究，现在用于径流量的预测基本是利用多年的径流量数据作为模型的输入输出，利用各种算法找到输入输出之间的数学关系，以此来拟合并预测河流的径流量。

由于不同预测模型都有自己不一样的特点，如何在某一地点选择恰当的预测模型成为评估该地区水资源的一个难点。下面首先分析了灰色系统预测、基于遗传算法神经网络以及支持向量机3种预测方法对韶关市南水河径流量预测结果；然后对比3种方法的预测值与实际值的误差；最后评价各模型的性能，为研究南水河区域水资源以及评估该区域水资源丰富度提供科学的决策依据，对于在该区域研究以及建立微电网有着重要的意义。

1 径流量预测方法

由于韶关市南水河的径流量数据较少，而且该河流径流量的随机性以及波动性较大，为了更好研究韶关水资源的变化趋势，在预测方法中，采用了灰色系统理论中的GM(1,1)模型、基于遗传算法的BP神经网络以及支持向量机3种方法对南水河的年径流量进行拟合以及预测。

1.1 灰色预测

在传统的系统行为分析中，大多数的数据分析法都是要通过分析大量的历史数据，从中得到数据相关的数学规律。但是对于径流量这一物理量来说，其变化一般是随机波动的且历史数据量难以获取。而在灰色系统中，其预测方法是可以从少量的数据寻找系统的变化规律，并且灰色预测方法计算较为简单，所以首先使用灰色系统理论中的GM(1,1)模型[13-15]，并在此模型基础上作出改进用于径流量的预测。

1.1.1 GM(1,1)模型

GM(1,1)模型所对应的白化形式微分方程为

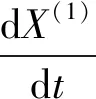
(1)

(2)

(3)

(4)

求解模型的微分方程，可以得到径流量的预测模型方程为

k=0,1,2,...,n

(5)

1.1.2 改进GM(1,1)模型

由于GM(1,1)模型只能应用于一阶线性微分方程，但是南水河的年径流量的变化是不符合这一条件的，直接使用GM(1,1)模型对南水河的年径流量进行预测是很难得到一个理想结果的，需对GM(1,1)模型进行改进。具体步骤如下：

1)在坐标轴上绘出南水河年径流量的逐年变化曲线图；

(6)

3)作阈值L与曲线的交点图，可以得到递增的时间序列；

4)将GM(1,1)模型用在该时间序列中，得到该阈值的预测模型；

5)作出其他阈值的GM(1,1)预测模型；

6)根据上述得到的一系列预测模型，作出径流量的预测图。

1.2 基于遗传算法的BP神经网络

由于BP神经网络在全局中的搜索能力差，比较容易陷入局部极值且算法的收敛速度较慢，当BP神经网络的权值和阈值选择不恰当的时候，网络输出的结果不理想，模拟精度较低，误差较大。所以针对径流量的预测，利用遗传算法在全局搜索能力强且速度较快的优点，将BP神经网络的权值和阈值放进遗传算法中进行优化，以BP神经网络输出的径流量预测值与实际值的误差作为遗传算法的适应度函数，得出最优的权值阈值。最后使用BP神经网络在这一组权值和阈值中进行仿真，得到最后的径流量预测输出值[16-20]。该优化模型的具体步骤如图1所示。

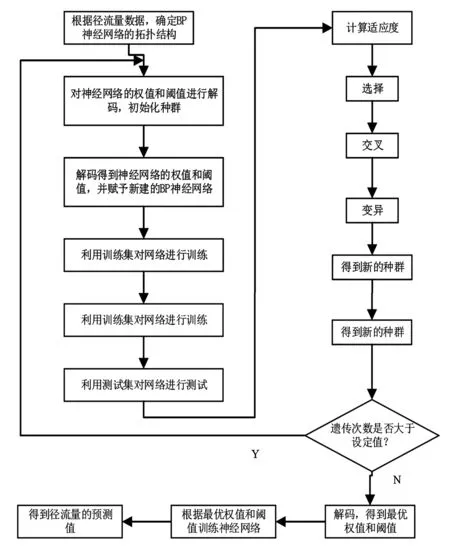
图1 基于遗传算法的BP神经网络流程

1.3 支持向量机

在统计学习的理论当中，认为当经验风险函数最小的时候，模型对于训练集的学习是最好的。但是这存在着约束条件，训练样本的数目需要足够大，这样经验风险最小化的模型才能够更好地进行学习。当训练样本较少的时候，根据这一经验风险最小化的理论来对模型进行训练则会出现过拟合。1995年，Corinna Cortes和Vapnik两位学者首次提出了支持向量机这一概念，这是基于上述统计学习理论所提出的一种新的算法。他们认为当某一数据集遵循某一规律分布的时候，如果要使得模型的实际输出值能更好地模拟实际值，就要使得结构风险最小化，而不是经验风险最小化。而支持向量机(support vector machine,SVM)则能很好地实现这一结构风险最小化的理论，在小样本的条件下，支持向量机可以在统计学习中的分类和回归的研究中起到非常理想的效果[21-25]。

支持向量机回归(support vector regression，SVR)是使用核函数将样本数据从地位空间映射到高维空间，然后在这个高维空间求解问题的回归方程。SVR对于径流量的预测回归步骤如下：

1)利用多年的径流量数据，径流量的回归预测函数在高维空间的形式为

f(x)=ωx+b

(7)

式中：ω是权值向量；b为偏置量。

2)若样本数据点在超平面与支持向量之间，则认为该数据点没有损失，定义如下：

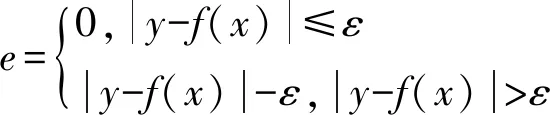
(8)

式中：y为实际的径流量；ε为反应允许偏差的参数。

3)引入松弛系数，则径流量回归问题可以表示为

(9)

(10)

4)根据拉格朗日乘子，将径流量回归问题变成对偶形式：

(11)

(12)

5)最后求解可得径流量回归预测函数为

表1 南水河年径流量预测模型

(13)

2 实验分析

为了对比上述3种方法对于径流量预测的结果，以韶关市的南水河为研究对象，利用Matlab软件[26-28]分别使用灰色预测、基于遗传算法的BP神经网络以及支持向量机对南水河1978—2015的年径流量进行仿真研究。

2.1 灰色预测结果

由于根据南水河1978—2010年径流量的数据，该河域在这33年最大流量为1.451×109m3，最小流量为5.35×108m3，所以使用灰色预测时，在设定阈值时，从最小值开始每次往上增加0.5×108m3，直到最大值，且当某些年份没有相对应的阈值，则设定该年份实际值也作为一个阈值，要求每个阈值对应的样本数不少于4个，因此对于南水河一共建立了14个模型，结果如表1所示。

图2是灰色预测对南水河径流量的拟合值与实际径流量的对比，可以看出拟合出来的曲线大部分年份的拟合值与实际值相差不大，灰色系统对于南水河年径流量的拟合精度为84.24%，而且拟合曲线与实际曲线的变化趋势基本一致，可见灰色系统可以较好拟合出南水河年径流量。表2为利用灰色系统的预测模型对2011—2015年南水河年径流量进行预测。根据水文预报的标准(误差低于20%)来看，可见预测的合格率为80%，而且最高年份的误差为22.80%，最低误差为2.71%，因此灰色预测模型对于南水河年径流量的预测结果较为理想。

2.2 基于遗传算法的BP神经网络预测结果

对于南水河的年径流量预测，使用基于遗传算法的BP神经网络是在Matlab软件下进行实验编程仿真的，具体参数设置如下：遗传算法中适应度函数选为模型输出值与实际径流量的误差；个体数目为50；选择方法采用随机遍历采样方法；最大遗传代数设为100代；代沟为0.95；使用单点交叉算子以及离散变异算子，交叉概率以及变异概率的参数分别为0.7和0.001。在BP神经网络中使用3层网络，使用traingdm作为网络的训练函数，隐含层的激活函数选择S型的正切函数，输出层则选择纯线性函数作为激活函数，迭代次数为1000，径流量预测误差取值为0.001，学习速率则设为0.001。

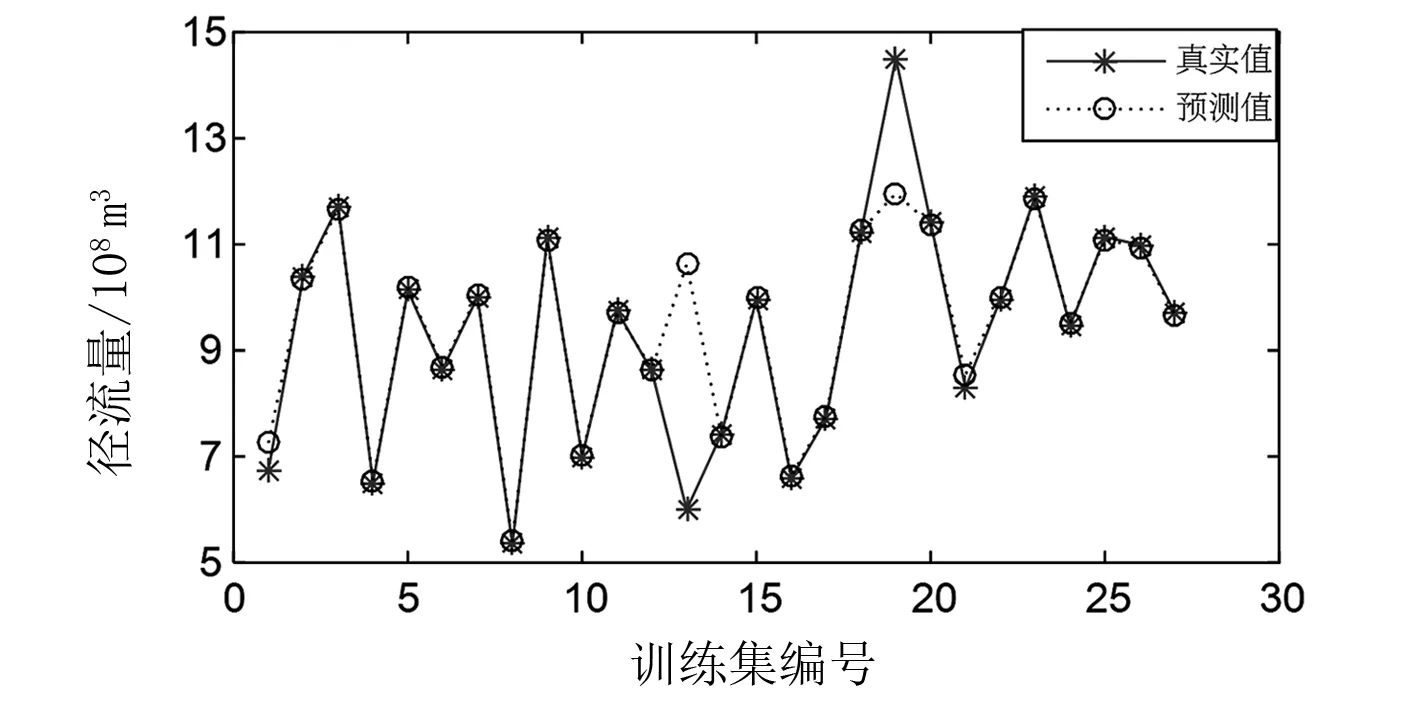
图2 灰色预测径流量拟合值与实际值的比较

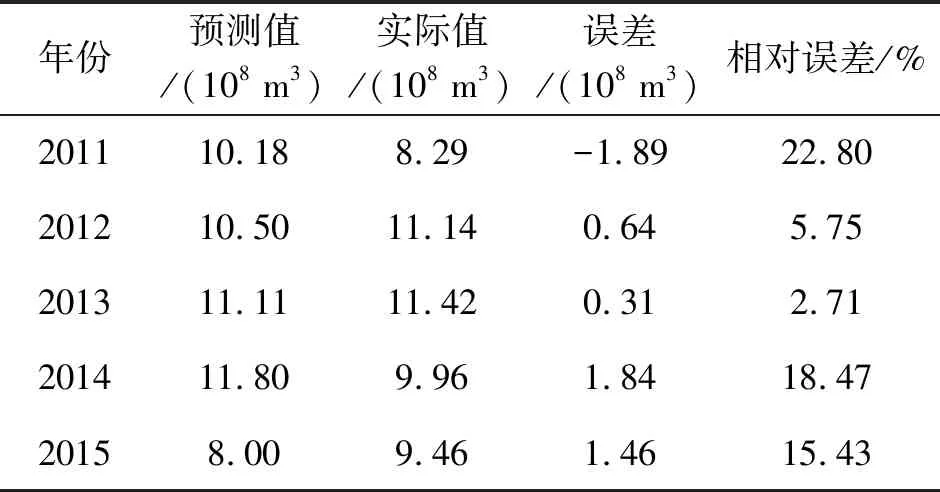
年份预测值/(108 m3)实际值/(108 m3)误差/(108 m3)相对误差/%201110.188.29-1.8922.80201210.5011.140.645.75201311.1111.420.312.71201411.809.961.8418.4720158.009.461.4615.43

经过Matlab对于GA-BP神经网络对南水河年径流量的仿真，如表3所示，可以知道GA-BP神经网络对于南水河往年径流量的拟合误差过大，有部分年份误差甚至超过100%，所以此模型不适用于南水河径流量的拟合。但是从表3可以看出，GA-BP神经网络对于未来年份径流量的预测中，除了2012年的相对误差为38.45%，其他年份以水文预报误差标准来看，都是满足水文预报的标准的，该模型对于这4年的预测都是合格的。

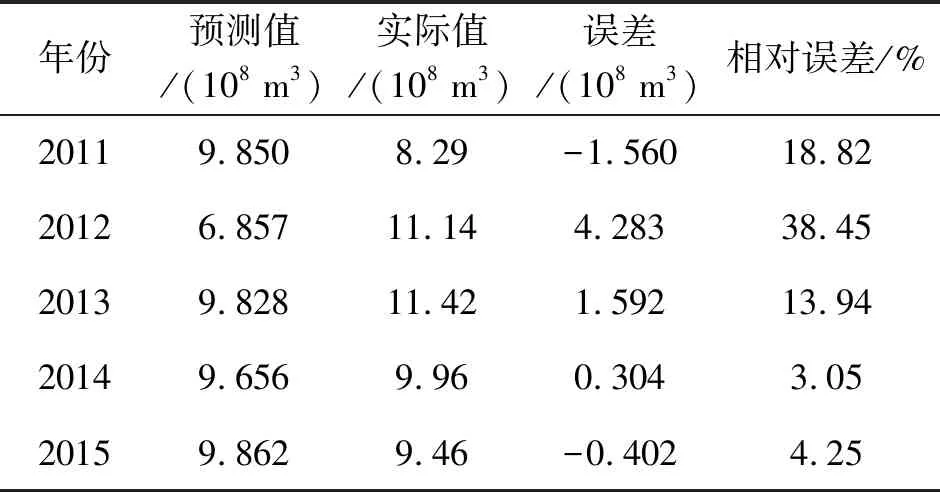
表3 GA-BP神经网络径流量预测结果

2.3 支持向量机预测结果

在对南水河年径流量预测的支持向量机模型中，采用1978—2010年作为模型的训练集，2011—2015年作为模型的测试集。支持向量机的具体参数设定为：核函数类型选择RBF径向基函数；SVM设置类型选为epsilon-SVR回归分析，设置损失函数p为0.01；核函数的gamma参数设为0.022 097，惩罚系数设为1024。在Matlab软件的环境下进行径流量的拟合预测仿真。

图3为支持向量机对南水河1984—2010年径流量的拟合图。可见支持向量机模型对于这27年的拟合结果非常接近，除了少量年份外，其他年份的拟合值与实际值基本重合,支持向量机对于南水河往年年径流量拟合的平均精度为95.67%。根据水文预测的相对误差标准，其中只有1年的拟合值相对误差大于20%，合格率达到96%，故支持向量机模型用于南水河年径流量的拟合效果非常理想。

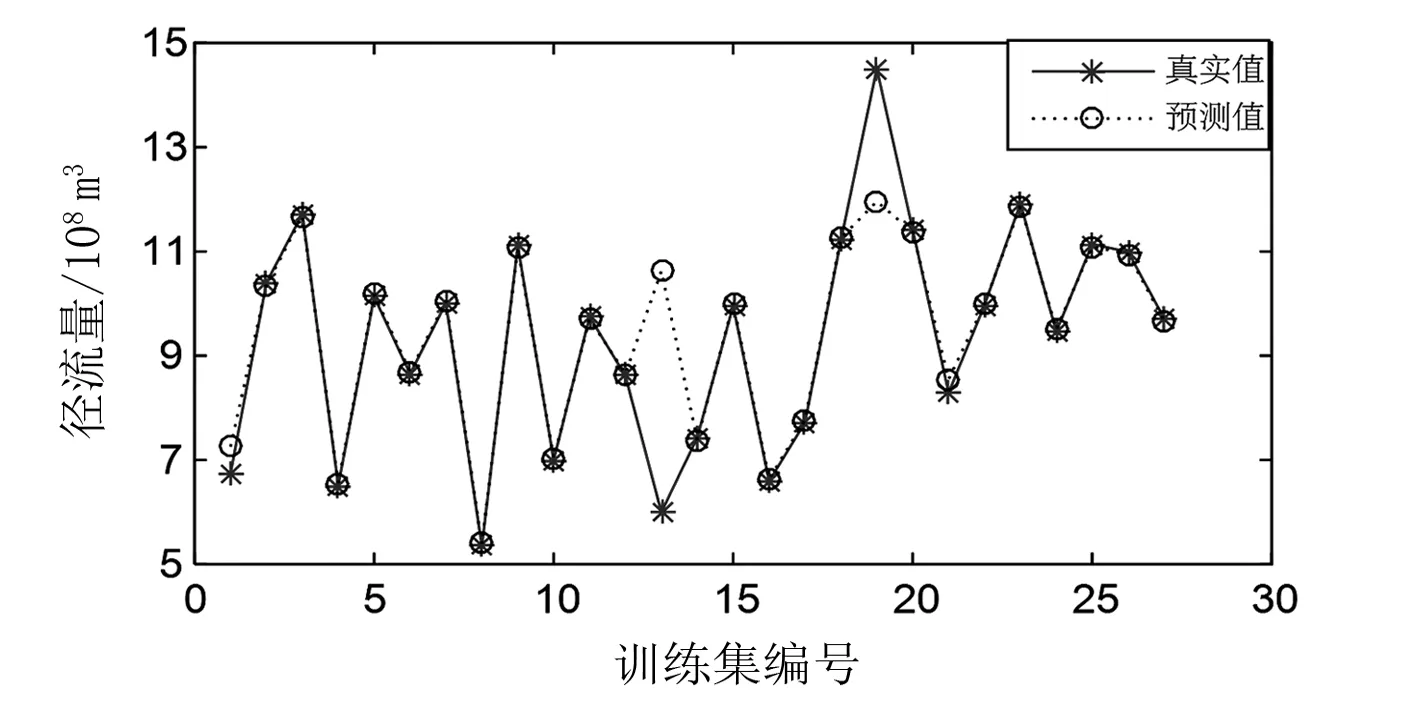
图3 支持向量机径流量输出值与实际值的比较

表4为支持向量机径流量预测，从表中可以看出，支持向量机对2011—2015年南水河径流量的预测值与实际值的变化趋势基本一致，除了2011年误差为3.05%之外，其他4年误差低于1%，因此该支持向量机径流量预测模型用于韶关南水河十分合适，预测效果非常理想。

表4 支持向量机径流量预测结果

2.4 南水河径流量预测

图4为利用上述支持向量机模型对南水河未来年份进行预测，可以看出，2016—2025年南水河年径流量的波动趋势基本与往年一致，其中最大年径流量是2019年的1.197×109m3，最小年径流量预计在2025年，大小为5.29×108m3。

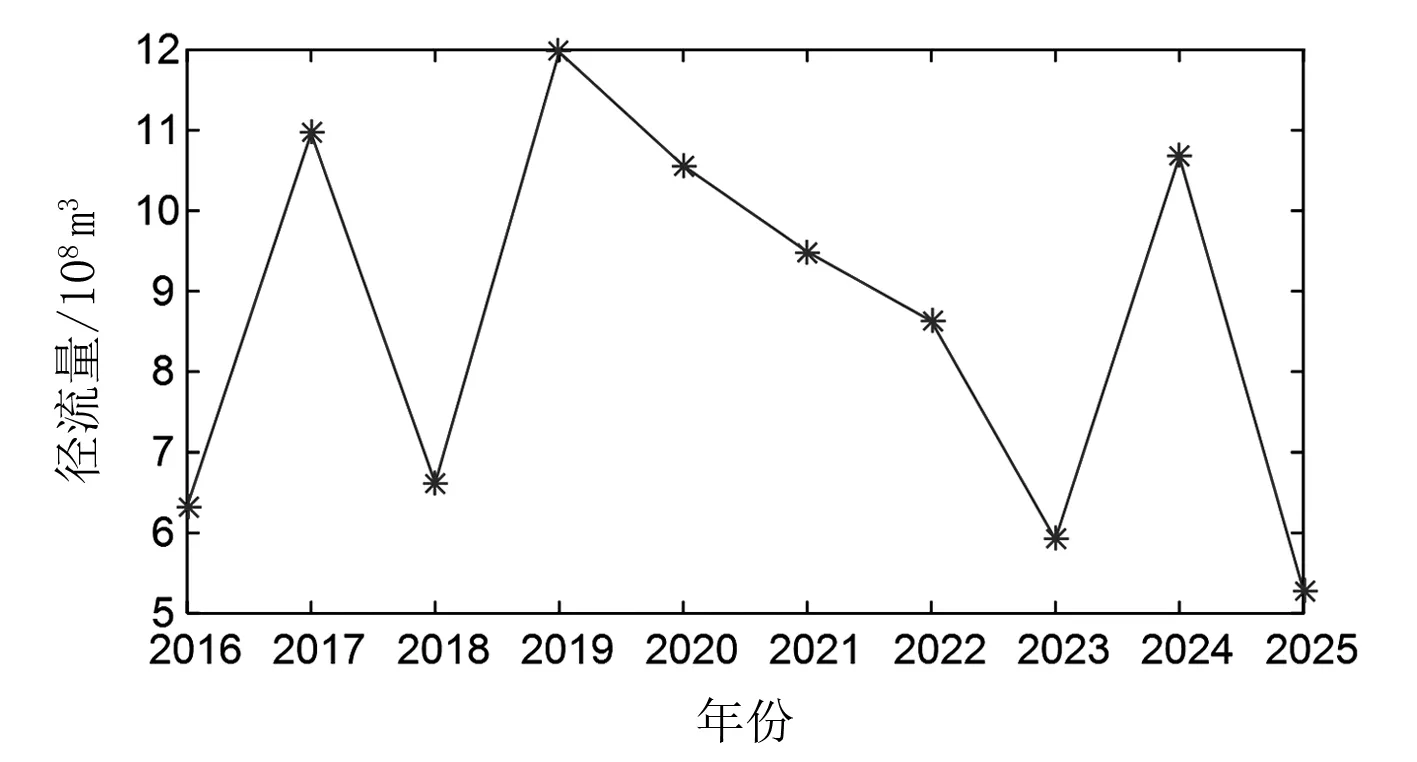
图4 2016—2025年南水河年径流量预测

3 结 语

1)灰色系统理论、基于遗传算法的BP神经网络以及支持向量机3种方法对于南水河年径流量的预测合格率都在80%以上。其中，基于遗传算法的BP神经网络虽然预测合格率高，但是其对南水河往年径流量的拟合度低，所以这种方法不适用于南水河径流量的拟合。灰色系统理论则可以应用于南水河年径流量的拟合及预测中，但其拟合精度以及预测精度不是非常高。而支持向量机无论是对南水河往年年径流量的拟合，还是对年径流量的预测，两者的精度都非常高，所以支持向量机在南水河径流量研究中的效果是十分理想的。

2)通过支持向量机对南水河2016—2025年的年径流量的预测中，可以看出，该河域未来径流量的变化趋势基本与往年一致，说明南水河的水资源比较稳定，对于微电网的建设来说，可以利用南水河水资源补给比较稳定，建设合理数量以及容量的小水电站。