基于有限元法的IGBT模块复合材料等效导热率计算研究
(1.国网四川省电力公司遂宁供电公司,四川 遂宁 629000; 2.国网四川省电力公司电力科学研究院,四川 成都 610041)
0 引 言
在柔性直流输电技术飞速发展的驱使下,作为柔性直流输电换流阀开关器件的IGBT模块日益小型化。在同样的功率情况下,IGBT体积的减小会导致电流密度增大,内部发热增加。如果模块材料散热性能不好,会直接导致内部热量的堆积,温度不断的升高会引起热应力变形严重;如果器件长期在此条件下运行,轻者缩短IGBT的寿命,重者影响其运行可靠性,进而有造成大面积停电的可能:因此,IGBT模块材料的导热性研究俨然已经成为其发展的一个重心,如何改善IGBT模块材料的导热性能成为现阶段的重点工作。
IGBT在柔性直流输电中的应用受到其封装材料及其导热性能的制约。为了得到性能优良的IGBT模块封装复合材料,近年来越来越多的研究者致力于复合材料导热性能的研究[1],结果表明,在基体中加入高导热率的填料可以改善复合材料的导热性能。国内外学者也有很多致力于对材料导热率的理论计算模型进行研究,取得了相应的成果与进展[2-9],但各计算模型也都有一定的局限性,并且适用范围也有限。现有研究中,利用有限元分析方法对IGBT模块复合材料的导热性能进行的研究相对较少[10-14]。
为了提高材料导热性能,下面采用有限元分析方法,在ANSYS软件中建立材料的微观模型并对材料的等效导热率进行仿真计算。同时考虑各种可能的因素,如填料的新装、大小、填料的导热率等对负荷材料导热性能的影响,仿真计算得出各影响因素对复合材料的变化规律,大大节省时间和成本。所提方法对IGBT模块复合材料导热性能研究及IGBT在柔性直流输电中的应用具有十分重要的意义。
1 等效导热率计算方法
1.1 固体热传导
热传导是指发生在物质本身各部分之间或直接接触的物质之间热量传递的现象[15]。由热力学相关定律可以知道,热量是物质运动的一种形式,从微观的角度来看,当粒子的能级轨道发生变化,其能量就会发生相应的改变,由此就会引起物质能量的改变。
由傅里叶公式有:
(1)
式中:q为稳态热通量,W;λ为导热率,W/(m·K);ΔT为热流方向上的温度差,K;Δl在热流方向上的垂直距离,m。
由式(1)可以得到导热率的计算式为
(2)
1.2 等效导热率理论预测模型(Maxwell-Eucken方程)
填充型复合材料的导热性能与基体和填料的导热率有关,同时也与填料颗粒的形状、大小、体积分数、填料颗粒导热率、填料在基体中的分布状态等因素有关[16]。
Maxwell等人[5]提出了基于微粒是孤立存在,彼此之间不存在相互作用的假设的材料导热率计算模型,其模型为
(3)
式中:V为填料颗粒的体积分数;λ为复合材料的导热率;λ1为基体材料的导热率;λ2为填料颗粒的导热率。
在微粒之间相互独立的假设下,得到了Maxwell- Eucken数学模型。从数学表达式可以看出,复合材料的导热率受到填料的体积分数、基体及填料导热率的影响。并且试验表明:当V很小时,复合材料导热率λ的实际值与模型计算值能很好吻合;当V较高时,复合材料导热率λ的实际值与该模型的预测值就相差甚远。因此,Maxwell等人提出的Maxwell-Eucken模型有一定的局限性,只能在填料体积分数较低时才适用。
1.3 基于有限元法的等效导热率预测模型
这里基于有限元分析软件ANSYS对复合材料等效导热率的计算方法进行研究,建立模型并与理论预测模型以及文献[17]进行对比分析。对比结果见表1:Vol.%为体积百分数;D为颗粒的平均直径;λ1为基体的导热率;λ2为填料的导热率;λ为文献[17]计算的等效导热率;λ′为理论模型计算出来的等效导热率;λ″为所提有限元方法计算出来的等效导热率。由表1可以看出,所提方法的计算结果与Maxwell-Eucken模型理论值以及文献[17]的试验结果吻合度很高。由此可见,所采用ANSYS的仿真计算方法是可行的。
2 基于有限元法的等效导热率预测方法
2.1 有限元ANSYS介绍
在没有内热源、稳态条件下,温度t的分布遵循导热方程[18]为
(4)
要求解此方程,有3类边界条件,分别为:

表1 导热率结果对比 单位:W/(m·K)
1)规定边界上的温度值t为一个恒定常数。
t=const
(5)
2) 规定边界上的热流密度值为一个恒定常数。
(6)
式中:n为表面的法向量;λ为材料的导热系数。
3)规定周围流体的温度、材料与流体间导热系数。
下面的仿真过程中,仅仅只涉及前两种边界条件。
2.2 建模与边界条件设置
在有限元分析软件ANSYS中建立复合材料模型:基体是边长为300 nm的正方体;填料颗粒平均分布27个颗粒,颗粒形状为球体、正方体。
边界条件:微观模型相对两面的壁面温度分别为100 ℃和0 ℃,另外4个面绝缘。
仿真考虑了:填料颗粒的形状为球体、正方体;填料颗粒的体积分数为5%、10%、15%、20%、30%、40%;填料颗粒的导热率为10 W/(m·K)、20 W/(m·K)、 30 W/(m·K);填料颗粒的团聚等因素对复合材料等效导热率的影响。
经过建立模型、设置材料参数、划分网格并求解。求解后,根据模型温度场的分布,按公式对复合材料等效导热率进行计算。
2.3 有限元法对复合材料等效导热率预测
图1为用ANSYS建立的模型,其中填料颗粒均匀分布在基体材料内部。边界条件为微观模型左、右壁面温度分别为100 ℃和0 ℃,另外4个面绝缘。
图2至图4均为球形颗粒均匀分布,在体积分数为10%情况下的结果。图2是温度场分布图,其中:图2(a)是基体材料的温度分布;图2(b)是填料颗粒的温度分布;图2(c)是中间9个填料颗粒的温度分布。由图2可以得出,温度沿着x轴依次减小,热流量方向是由x负向指向x正向。
图3和图4分别是热梯度分布和热通量分布图。填料颗粒附近的热梯度和热通量比基体材料的热梯度和热通量大,因为填料颗粒的导热率大于基体的导热率。
根据模型温度场的分布,对复合材料等效导热率进行分析计算。
=0.263 5 W/(m·K)
(7)

图1 均匀分布模型
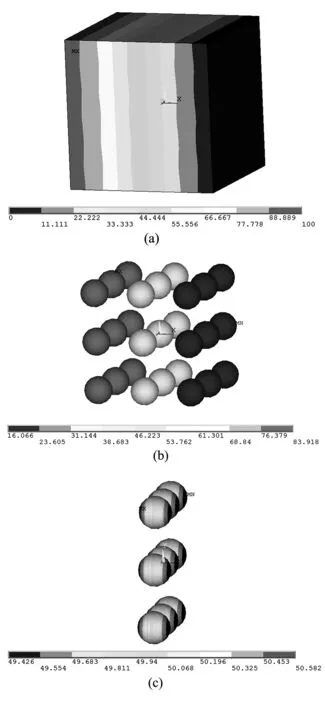
图2 温度场分布

图3 热梯度分布

图4 热通量分布
用Maxwell-Eucken理论模型计算体积分数为10%,球形颗粒均匀分布时,复合材料等效导热率为0.223 6 W/(m·K)。用有限元方法得到复合材料等效导热率为0.249 8 W/(m·K),与Maxwell-Eucken理论值的误差为11.72%,进一步说明有限元方法预测复合材料等效导热率是可行的。
3 复合材料等效导热率的影响因素
复合材料的导热性能最终取决于填料及其在基体的分布情况[16]。当填料含量较低时,其对材料导热性能的贡献并不大;当填料含量较多时,复合材料的力学性能受到影响,其含量增至某一值时,填料微粒之间相互作用并形成一定的链状和网状。当热流的方向与链条的方向一致时,材料的热阻最小,宏观反应就是导热率高,导热性能好;反之则导热性能差。
填充型复合材料导热性能的影响因素[16]有:聚合物基体的种类、特性;填料的导热率、形状、大小、体积分数、分布情况等。
3.1 填料颗粒导热率的影响
为了得到更好导热性能的复合材料,可以向基体材料中添加高导热率的填料颗粒来提高复合材料的等效导热率[7]。采用所提方法计算的结果见表2和表3,表中的填料1、填料2、填料3的导热率分别为10 W/(m·K)、20 W/(m·K)、30 W/(m·K)。图5中4幅图分别是体积分数为10%、20%、30%和40%时,复合材料等效导热率与填料颗粒导热率的关系。从图5中可以看出随着填料颗粒的导热率增加,复合材料的导热率也增加。

体积分数/%复合材料导热率/(W·m-1·K-1)填料1填料2填料350.231 20.232 00.232 0100.263 50.265 30.265 3150.357 60.361 80.3618200.35610.36110.3611300.47130.48160.4816400.749 20.776 30.7763

表3 正方体颗粒对复合材料导热率的影响
3.2 填料颗粒体积分数的影响
在基体材料中添加高导热率的填料颗粒,这种方法提高了复合材料的等效导热率。但随着填料的增加对复合材料的热性能到底有什么影响,还需要用仿真来进行验证。
图6中的3条曲线代表填料颗粒的导热率λ2分别为10 W/(m·K)、20 W/(m·K)和30 W/(m·K)时不同体积分数下的导热率变化情况。从图6可以看出,无论是球状颗粒还是正方体颗粒,复合材料的导热率随着填料颗粒体积分数的增加而增加,但非线性的关系。

图6 复合材料等效导热率与填料体积分数的关系
3.3 填料颗粒形状的影响
研究表明,填料颗粒的形状对复合材料的导热率有一定的影响[17,19-21]。由图7可以看出填料体积分数在15%~20%区间,方形填料和球形填料的复合材料导热率有一个交叉点A:
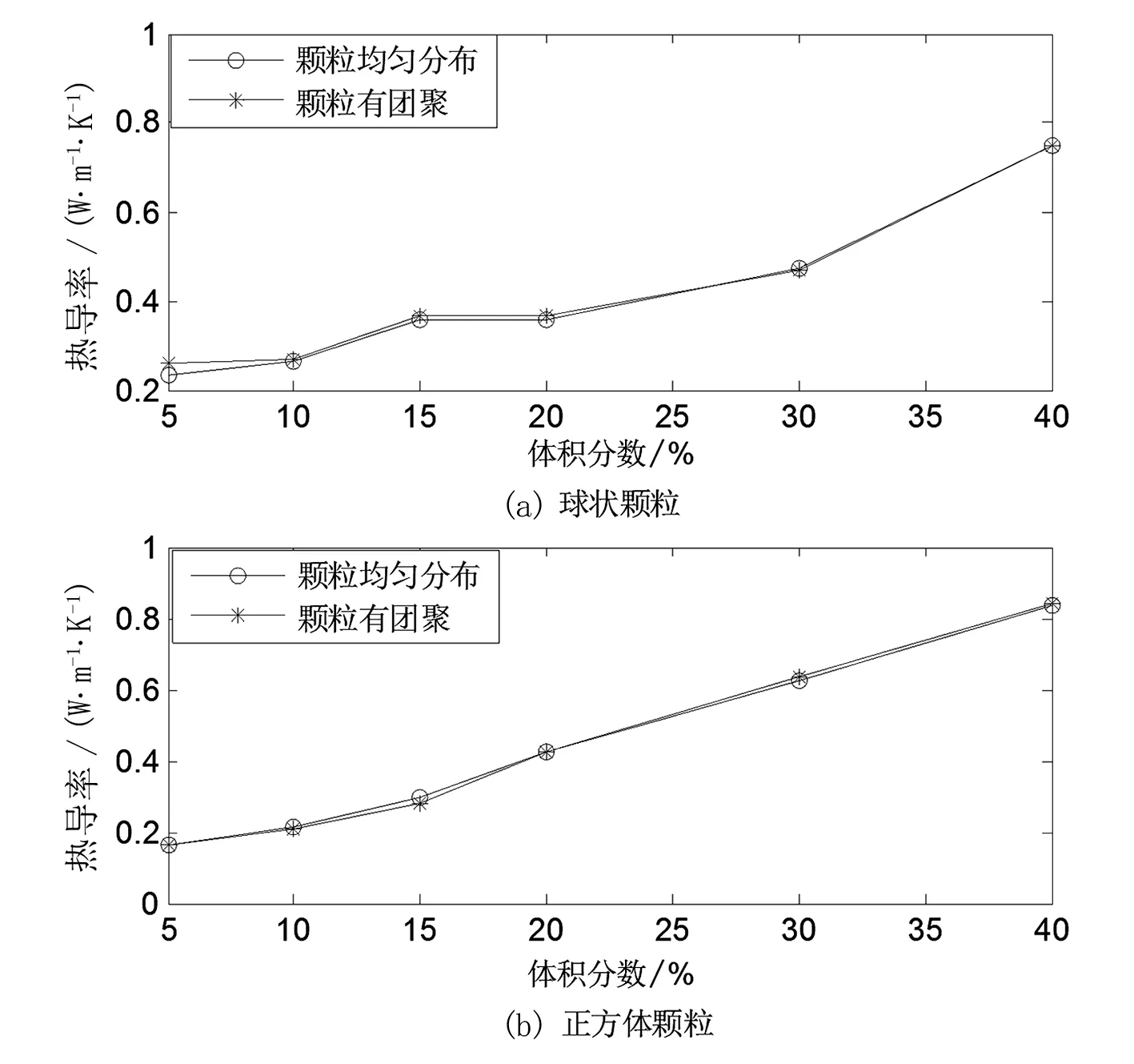
当体积分数V 当体积分数V>A时,方形填料复合材料的等效导热率大于球形填料。 图7 复合材料等效导热率与填料颗粒形状的关系 实际情况中,复合材料的填料不论是方形还是球形,都不可能均匀分布在基体材料中,为此建立了填料有粒子团聚的模型与填料粒子均匀分布模型(见图8),在填料颗粒导热率为10 W/(m·K)时,分别计算复合材料的等效导热率并进行对比,得到的结果见表4和图9。 从表4和图9的计算结果表明,有粒子团聚的填料与均匀分布的填料相比,复合材料的等效导热率差别微乎其微,甚至可以说几乎没有影响,由此就说明粒子团聚现象几乎对复合材料等效导热率没有影响。同时,这个结论与文献[20]中得到的试验结论相吻合。 图8 ANSYS颗粒团聚模型 表42=10W/(m·K)时,不同颗粒形状对等效导热率的影响 体积分数/%球状颗粒/(W·m-1·K-1)正方体颗粒/(W·m-1·K-1)均匀团聚均匀团聚50.231 20.260 80.165 00.162 9100.263 50.267 30.213 4 0.209 0150.357 60.367 90.297 30.280 4200.356 10.367 20.424 20.423 7300.471 30.470 7 0.625 30.635 8400.749 20.749 1 0.838 30.839 8 图9 复合材料中填料均匀分布与有粒子团聚对比 基于现有文献研究的基础上对IGBT封装复合材料的导热率进行的研究,利用先进的有限元数值分析方法,同时考虑实际情况,分别分析了填料的大小、形状、体积分数等因素对复合材料导热率的影响规律,进而对复合材料的导热性能进行有效的预测,得到以下结论: 1)对比Maxwell-Eucken模型、参考文献中的试验数据以及所提有限元法对有效导热率的计算结果,三者结果一致,说明有限元法仿真计算的可行性。 2)填料的形状、大小、体积分数、填料颗粒导热率等对复合材料导热率的影响:随着体积分数的增加,复合材料导热率增加;复合材料在填料体积分数很低时,添加球状颗粒的复合材料等效导热率大于添加正方体颗粒的复合材料;在体积分数较高时,添加正方体颗粒的复合材料等效导热率大于添加球状颗粒的复合材料;随着填料颗粒的导热率增加,复合材料的导热率增加。 3)粒子团聚现象几乎对复合材料等效导热率没有影响。
3.4 粒子群的影响


4 结 语

