基于MLP法的磁浮列车非线性系统的稳定性分析

杨志安，崔佳磊

(1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；.华北理工大学 机械工程学院，河北 唐山 063210)

0 引言

磁浮列车通过电磁力将列车控制在一定高度，实现列车与轨道之间无机械接触，然后通过直线电机驱动列车。它具有速度快、爬坡能力强、能耗低、运行噪音低、安全、舒适、污染小等优点[1]。磁浮列车的悬浮能力直接决定了车辆的承载能力，而悬浮能力的大小取决于悬浮控制系统。悬浮控制的基本要求是保证列车在各种内外干扰力作用下能够稳定的运行。

研究磁浮列车稳定性问题，首先要建立正确的动力学模型，磁浮列车属于机电磁耦合系统，拉格朗日-麦克斯韦方程是建立机电系统模型的一种核心方法。经典的拉格朗日-麦克斯韦方程是基于线性的电场能We和线性的磁场能Wm，以电荷、电流作为广义坐标得到的[2]。2007年文献[3]中推广了拉格朗日-麦克斯韦方程的应用范围，使之适合于电磁非线性情况。2012年，文献[4]将机电系统的状态变量与力学系统的广义坐标相联系，得到了经典形式的拉格朗日-麦克斯韦方程，使机电分析动力学的核心内容更加完善。

MLP法，是在摄动法小参数的基础上引入非小参数，小参数的来源是将非线性有关的参数利用幂级数进行展开，并且展开的要求是其后的每一项都要小于前一项。非小参数是由小参数变换而来。将非线性微分方程转化为线性随机微分方程组，最后用此方法就可以求解了。与等效线性化方法一样，MLP法只能得到响应的时域信息，而不能得到响应的频域信息，因为非线性系统的频率没有可保存性，所以频域信息是不稳定的， 理论上难以获得[5]。

Wu等人提出了一种基于T-S模糊数学模型的非线性电磁悬浮系统模糊控制方法，仿真结果表明，该方法在处理有界扰动时有效，但同时却增加了控制器设计的复杂度[6]。施晓红等人从磁浮列车-轨道耦合的非线性特性的角度研究了静悬架条件下磁浮列车-轨道耦合系统的控制参数、轨道参数与振动特性之间的相关关系[7]。杨霞等人研究了单磁悬浮系统，建立了磁悬浮系统在平衡点的状态方程，并采用极点配置法使系统满足稳定性条件，在此基础上，对磁悬浮系统进行了数值模拟分析，最后得出结论，状态空间控制方法能有效地稳定磁悬浮系统[8]。

在众多的磁浮系统研究中，学者们对转向架、电磁力、车-轨耦合振动、车辆运行稳定性以及悬架控制器的设计等问题进行了研究，主要研究方向集中在磁浮列车的线性系统上。本文主要根据拉格朗日-麦克斯韦方程建立关于磁浮系统的非线性动力学模型，利用MLP法来研究主共振的幅频响应方程。

1 磁浮列车悬浮系统动力学模型的建立

常导型磁浮列车悬浮系统简图如图1所示，列车的车厢下方装有电磁铁，电磁铁吸向“T”型钢轨，当电磁铁绕组中的电流及在电磁铁与钢轨间的气隙均为标称值的情况下，悬浮拉力和车厢的重力平衡。

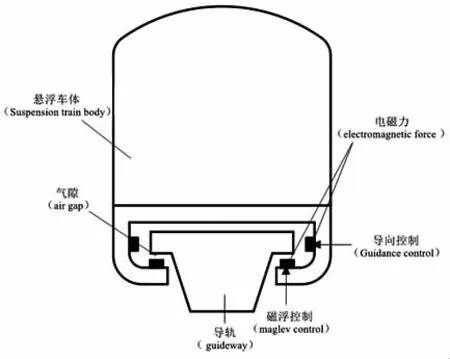
图1 磁浮列车悬浮系统简图

当磁浮列车车厢沿铅垂轴方向做直线平动，且在通电之后处于平衡状态时，电磁铁与钢轨间的气隙为标称值，车厢质心与原点O重合。以Δy表示车厢的小位移，以i表示电磁铁绕组中的电流。所研究的磁悬浮机电系统的广义坐标为Δy，i。磁浮系统的物理模型见图2。

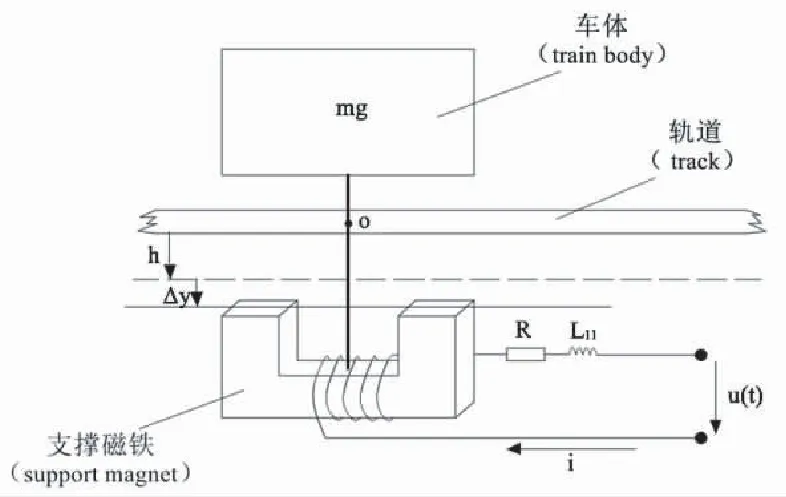
图2 磁浮系统的物理模型

将悬浮车厢看作一个刚体，利用刚体平动的动能公式得到车厢的动能公式：

(1)

悬浮车厢的重力势能为：

V=mgΔy。

(2)

磁场能量计算公式为：

(3)

式中V为磁场包围的体积，B为磁感应强度。

假定电磁铁与钢轨间的气隙h-Δy和U型电磁铁的截面积s相比很小。这时在电磁铁与钢轨之间的气隙中磁场可以认为是均匀的，并且可以忽略边界效应，在钢轨、磁铁、气隙之间以外的漏磁场可以忽略。假定在钢轨与磁铁中的磁导率μ非常之大，因此沿磁铁与钢轨的体积内的磁能相比于磁铁与钢轨间隙内的磁能很小，因此可以忽略。根据以上的假设对式(3)进行计算时，在两个气隙内的磁感应强度B可以看作常量，于是由式(3)计算得到：

(4)

式中μ0为气隙磁导系数。

通过电磁铁的磁通为：

φ=BSN，

(5)

上式中N为绕组的匝数。

根据磁通和电流成正比的关系可得：

φ=L11i，

(6)

上式中，L11为线圈的自感系数，i0为标称电流。

由式(5)及式(6)可得到磁感应强度为：

(7)

将式(7)代入磁能公式(4)中，得到

(8)

同时磁能公式还可以表示为：

(9)

同样由式(8)及式(9)可以得到自感系数关于广义坐标的表达式：

(10)

再将式(10)代入式(9)得到磁能关于广义坐标以及电流的表达式：

(11)

根据能量守恒定律，利用拉格朗日-麦克斯韦方程来建立磁浮系统的动力学模型，将式(1)(2)(11)代入Lagrange方程：

L=T+Wm-V=

(12)

耗散函数的表达式为：

(13)

上式中，b为车厢运动的粘性阻力系数，R为线圈的电阻。

假定不存在机械的非保守广义力，用u(t)表示作用于电磁铁中的电压。为了保证列车车厢的稳定性，这个电压要依赖测量电磁铁与钢轨间气隙大小的指示传感器，当气隙增大时则电路中的电流也必须增大，以便增加磁铁与钢轨间的电磁拉力，使车厢回到平衡状态；相反，当气隙减小时则需要减小电流的输入，以便减小电磁拉力，使车厢保持平衡状态。

磁浮列车悬浮系统的拉格朗日-麦克斯韦方程的形式为[2]：

(14)

将式(12)及式(13)代入式(14)中，并经过一定的微分运算得到磁浮列车车厢的运动微分方程：

(15)

式(15)中，(b)式的第一项是非线性项，为钢轨间气隙的倒数与电流的变化率的乘积，(b)式的第二项同样是非线性项，(a)式的第三项也是非线性项，所以该方程组是一个三阶的非线性方程。因为其计算复杂，且不好处理，所以现阶段几乎没有学者对其非线性项进行详细的研究。

2 主共振分析

假设式(15)中u(t)=u0cosωt，也就是说将电压看作是激励电压，u0是常数，当车厢处于平衡位置时

(16)

将式(16)代入式(15)可以得到u0和i0的值：

u0=Ri0；i02=2mg/L0，

(17)

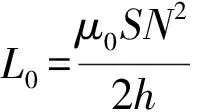
当车厢位移很小时，即Δy≪h时，磁铁中的电流和本生的标称值i0相近，此时引入小参数α，此时式(15)中的电流i为：

i=i0+αx。

(18)

利用上述理论将式(15)化为：

(19)

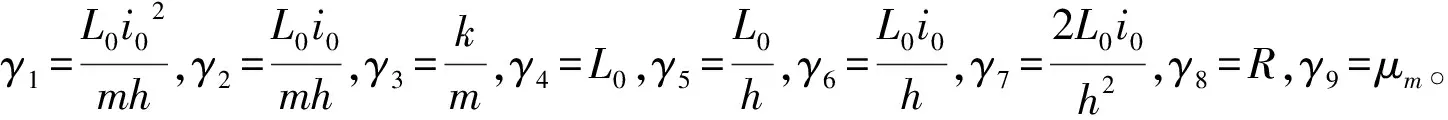
将式(19)中的第2式子代入第1式得到：

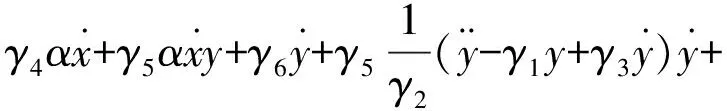
(20)

继续完善式(19)，得：

(21)

(22)

令ω2=ω02+εω1+ε2ω2+…。

(23)

引入参数变换，此时小参数α用非小参数ε近似表示：

(24)

反解出非小参数ε：

(25)

将式(25)代入式(23)可得：

(26)

(27)

对y采用摄动法[9]展开：

y=y0+αy1+α2y2+…。

(28)

利用上述论述，将式(22)化为：

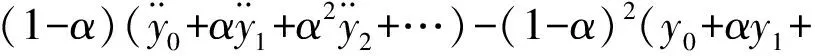
(29)

比较方程两边α的幂次得：

(30)

(31)

(32)

式(30)的基解，即式(22)的零次近似解：

y0=Ae-τ+Beτ。

(33)

将基解式(33)代入式(31)，得到动力学模型的一次可求永年项的表达式。同理，利用式(32)可得到方程(22)的二次可求永年项表达式。再根据永年项的定义，即随时间增加趋于无穷的项[10]，也就是在所得到的二次可求永年项表达式中含有eτ，e2τ，e3τ，也就是说系统发生振幅无限的共振。若要使磁浮系统做周期平稳运动，需要消除永年项。为此令所得式中的eτ，e2τ，e3τ项的系数为零。

(34)

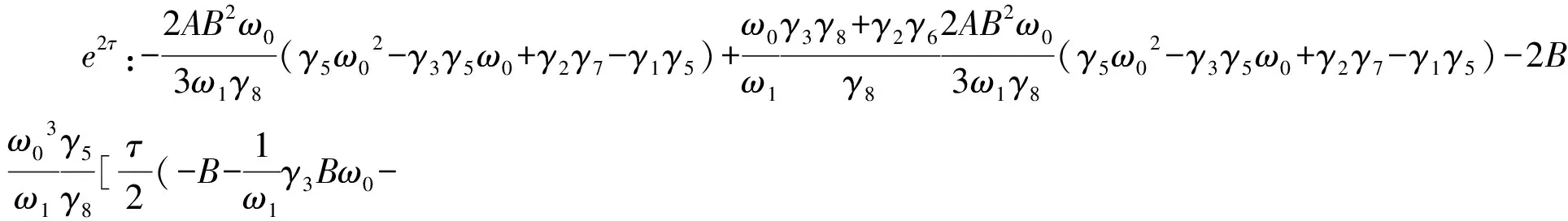
(35)

(36)

3 数值模拟

(37)

在利用Matlab进行计算之前，需要为式(37)中的各个参数赋值，且确定式(37)的初始条件。

各参数的取值分别为：R=1 Ω，m=61 000 kg，μ0=4π×10-7H/m，S=0.021 m2，i0=30 A，N=356，k=8.46×104N·s/m，h=0.01 m，ω=100 π rad/s，u=220 V。

设式(37)非线性微分方程组的初始条件分别为：

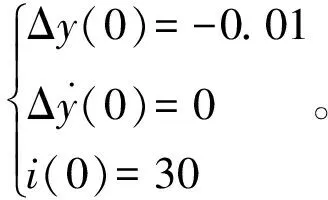
(38)

通过四阶龙格库塔法计算并绘制出50 s内磁浮列车悬浮系统在空载、满载、过载不同载荷下的时间响应曲线以及相图，见图3-8。

图3 m=60 000 kg时间响应曲线

图4 m=69 000 kg时间响应曲线

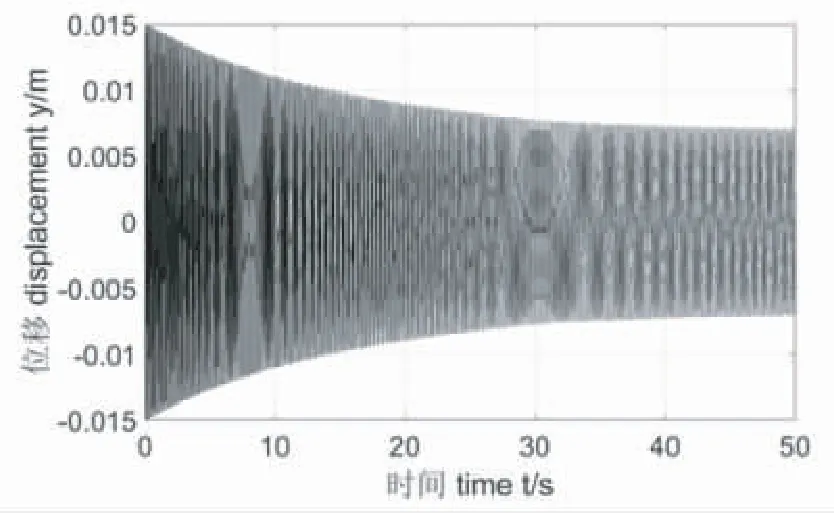
图5 m=70 800 kg时间响应曲线

图6 m=60 000 kg相图

图7 m=69 000 kg相图

图8 m=70 800 kg相图

从图3到图5可以看出，随着磁浮列车质量的增加，列车初始位移会增大，但随着时间的推移，列车都会趋于稳定。从图6到图8的相图可以看出，随着磁浮列车质量的增加，列车初始位移会增大，列车的垂向振动速度在减小，这表示列车会趋于稳定。

4 结论

(1)选取间隙和电流为广义坐标，利用拉格朗日-麦克斯韦方程建立磁浮列车悬浮系统的运动模型。该模型属于三阶非线性微分方程。

(2)改变MLP法的基解形式，是考虑到微分方程的形式同传统的振动微分方程不同，其基解的表达式为指数形式，不同于正刚度的三角函数形式，最终得到三个不同指数幂的表达式，这也不同于正刚度的三角函数形式，三角函数形式只能有两个表达式，指数形式涉及到的不定参数过多而无法进行求解。

(3)在空载、满载、过载情况下，模拟时间为50 s时的悬浮系统振动时间响应曲线，由相图可知，列车质量增加，列车初始位移会增大，但列车起动后经过一定的时间，系统振动趋于稳定。