一种基于局部球面约束的GPS单频瞬时定向方法*

陈万通 尚正辉 刘 庆

1.中国民航大学天津市智能信号与图像处理重点实验室, 天津300300 2.上海航天电子技术研究所, 上海201109

寻北与定向系统一般广泛应用于武器控制系统、飞机、船舶及行走机械等机动载体上，要求测向系统具有精度高、实时性好、免维护和易安装等特点。相比于传统的惯性器利用GPS信号进行航向解算具有成本低、无累积误差和安装方便等优势，已经成为当前载体测向的主要手段之一[1]。GPS测向不同于常规的单点定位技术，该技术基于载波干涉原理，通过差分手段削减电离层和对流层误差、轨道误差、卫星和接收机时钟误差，进而实现高精度的相对定位，基线测量精度可达亚厘米级。由于载波是一种周期性的正弦信号，进行相位测量时存在着观测信号的整周模糊度问题，只有正确求得整周模糊度，高精度的相对定位和角度测量才可以实现。相比于多历元解算和多星座解算，GPS单频瞬时测向技术在避免整周跳变的同时兼具低成本优势，成为当前该领域的研究热点[2]。利用基于基线长度约束的LAMBDA算法(C-LAMBDA)是GPS瞬时测向的一种有效算法，但该算法在单频应用时系统的成功率显著依赖于可见星数目和伪距的精度，因此，既不适用于城市峡谷等遮挡环境中的应用，也不适用于伪距精度较低的低成本接收机[3]。本文对原算法的性能进行了理论分析，提出了一种带有局部球面约束的整数最小二乘估计方法，改进算法不再依赖于高精度的伪码测距辅助求解，并充分将概略测向信息融入到短基线观测模型中，增强了模型强度，提高了定向解的可靠性，并为多传感器联合测向提供了一种解决策略。改进算法的成功率对可见星数目的变化敏感度较低，对于拓宽GPS测向技术的实际应用场景具有重要意义。

1 GPS瞬时测向理论模型

GPS定向技术通过精确解算由2个天线构成的短基线在当地地理水平坐标系下的三维矢量实现高精度的航向估计，若载体航向角为ψ，俯仰角为θ，基线长度为l，则基线矢量在东北天地理坐标系下可表达为：

(1)

对于GPS瞬时测向系统，假定当前历元的卫星可见数m大于4颗并且实现接收机到卫星LOS矢量的计算，基于载波干涉原理和应用双差方法，则其双差载波/码联合观测方程分别为[4]：

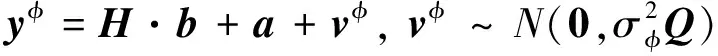
(2)

(3)

其中，y表示双差载波和双差码的联合观测矢量，维度为2m-2；A和B分别为a和b的系数矩阵；v为y的观测噪声矢量；Qy为其方差协方差矩阵。该模型基于最小二乘准则，等价于求解：

(4)

(5)

对应的方差协方差矩阵为

(6)

基于带有二次型约束的整数最小二乘搜索理论[6]，式(4)中，整周模糊度的参数估计为：

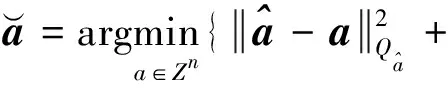
(7)

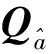
(8)

注意到，若σρ/σφ取值较大以及m取值较小都会引起整周模糊度浮点解的精度降低。由此，C-LAMBDA算法在低成本接收机上应用时，因较差的伪距观测精度最终导致测向成功率较低；在城市峡谷等环境中应用时，因遮挡造成的卫星可见性不佳，也会导致成功率较低。研究表明，在整周模糊度估计过程中采用多约束条件是提高成功率的重要手段之一[8]。

2 基于局部球面约束的改进模型

2.1 局部球面约束

在GPS瞬时测向理论模型中，基线所确定的解空间为一球面，球半径为l，球心位于主天线的相位中心。在实际应用中，载体姿态的相关先验信息，例如来自磁罗盘和加速度计的概略航向测量[9]、来自倾角计的俯仰测量[10]以及速度航向测量，可将解空间限制为局部球面区域，基于这一约束条件，理论模型可以修正为：

(9)

目标函数等价为

(10)

其中,Ω代表局部球面区域，包含由航向角真值ψ和俯仰角θ确定的姿态点(ψ,θ)。

2.2 改进模型

在局部球面区域内进行搜索，假定候选的姿态点为(ψs，θs)，则对应的候选基线解为：

(11)

候选基线解与真实基线解之间的误差为δb，即

bs=b+δb

(12)

将式(12)代入式(2)的双差载波观测方程中，可得

yφ-H·bs=a+H·δb+vφ

(13)

(14)

(15)

根据式(14)求得as的浮点解及其方差协方差矩阵分别为：

(16)

根据式(15)求得a的浮点解及其方差协方差矩阵分别为：

(17)

在改进模型中，目标函数等价为

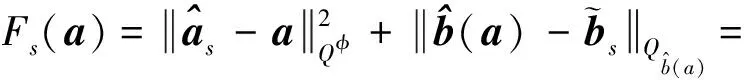
(18)

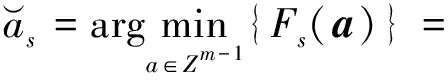
(19)

最佳候选姿态解为

(20)

在上述改进模型中，不涉及码观测量，因此不要求接收机输出高精度的伪距测量，同时对于瞬时解算也无秩亏问题。此时

(21)

对比式(8)，整周模糊度浮点解的精度显著提升，决定了理论上改进算法的成功率高于C-LAMBDA算法。

2.3 性能分析

在改进模型中，需要在局部球面区域内建立栅格，即从离散的候选姿态点集合中逐一计算目标函数值，假定离真实姿态点(ψ,θ)球面距离最近的候选点为(ψc,θc)，则该候选点处基线误差为

(22)

假定在球面区域内航向和俯仰的搜索步长分别为ηψ和ηθ，则候选点为(ψc,θc)与真值的偏差为

(23)

若搜索步长足够小，可近似认为

(24)

由式(23)和(24)可知,|δbc|满足如下关系：

(25)

即候选点为(ψc,θc)与真值的偏差与基线长度、基线指向和搜索步长有关。为了提高改进模型的成功率，实际应用中应该采用较短的基线和更为精细的搜索步长，但考虑到基线越短测向精度越差，搜索步长越小算法耗时越多，因此建议在成功率、精度和算法耗时之间进行折中。

2.4 搜索策略

为了提升搜索效率，需要确定一个包含真实姿态点且尽可能小的局部球面区域内建立栅格，假定候选姿态点的索引为i，姿态点记作(ψi，θi)，则对应的基线解为

(26)

1)首先，令i=0，设定初始搜索空间的大小为

(27)

该空间至少包含一个候选值a0,ILS。

经过迭代数次上述搜索步骤，搜索空间迅速缩小，并且多数情况下步骤2)无解，即无需进入计算量较大的步骤3)，因此上述步骤可以极大提高搜索效率。

3 系统设计

为了进一步验证新算法在实际环境应用中的性能，设计了基于倾角传感器和磁罗盘辅助的GPS单频瞬时定向系统。系统的核心硬件部分包括2个GPS单频测量型天线，2台GPS接收机，1个倾角传感器(SCA-100T-D02)，1个地磁传感器模块(RM3100)以及S5PV210处理器，所有核心部件集成在PCB底板上，如图1所示。通过改变底板的长度设计可调节双天线几何中心的间距，实现不同基线长度的测向系统。

图1 GPS单频瞬时定向系统

为了降低系统的成本，GPS接收机采用基于UBLOX LEA-6T导航芯片，该芯片支持原始载波相位数据的输出，支持星历数据的输出，超低功耗，体积小，便于和四馈点的测量型天线集成在一起，板卡中天线单元设计如图2和3所示。

图2 四馈天线单元(正面)

图3 四馈天线单元(背面)

在图1所示GPS单频瞬时定向系统中，位于板卡中部的S5PV210处理器主频可达1GHz，能够将2路GPS原始数据通过UART口进行实时采集，并依据倾角传感器和地磁传感器提供的概略姿态信息确定包含真实姿态点的局部球面区域，最终通过RS232串口将精确估计的航向信息输出给航向显示设备和存储装置。

4 实际测试

4.1 静态实验

为了评估系统在不同基线长度状态下的成功率，分别进行了多组静态实验，实验场地为城市街道十字路口，每组实验可见卫星观测数目仅为5～6颗，观测历元均为1000个，历元间隔1s。为了使算法中涉及的局部球面区域必定包含真值在内，此次实验中，实际依据地磁传感器测量值正负25°划定航向角栅格以及依据倾角传感器测量值正负5°划定俯仰角栅格，搜索步长η分别选定0.2°,0.3°和0.5°三种情况评估定向成功率与平均计算用时。表1给出水平放置的不同基线长度下定向成功率与平均计算用时。

表1 不同基线长度下定向成功率与平均计算用时

可以看到，定向成功率随着基线长度的缩短呈上升趋势；搜索步长越精细，成功率越高，但由于候选姿态的数量增多，牵涉计算所花费的时间也越多，这与2.3小节的理论分析相一致。

4.2 动态实验

为了进一步测试算法在动态情况下的性能，利用0.45m基线的定向系统进行跑车动态测试，测试地点为城市环境下一东西走向的狭长绿化带，跑车的运动重复周期为5周。图4给出了跑车试验的轨迹图，图5给出了期间可见星数目的变化情况。图6为动态试验的测向结果，其周期性变化规律与跑车运动轨迹基本一致，成功率接近100%，证明了算法在城市环境下的有效性。

图4 GPS单频动态跑车试验的轨迹图

图5 GPS单频动态跑车试验的可见星数目

图6 动态试验结果

5 结论

针对GPS单频瞬时定向在城市环境和低成本接收机上应用受限问题，提出一种带有局部球面约束的整数最小二乘估计方法，该算法优点在于：仅利用载波相位观测值实现瞬时定向，不需要接收机提供高精度的伪码测距，无秩亏问题；将姿态概略信息视作球面区域约束，并充分融入到整周模糊度的估计环节，增强了整周模糊度估计的成功率，提高了定向解的可靠性。实际试验表明，本方法可以适用于城市峡谷等卫星可见性受限环境下的定向解算。