基于决策更新的多级火箭弹道重规划技术研究
马昊磊 李学锋
1. 北京航天自动控制研究所,北京 100854 2. 宇航智能控制技术国家级重点实验室,北京 100854
在实际飞行任务中,运载火箭可能由于故障原因偏离原先设计好的标称弹道,继续沿用标称弹道条件下的制导控制方案将难以完成任务。增强飞行安全与可靠性是未来火箭的发展目标,这就要求火箭既能将载荷高精度送入预定轨道,还能在发生故障偏差时重新规划飞行弹道。
弹道重规划包括任务决策和轨迹规划2部分内容。当飞行过程中出现异常状态时,需要通过任务决策确定下一步的行动目标。任务决策设计需要综合利用全箭信息,根据飞行状态判断是否开展重规划工作[1],采用轨道设计反方法[2]与组合性能指标函数[3]等设计思想,分析飞行器的机动变轨能力,进而确定满足要求的最优任务轨道。轨迹规划则是将目标轨道根数作为终端约束,设计从重规划初始点到入轨点的飞行弹道。根据目标轨道约束和火箭运行规律,结合最优控制原理设计火箭多级点火的弹道规划算法[4-5]。采用级数设计[6]与非线性规划[7-8]等方法进行问题求解,能够有效应对各种偏差,实现飞行弹道的快速规划。本文采用基于决策更新的弹道重规划方法完成任务决策,当存在飞行异常或偏差时能够根据任务要求,重新规划出一条满足条件的飞行弹道,尽可能保证任务顺利完成。即使偏差较大不能进入目标轨道,也要尽可能保证载荷进入次优轨道。
1 模型建立
在地心惯性坐标系OE-XEYEZE中描述火箭的质心运动方程,原点OE位于地球质心,OEXE在地球赤道平面内指向发射点所在经度线,OEXEYE平面为赤道平面,OEZE为地球自转轴,指向北极。
假设火箭发动机推力方向始终沿着体轴方向,并忽略附加哥氏力。考虑空气动力影响的条件下,根据牛顿第二定律,火箭在地心惯性坐标系中的运动方程如下
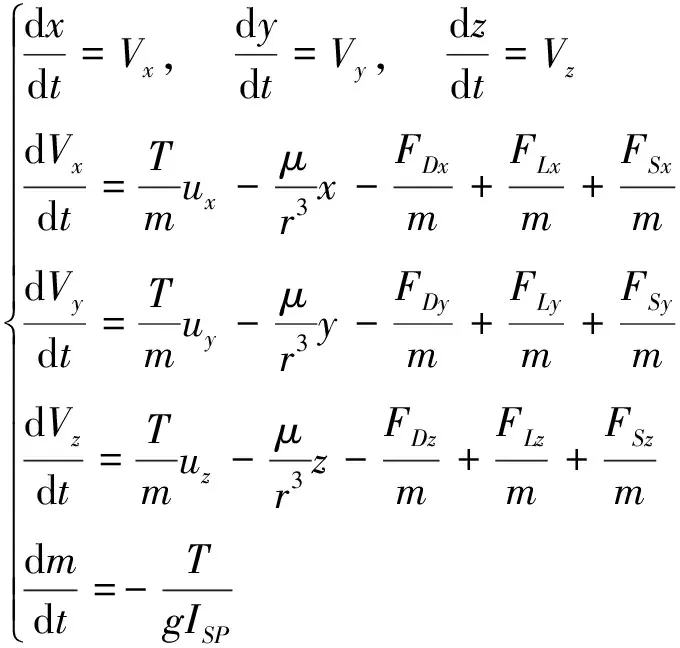
(1)
其中,r=[x,y,z]T为位移矢量在地心惯性系中的投影;V=[Vx,Vy,Vz]T为速度矢量在地心惯性系中的投影;ux,uy,uz为推力单位矢量分量;FDx,FDy,FDz为阻力分量;FLx,FLy,FLz为升力分量;FSx,FSy,FSz为侧向力分量;m为火箭质量;μ为引力系数;T为发动机推力;ISP为发动机比冲。
气动力在地心惯性系中的分量可以表示为

(2)

(3)
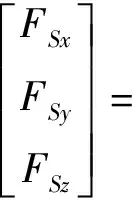
(4)
其中,ωE为地球自转角速度;L为发射点纬度;θ为弹道倾角;σ为航迹偏航角;A,B分别为
A=sinLcosθcosσ+cosLsinθ
B=sinLsinθcosσ-cosLcosθ
(5)
对于阻力,其数值可以表示为
(6)
其中,CD为阻力系数,由飞行马赫数和攻角确定;S为气动参考面积;ρ为大气密度;Vre为火箭相对于大气的速度。升力和侧向力的大小可同理求得。
多级火箭在上升段飞行过程中,各级的飞行状态有所不同。级间分离的过渡阶段需要满足约束[9]
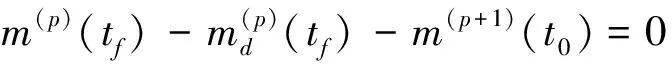
(7)
其中,p=1,2,…表示火箭不同的飞行阶段;md为级间分离抛去前级的质量。
多级火箭弹道重规划问题可以描述为最优控制问题,最优控制模型以有限推力作用下的质心运动模型(1)作为状态方程,系统包含7个状态量X=[x,y,z,Vx,Vy,Vz,m]T和3个控制量U=[ux,uy,uz]T。
初始状态为重规划起始点的位置、速度和质量,初始时刻状态由导航信息给定,即
X0=X|t=t0
(8)
目标集为满足终端约束要求的目标轨道根数,即
h(Xf)=0
(9)
当末端满足轨道根数半长轴a、偏心率e、轨道倾角i、升交点赤经Ω及近地点幅角ω五个终端约束时,具体可描述为[10]
(10)
其中,hN为目标轨道法向矢量,即
(11)
2 弹道重规划方案
2.1 轨迹规划
当运载火箭的飞行偏差在允许范围内,无需开展弹道重规划工作,采用系统自身的适应性调整就可以将载荷送入目标轨道。当超出总体给定的偏差,但超出偏差范围不大时,可以采用轨迹规划设计,综合考虑运载火箭实时位置、速度、目标及约束条件,通过快速规划算法得到满足飞行终端任务要求的弹道,将载荷送入目标轨道。
本文采用自适应伪谱法[11]实现运载火箭的轨迹规划设计,配点选择正交Legendre多项式的零点,积分过程采用Gauss积分公式。自适应伪谱法在传统伪谱法的基础上加入了自适应区间划分,在优化过程中可以更新配点设置,动态调整区间和函数阶次。这种方法可以更加灵活地完成优化问题的求解。
正交Legendre多项式的基点在(-1,1)之间取值,需要首先将时间变量[t0,tf]投影变换到[-1,1],即
(12)
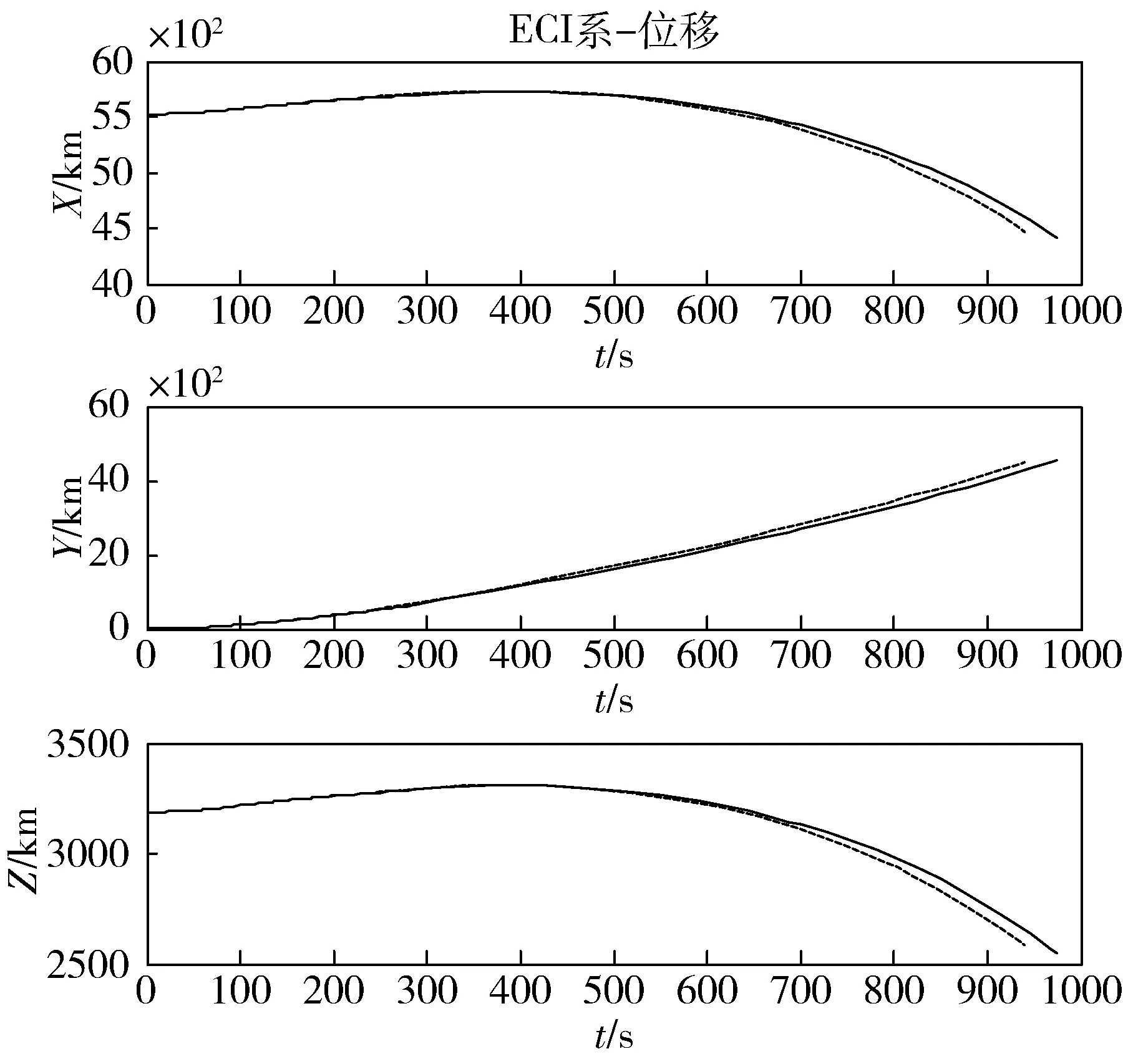
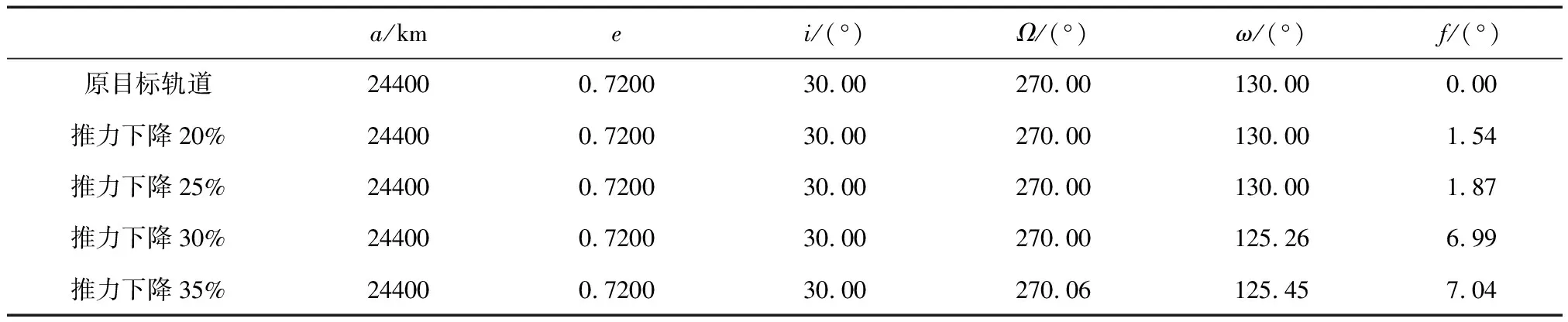
将连续最优控制问题转换为以基点处的状态变量和控制变量为未知系数的标准非线性规划问题,原来的连续问题转化成为离散问题。变量取值包括初值和K个基点值,时间变量有-1 (13) (14) (15) 性能指标可选取燃料消耗最少,对于推力大小不可调的火箭来说,等效于飞行时间最短。连续问题转化成为离散的最优问题,性能指标可以描述为 (16) 其中,Wk为Gauss积分公式中的积分权重,当基点数给定时为常值。 最优问题的约束条件包括地心惯性系中控制变量的单位化约束、变化率约束以及状态变量约束 (17) 其中,α表示控制变量变化率的幅值约束,将地球近似为圆球取半径RE。最优控制问题可以转化为非线性规划问题。对于非线性规划问题,可以采用SNOPT[12]求解器完成求解。 当运载火箭飞行超出的偏差范围过大,但尚未造成致命性故障时,载荷不能进入目标轨道。运载火箭需要开展弹道重规划工作,通过任务决策与轨迹规划将载荷送入次优轨道,对异常飞行状态实现一定程度的补救。为实现快速规划,可以先完成满足部分约束条件的规划任务,尽可能保证规划问题有解且收敛,之后通过提高约束条件和求解精度等方法更新任务决策,获得决策等级更高的高精度优化解。 如果无法将载荷送入预订目标轨道,需要规划出次优轨道或备用救援轨道。在飞行任务决策时,需要确定保留轨道根数的决策等级,提出合理可行的更新策略。保留轨道根数的决策依据主要包括任务需求、后续调整难度和可实现性等因素。综合上述因素,确定重规划方案保留轨道根数的决策等级。本文选用三级决策等级方案,如表1所示,其中“〇”表示需要满足约束条件的轨道根数,“—”表示不受约束允许出现偏差的轨道根数。表中等级III代表最低决策等级,等级I代表最高决策等级,任务决策等级越高,则终端约束条件越多,获得收敛解的难度就会越大。 表1 轨道根数约束的任务决策等级 任务决策等级的更新策略如图1所示。当火箭飞行过程中出现异常状态时,应急模式启动,开始弹道重规划任务。根据选用的决策等级方案,完成任务约束条件的初始化。本文不考虑导航系统故障,即认为系统提供的导航信息准确可靠,由导航信息可以确定初始时刻的位置和速度。根据火箭设计方案及燃油测量装置可以确定火箭的质量。位置、速度和质量信息共同构成优化问题的初始时刻状态量。建立优化问题,采用自适应伪谱法完成规划问题求解。在此过程中若是无法满足误差精度要求,可以更新配点设置后再进行规划求解。 图1 任务决策等级更新策略 由于火箭飞行的实时性要求,若在一定时间内无法得到确定的收敛解,需要对优化求解问题进行中断,满足中断条件即认为当前任务决策等级下无法快速获得收敛解。如果在最低决策等级条件下无法获得收敛解,则飞行偏差过大,即使通过弹道重规划也不能将载荷送入轨道。如果能够获得满足误差精度要求的收敛解,则对现有的火箭飞行弹道进行更新,并生成相应的制导指令。 为获得满足更多目标约束条件的飞行弹道,需要更新任务决策,增加约束条件以满足更高决策等级的要求。增加目标约束条件以后,原有的优化问题发生了变化,重新构建最优控制问题并进行求解。为提高迭代运算的收敛速度,可以采用之前决策等级条件下的弹道规划结果作为优化问题新的迭代初值。如果仍能获得满足误差精度要求的收敛解,则对飞行弹道和制导指令进行更新替换,同时继续更新决策等级,直到满足最高决策等级条件下的目标轨道约束要求。 为满足弹道规划的实时性要求,优化求解过程中配点数目不宜过多,这种条件下获得的弹道精度相对不高,制导指令可能存在一定的偏差。进一步更新配点设置,增加配点数量,可以获得更高精度的飞行弹道,生成更为准确的制导控制指令,从而完成火箭的自主弹道重规划。 以多级运载火箭上升段飞行为例,应用MATLAB对弹道重规划方案进行仿真验证。首先根据任务要求规划标称弹道。标称弹道可以直接采用本文提到的自适应伪谱法完成设计。 当火箭飞行过程中出现推力偏差和跟踪偏差时,采用本文所设计的任务决策方案,确定任务目标轨道根数的约束条件,并规划新的飞行弹道。 仿真具体参数如下: 运载火箭的初始位置在地心惯性系下分量:X=5.5236×106m,Y=0m,Z=3.1891×106m; 运载火箭的初始速度在地心惯性系下分量:Vx=0m/s,Vy=402.79m/s,Vz=0m/s; 对于多级火箭,载荷质量为4000kg,各级质量及推力参数如表2所示。 表2 多级火箭质量与推力参数 原有任务的目标轨道根数为:a=24400km,e=0.72,i=30°,Ω=270°,ω=130°,真近点角f=0°。火箭点火起飞后,正常情况下会按照预先设计好的标称弹道飞行。 本文选取t=150s作为异常状况发生点,此时也是弹道重规划的任务起始点。根据表2的有关参数可知,当t=150s时,运载火箭已完成助推级分离,正处于芯一级工作阶段。之后的过程包括芯一级剩余工作阶段、一二级分离、芯二级工作阶段。选择芯一级推力下降20%、25%、30%和35%这4种推力偏差情况,假设推力偏差情况下发动机比冲不变,剩余燃料仍能充分燃烧,级间正常分离并且芯二级能够完全正常工作。采用基于决策更新的方法完成弹道的重规划设计。 当推力下降20%时,重规划弹道与原标称弹道的位移、速度、控制变量对比如图2~4所示,其中虚线为原标称弹道变化情况,实线为重规划弹道变化情况。 图2 弹道位移对比 图3 弹道速度对比 图4 弹道控制变量对比 通过仿真过程可以验证,当推力下降20%时,任务决策等级可到达最高的I级,即半长轴、偏心率、轨道倾角、升交点赤经、近地点幅角5个终端约束均能满足原有要求。根据图2~4所示的仿真结果可以看出,推力下降时完成目标的飞行用时有所增加。 采用同样的方案可以确定推力下降25%、30%和35%情况下的重规划弹道。表3为原目标轨道、推力下降20%、下降25%、下降30%及推力下降35%重规划的目标轨道根数。 由表3可以看出,推力下降25%时,任务决策等级仍能到达I级,5个终端约束均能满足原有要求;推力下降30%时,任务决策等级可到达II级,目标轨道可以满足半长轴、偏心率、轨道倾角及升交点赤经4个终端约束条件;推力下降35%时,任务决策等级仅能到达III级,目标轨道可以满足半长轴、偏心率及轨道倾角3个终端约束条件。随着推力偏差的增加,弹道重规划任务可实现的决策等级会降低,能够满足的终端约束条件也随之减少。若进一步增大推力偏差,最低任务决策等级也有可能无法达到。 表3 不同推力偏差条件下的目标轨道根数 针对多级火箭上升段飞行的偏差问题,提出了一种基于任务决策等级更新的火箭弹道重规划方案。将多级火箭弹道重规划问题转化为最优控制问题,在考虑气动力和飞行约束的条件下,构造了火箭飞行的质心运动模型和最优控制模型。根据不同任务的特点设计任务决策等级方案,确定重规划任务的终端约束条件。采用自适应伪谱法快速生成高精度的收敛弹道,设计了当火箭飞行过程中出现推力偏差状况时的弹道重规划方案。仿真结果表明本文提出的方案能够快速规划出满足任务要求的飞行弹道,在火箭飞行出现异常状态时实现了一定程度的补救挽回。


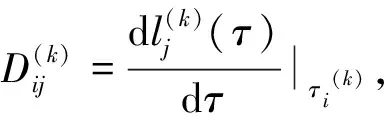
2.2 决策等级更新


3 仿真分析



4 结论

