机电伺服系统重复学习控制器设计

邸彩芸 乔 森 杨梦丽

1.国网冀北电力有限公司技能培训中心，保定 071051 2.保定电力职业技术学院，保定 071051 3.北京精密机电控制设备研究所，北京 100017 4.国网河南省电力公司检修公司，郑州 450000

在单片机、数字集成电路、稀土永磁电机和功率器件等电力电子技术飞速发展的技术背景下，近年来国内外机电伺服及其控制技术的发展十分迅猛。本文首先介绍了一种机电伺服系统原理，然后针对传统PID控制器的高速高精性能不足，设计了一种新型的重复学习控制器P+A-Type ILC，并在中大型柔性喷管负载条件下进行了试验验证。试验结果表明，本文的重复学习控制器P+A-Type ILC机电伺服技术方案满足型号高系统控制性能的特定需求，具有技术先进性。

1 机电伺服系统原理

本系统组成结构图如图1所示，本系统由1台机电伺服控制驱动器、1台机电作动器、1台动力电源和1套伺服电缆网组成。 机电伺服控制驱动器主要由控制电路模块和以IPM模块为核心的驱动电路模块2大部分组成。控制模块选用TI公司最新一代电机控制专用DSP处理器TMS320F28335，驱动模块选用Mitsubishi公司PM150RL1B060，逻辑控制芯片选用Lattice公司CPLD，外部数据存储器选用256K×16的SRAM，另外辅以电流、电压、速度检测和PWM 驱动等功能电路。

图1 机电伺服系统组成结构图

驱动电路模块采用交-直-交电压型主回路拓扑结构，为交流伺服电动机提供功率驱动，它包括电源电路、驱动电路、逆变电路和保护电路，且控制电源和驱动电源分别独立供电，驱动电源使用继电器进行软启动。采用光耦对PWM驱动信号进行强弱电隔离。

配套伺服电机则采用高比功率设计的3kW中频永磁同步电机。配套机电作动器采用直线一体式传动机构方案，具有结构紧凑、传动简洁、传动间隙小和装配调试简单等特点。机电作动器主要由永磁同步伺服电机、旋转变压器、滚珠丝杠、线位移传感器以及前后连接支耳等组成[1]。

快速、无超调和高精度是机电伺服系统的重要技术指标，同时满足这3项指标, 传统的设计方法已很难达到要求。根据国外的情况, 这类系统多采用智能控制技术。智能控制技术是将控制过程分成不同模态，在系统运行的不同阶段，选用合适的控制律，组合简单的控制方法实现高品质控制[2]。本文针对传统PID控制器的高速高精性能的不足设计了一种新型的重复学习控制器P+A-Type ILC。

2 重复学习控制器

重复学习控制算法(ILC)最早由m.uchiama 在1978年发表的文章中提出,其思想是利用上一个周期的运动结果，调整这个周期的控制量，以获得期望的性能。到目前为止，ILC一般有3种基本形式：P-type，D-type和A-type。重复学习算法比较重要的2点是：1)学习对的因果关系；2)学习算法的噪音水平。A-Type ILC的噪音水平很低，但其学习对不具有因果关系；而D-Type ILC学习对虽具有因果关系，但噪音水平很高。为了得到性能优越的重复学习算法，必须兼顾以上2点。由于系统的输出导数信息很难测量，且无论从测量或数据差分得到的值都会有很强的噪音，因此应尽量使用输出信息进行学习。故本项目采用p+A-Type ILC[3-4]。

在本文中，将机电伺服机构和速度环一起作为控制对象，这样机电伺服系统包括速度环控制器和位置环控制器。本机电伺服控制技术采用经典的基于转子磁场定向的矢量控制技术。控制器中速度环控制器和电流环控制器采用通用的PI控制器。位置环采用p+A-Type ILC控制器，从机电伺服速度给定ω(t)(位置环控制器的输出)到角位移输出θ(t)的传递函数为：

(1)

上式也即是p+A-Type ILC的控制模型[5-6]。

p+A-Type ILC的表达式如下：

ui+1(t)=ui(t)+k(oxd(t+Δ)-oxi(t+Δ))

(2)

由上述公式得出ui(t)对t时刻以后的系统输出有影响，因此可以使用t时刻以后的系统输出学习下一周的输入ui(t+1) ，这就是A-Type ILC的核心思想[7]。式中Δ是正常数，οxd(t+Δ)-οxi(t+Δ) 代表t+Δ 时刻系统跟踪期望运动的误差，A-Type ILC的学习对为(ui(t),oxi(t+Δ))，其因果关系可用下列表达式表述。

(3)

可见ui(t)在οxi(t+Δ)显示地出现，从而学习对具有因果关系[8]。

本文采用p+A-Type ILC位置控制器。其中，A-Type ILC用于机电伺服机构喷管惯量和有规律干扰诸如喷管和传动系统的补偿，而p控制器用于随机干扰的抑制。p+A-Type ILC控制模型在状态空间中可表达为[9]：

(4)

式中：ω(t)为机电伺服速度给定；θ(t)为机电伺服位移输出

x∈Rn；A∈Rn*n；B∈Rn*1；C∈R1*n；ω∈R。

由系统模型可知系统模型相对阶数为2。A，B和C的表达方式不唯一，本项目中选择如下的值

C=[1, 0, 0]

(5)

上述参数值满足：

(6)

控制目标就是使得机电伺服系统输出重复位移θi(t)来重复跟踪期望轨迹θ*(t)。θ*(t)为位置角度指令。定义轨迹跟踪误差

e(t)=θ*(t)-θi(t)

(7)

为第i周期时刻的轨迹跟踪误差。其中位移θi(t)为第i周期t时刻控制系统的位移输出[10]。

针对上述控制目标,则机电伺服系统p+A-Type ILC位置控制器设计如下：

(8)

p+A-Type ILC位置控制器的整个软件流程图如图3所示。

3 试验验证

试验验证重点考察在突加与突卸力矩负载时，位置环定位保持调节过程的动态能力，也就是位置环抵御高频扰动的能力，并与经典P位置控制器对比试验验证。试验系统平台采用完全具有自主知识产权的基于DSP TMS320F28335的10kW伺服驱动器，配套伺服电机则采用高比功率设计的3kW中频永磁同步电机，试验系统实物如图4所示[13]。

由上位机编程设定位置指令信息，位置指令设定幅值为0°的恒值信号，同时伺服控制器实时反馈自己的电机电压、位移、电流及速度信号，通过位置指令信号和各自电机的电压、电流、位移及速度信号记录突加负载和突卸力矩负载时的动态调节过程，从而体现位置环抵御高频扰动的能力。

图2 p+A-Type ILC位置控制器控制框图

图3 p+A-Type ILC位置控制器软件流程图

图4 试验平台

由于配套伺服电机采用高比功率设计的3kW中频永磁同步电机，额定转矩为19N·m，故试验中突加和突卸力矩负载为额定转矩19N·m，动态响应过程与3个闭环控制参数有决定性影响，故调试各个控制器参数直至震荡，参数设置为位置比例增益PA3=15，速度比例增益PA4=200，速度积分增益PA5=500，速度控制积分时间常数10ms，伺服转矩过载能力设置为200%[1]。

突加力矩负载试验结果如图5所示，由突加力矩负载试验结果可知，传统P位置控制器突加转矩负载后最大位置超调最大值达到了58°，动态响应稳定时间为135ms，而本文设计的p+A-Type ILC位置控制器位置超调最大值仅为27°，动态响应稳定时间为84ms，超调降低了53.5%，动态响应稳定时间缩短了38%。

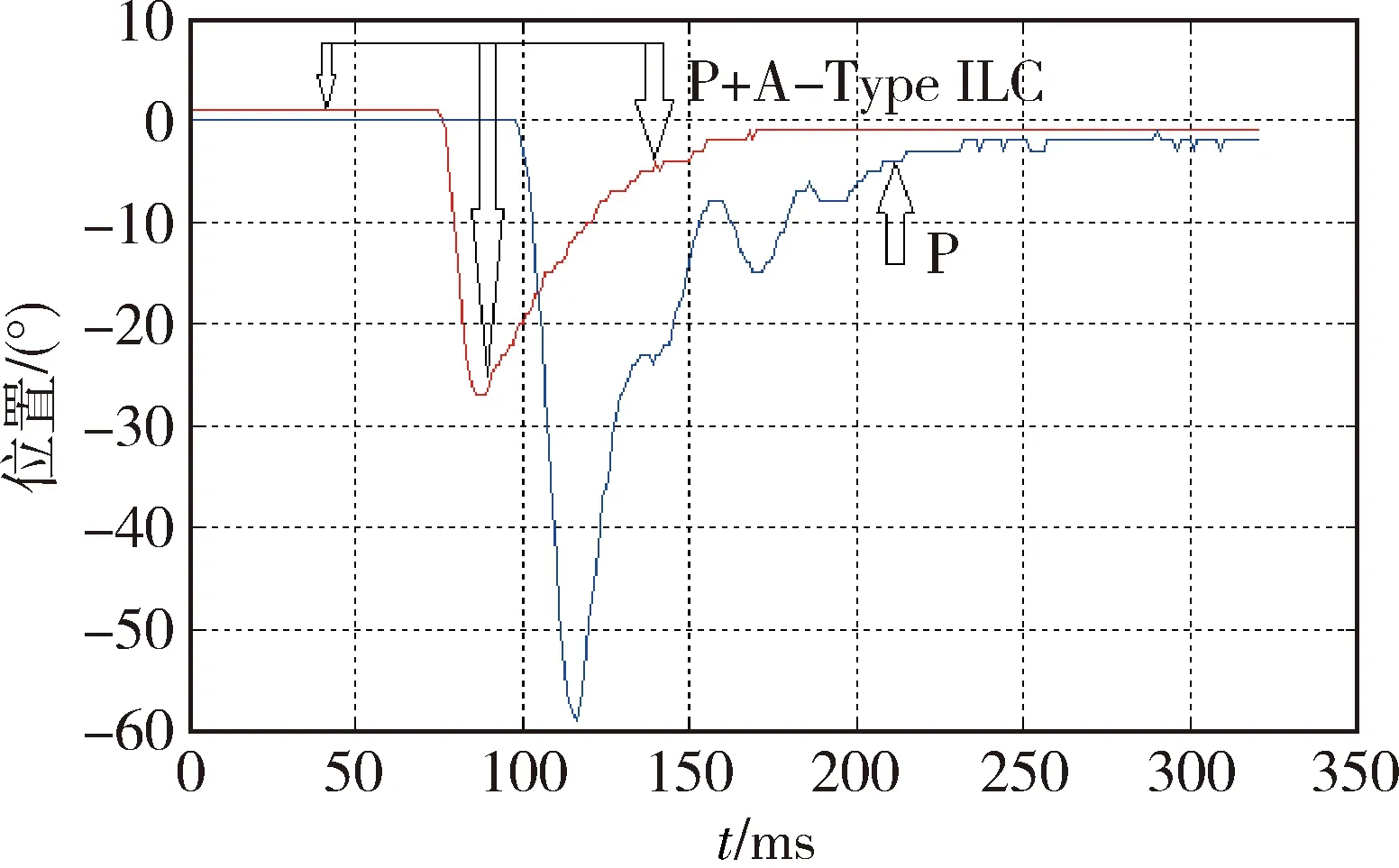
图5 突加19N·m转矩的位置调整过程

突卸力矩负载如图6所示。由突卸力矩负载试验结果可知，传统P位置控制器突加转矩负载后最大位置超调最大值达到了144°，动态响应稳定时间为82ms，而本文设计的p+A-Type ILC位置控制器位置超调最大值仅为65°，动态响应稳定时间为49ms，超调降低了54.8%，动态响应稳定时间缩短了41%，且传统P位置控制器在过渡过程中出现了严重振荡现象，显示在控制器策略中控制器的阻尼设计要比的p+A-Type ILC位置控制器差很多。

图6 突卸19Nm转矩的位置调整过程

4 结论

设计了一种p+A-Type ILC位置环重复学习控制器，速度环控制器和电流环控制器采用PI控制器，位置环采用p+A-Type ILC控制器，并进行了与经典P位置控制器的突加负载和突卸负载试验对比验证。突加负载试验表明，传统P位置控制器突加转矩负载后最大位置超调最大值达到了58°，动态响应稳定时间为135ms，而p+A-Type ILC位置控制器位置超调最大值仅为27°，动态响应稳定时间为84ms，超调降低了53.5%，动态响应稳定时间缩短了38%。突卸负载试验表明，传统P位置控制器突加转矩负载后最大位置超调最大值达到了144°，动态响应稳定时间为82ms，而p+A-Type ILC位置控制器位置超调最大值仅为65°，动态响应稳定时间为49ms，超调降低了54.8%，动态响应稳定时间缩短了41%，且传统P位置控制器在过渡过程中出现了严重振荡现象，显示在控制器策略中控制器的阻尼设计要比的p+A-Type ILC位置控制器差很多。p+A-Type ILC位置控制器实现了高速高精度的实时控制，满足了伺服系统时变非线性负载下的不同工况需求，系统鲁棒性大大提高。