未知纬度下基于四元数解算的SINS对准方法*
郑振宇 解维河 郑智林
海军大连舰艇学院,大连 116018
目前,基于惯性系的对准方法是捷联惯导系统(SINS)晃动基座对准的首选方案,其对准性能的优越性在船载、车载系统中均得到了充分的检验[1-4]。惯性系对准方法的本质为基于重力信息观测的矢量定姿算法,在构建参考矢量模型中需要精确的纬度信息支持,而在水下、地下、密林等无线电导航信号无法覆盖的环境下获得纬度信息并非易事。因此,未知纬度下SINS自对准方法研究成为近年来对准研究的一个重要方向。针对该问题,文献[5]提出利用重力矢量在惯性空间的角位置关系估计纬度,再利用估计纬度进行传统意义的惯性系对准,并分析了纬度估计的精度与对准精度。文献[6]提出了基于重力视运动的三矢量自对准方法,重新构造坐标系链式关系,将对准问题归结为利用矢量几何运算求解当前时刻导航系相对载体惯性系的姿态矩阵问题,为惯性系对准提供了一种新的思路。受其启发,本文将未知纬度对准问题转换为基于地球自转轴向矢量(简称地轴矢量)在参考坐标系下投影的求解问题,并提出了一种基于四元数的轴向解算方法,以此建立导航系轴向在惯性系下的正交投影,最后确定载体姿态关系,仿真实验与船载实验均验证了方法的有效性,并与传统方法进行了对比分析。
1 基于地轴矢量解算的对准思路
1.1 传统的惯性系对准思路

(1)
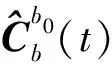
cosL=sin(θ/2)/sin(α/2)
α=ωie(t2-t1),cosθ=∠(gi(t1),gi(t2)
(2)

1.2 基于地轴矢量解算的对准思路

(3)

(4)
其中,×表示矢量叉乘,对各矢量单位化后可建立方向余弦矩阵:
(5)

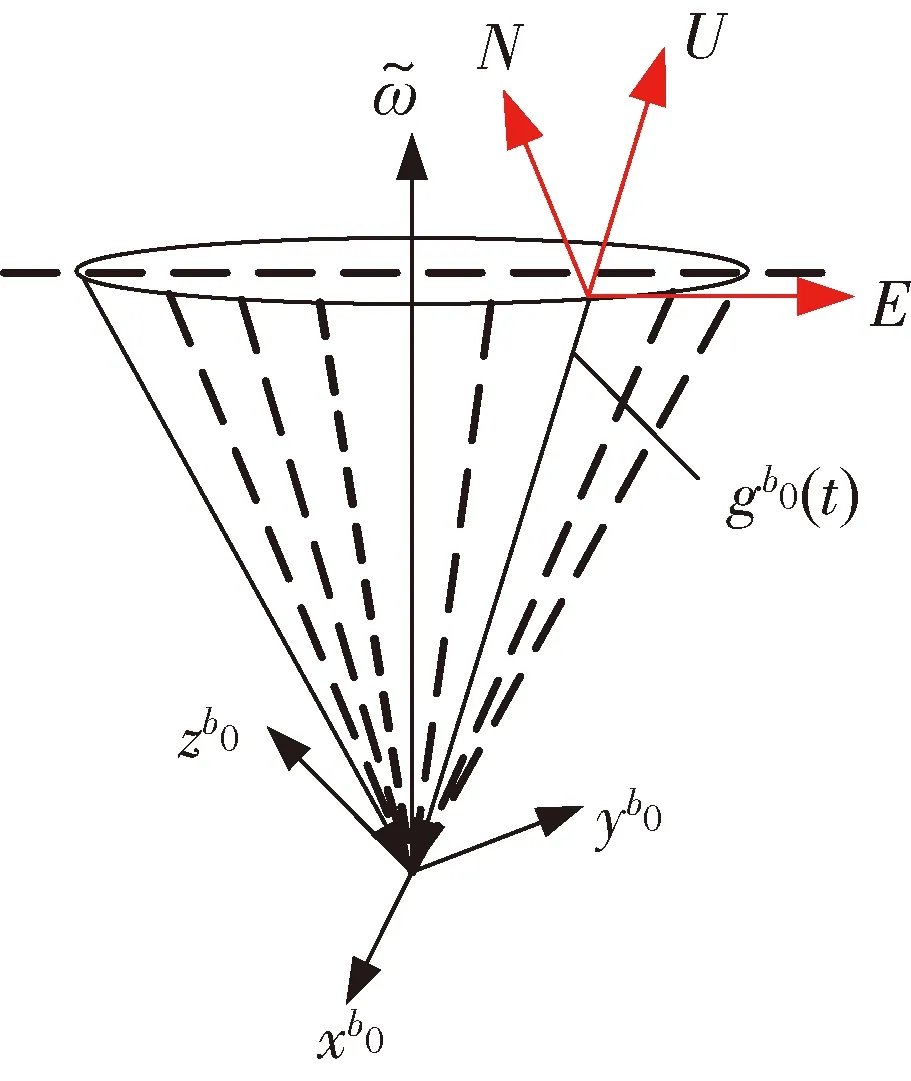
图1 重力矢量载体惯性系视运动
2 基于四元数解算的未知纬度对准方法
2.1 对准流程

(6)
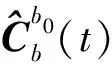
(7)

表1 低通滤波器参数设置
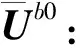
(8)

由正交关系可得:

图2 基于地轴矢量解算的惯性系对准流程
2.2 基于四元数的地轴矢量解算方法

(9)


(10)

(11)


(12)

(13)

(14)
3 仿真分析
仿真中设陀螺仪常值漂移为0.1(°)/h,随机漂移0.01(°)/h;加速度计零偏为1000μg,随机噪声为100μg。蒙特卡洛仿真次数设为100次,仿真步长设为0.01s。基座晃动航向ψ、纵摇θ及横摇γ角呈周期性变化,幅度分别为4°,5°与7°,摇摆周期分别为7s,5s与6s。设杆臂长度为(0.05m,0.05m,0.05m),横荡、纵荡和垂荡引起的线速度为呈周期性变化,其模型为:
Vd=Adωdcos(ωdt+φd)
(15)

对准解算分别采用先估计纬度再进行双矢量定姿惯性系对准解算的两步对准法与基于地轴矢量解算的对准方法。其中地轴矢量解算分别采用文献[6]的几何解析方法及本文的四元数解算方法。先不引入滤波环节,重点考查3种方法的对观测误差影响的鲁棒性,100次蒙特卡洛对准结果如图3所示,误差统计结果如表2所示。
图3 无滤波下准结果分布

图4 低通滤波下对准结果分布

表2 无滤波下各对准方法精度比较
由结果可看出,在没有施加任何滤波的情况下,3种对准方法精度相差较大。2步对准法水平对准精度要低于基于地轴矢量解算的水平对准精度,而基于地轴矢量解算的2种对准方法水平对准精度基本相当。在方位精度上,两步对准法与基于四元数地轴矢量解算的对准方法精度相当,后者略高于前者,而采用几何解析法进行地轴矢量解算的方位对准精度较差,究其原因是由于对准时间较短,解析中算法构建的中垂线方程易形成病态方程,矢量观测噪声过大时,易造成解算得到的轴向矢量误差过大甚至反向,算法在无滤波条件下可用性不强。综上,在无观测滤波的条件下,基于四元数地轴矢量解算的对准方法相对其它2种方法在精度上和算法稳定性上都表现出一定的优越性。
在前述仿真条件基础上引入表1参数的低通滤波环节,100次对准误差分布如图5所示,统计结果见表3。由结果可看出增加低通滤波环节后,各方法的对准精度都得到了一定提高,但各方法三轴对准精度以及不同精度表征参数的提高程度存在一定差异性,具体如下:
1)各方法的水平对准误差均值有所降低,相对而言,滤波后两步对准方法的水平对准精度较差。滤波后2步法水平对准误差均值降至20′以内,地轴矢量解算方法降至3′以内。代表精度稳定性的误差标准差参数滤波前后变化较大,2步法水平对准误差标准差由滤波前的3′以内降至0.2′以内,地轴矢量解算方法由滤波前的0.4′以内降至0.01′左右。
2)各方法方位对准误差滤波前后变化也比较明显,相对而言,滤波后基于四元数解算的对准方法的方位对准精度较高。其中,滤波后2步法方位对准误差均值由60′降低为8.39′,误差标准差由滤波前的58′降为3′;几何解析方法方位对准误差均值降低为60′以内,误差标准差由约196′降为6′以内;四元数解算方法误差均值由原来的30′降低为7′以内,误差标准差由约40′降为3′左右。

表3 低通滤波下对准方法精度比较
4 结论
本文将未知纬度下的晃动基座对准问题转换为基于重力矢量观测的惯性坐标系下地轴矢量解算问题,并提出了一种基于四元数的轴向矢量解算方法,通过仿真实验对比分析了其与传统的2步惯性系对准法及基于几何解析地轴解算对准法的精度特性。仿真表明基于四元数地轴矢量解算的对准方法相对其它2种方法在对准精度上和算法稳定性上表现出一定的优势,具有较强的工程应用性。

