问题导引 自然探究*
——苏教版五下《圆的认识》教学实录与思考
古希腊毕达哥拉斯学派认为,一切平面图形中最美的是圆形。从数学家的角度看,圆的美可能不仅指美学意义上的平衡、对称、和谐、圆满等,还在于圆较之其他图形蕴含着更为丰富的知识内容,涉及更多数学对象,对数学发展的作用更大。从小学数学教学的角度看,圆是小学阶段学习的第一个由曲线围成的图形,它对学生的发展价值有别于由直线围成的几何图形。所以,它是进行数学教学研究的一座富矿,许多数学教师都用它来展示自己的教学理念、教学主张。本节课以苏教版教材为依据,在借鉴既有研究成果的基础上确立自己的教学思路,即以问题导引,让学生自然地探究。
【教学过程】
一、引入
(课件出示苏教版五下第87页《你知道吗》栏目的图片。)
师:这些现象、物体和运动中隐藏着一种同样的图形,它是什么图形?
生:圆形。
师:今天,我们就一起来认识圆。(板书:圆的认识)
利用教材《你知道吗》栏目中的生活内容引入圆,简洁高效。
二、探究
1.画圆:探究圆的特征。
(1)在比较中初步认识圆
师:我们以前学过哪些平面图形?
生:长方形、正方形、三角形……
师:圆形与它们相比有什么相同和不同之处?
生:它们都是由线围成的图形。不同的是圆没有角,边是弯曲的;长方形、正方形都有角,边是直的。
师:说得真好!圆是由弯曲的线围成的图形。(在黑板上随手画一条弯曲线)这条曲线是不是我们随便画的弯曲线呢?
生:不是随便画的。
(2)自主画圆
师:你能画出一个圆吗?你打算怎样画?
(学生画圆,教师巡视。)
师:你是怎么画的?谁来介绍一下?
(学生有照着一个圆片描出来的,有拉线移动画的,有用圆规画的,有直接用手画的……教师选择随手画、照样子描、线栓笔画、圆规画四种情况展示。)
师:这几种方法你喜欢哪一种?为什么?
生:我喜欢照样子描,这样最简单,画得很标准。
师:这种画法有没有不好的地方?
生:它只能画这么大,不能任意改变大小。
师:有没有人喜欢别的方法?
生:我喜欢用圆规画圆,这样最方便、最标准,而且可以任意改变大小。
师:大家都这么认为吗?(生纷纷点头)哈,都是这样看,我也是这样认为的。圆规就是专门用来画圆的,用它可以标准、便捷、任意改变大小地画圆。有没有人喜欢这种用线拴着笔,然后移动笔画圆的?(生纷纷摇头)没有?大家为什么不喜欢?
生:太麻烦了,还要用手按着中间,而且稍微动一下就不标准了。
师:有道理!那这种方法有没有优点呢?
(教师点击课件,播放学生在操场上画大圆的视频。)
生:拉长线可以画比较大的圆。
师:看来每种方法都有优缺点。照样子描比较省事,但不能任意改变大小;用拉线的方法可以画比较大的圆,但没有圆规方便;用圆规画圆比较便捷而且标准,但不能画得很大;随手画的圆不标准,但省事,在画示意图的时候也可以用。所以,凡事要一分为二地看。
师:请大家说说,用圆规画圆时要注意什么?
生:要把圆规两脚分开,定好两脚间的距离。有针尖的脚要固定在一点上,旋转圆规时两脚间的距离不能变。
师:好,请大家按照刚才说的,用圆规在练习本上画一个圆。
(3)介绍圆规画法和圆心、半径、直径
师:老师也用圆规画了一个圆,请看,中心这个点叫什么?
生:圆心。
师:对,叫圆心,通常用字母O表示。关于圆,你还知道哪些名称?
生:我还知道半径和直径。
师:你能上来画一下吗?
(学生上黑板画,教师标注:半径r、直径d。)
师:仔细观察半径与直径,你能发现什么?
生1:圆心是直径的中点,直径两个端点都在圆上;半径一端是圆心,另一端在圆上;一个圆可以画很多条直径。
生2:直径长度是半径的2倍。
师:怎么证明?
生2:一条直径就是两条半径接起来的。
师:是的,一眼就看出来了。(板书:d=2r)还有别的发现吗?
生3:直径是圆上两点间最长的线段。
师:这是什么意思?你解释一下。
生3:就是在圆上不管你怎么画线段都不会比直径长。
师:这是真的吗?你怎么证明?
(学生上黑板,在圆上画线段,并解说:你可以随便测量一条线段的长度,它都没有直径长,最多和直径一样长。)
师:确实是这样。
(教师演示课件,解说图1。板书:直径是圆上两点间最长的线段。)

(图1)
师:大家还有什么发现?
生4:直径是圆的对称轴,沿着直径对折,两边能重合。
师:哈,你不仅发现直径是对称轴,而且给出了理由。真棒!(板书:对称轴)
师:你能用圆规画一个直径为5厘米的圆吗?请标出 O、r、d。
(展示点评学生所画的圆。)
通过与由直的线段围成的图形进行比较,凸显圆是由曲线围成的图形的特点。直边图形可以用直尺来画,那圆这个由曲线围成的图形怎么画呢?这个疑问自然地出现了,画圆的需要也就产生了。教师放手让学生用自己喜欢的方式画圆,然后分析各种方法的优缺点,帮助学生辩证地看待事物。利用学生既有的知识经验,引出半径和直径,通过聚焦圆的半径和直径来探究圆的特征。
2.套圆:深化理解特征。
(1)自主尝试在小圆外套画一个大圆
师:我这儿有个小圆,是照一个圆片描出来的,你能在它外面画一个大一点的圆正好把它套在正中间吗?
(学生独立解决,教师巡视,选择学生的作业(如图2)进行展示。)

(图2)
师:大家仔细观察,你觉得这位同学画的大圆正好把小圆套在正中间了吗?
生:有一点偏。
师:怎样才能将小圆套在正中间呢?小组讨论讨论。
(2)小组合作找圆心
师:哪个小组汇报?
生:我们组是这样做的,先画出一条直径,再量出它的长度是2厘米,半径就是1厘米,所以这就是圆心。
师:噢,原来他们是先找小圆的圆心,然后画的。大家同意他们的方法吗?都同意?我也同意。只要找到小圆的圆心就好办了。但是,你们怎么知道这条线段就是直径呢?
生:因为圆上最长的线段就是直径,我们试验了,它就是最长的。
师:哦,你们是用刚才找直径的方法找到的啊。其实,还有一种更快捷的方法来找直径。
(课件演示图 3,教师讲解。)
(图3)
师:找到小圆的圆心就容易画出外面的大圆了。两个圆的圆心相同,我们叫它们同心圆。
本环节继续深度认识圆的特征,这个行为不是直白地向学生提出要求,而是精心设计了一个类似游戏的任务——在未知圆心的小圆外套一个大圆来实现的。“套圆”任务等价于寻找圆心,等价于在圆上寻找直径,其实质就是直径是圆上最长的线段,长度是半径的2倍。“套圆”是包裹在圆知识外面的“糖衣”,使学生很想去品尝。
三、深化
1.画一个圆,让 A、B 两个点(如图4)都在圆上。学生独立尝试,教师巡视指导,学生汇报。

(图4)
师:还有不同的画法吗?(课件演示图5)这些圆都是经过这两个点的,这些圆的排列有什么规律?
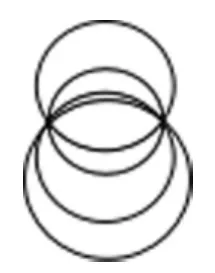
(图5)
2.在生活中,车轮为什么要做成圆形?
生:圆形的车轮容易滚动;滚起来比较平稳,不会上上下下的。
师:为什么圆形的车轮就比较平稳,不会上下颠簸呢?你能用所学的知识解释一下吗?
生:……
师(播放课件演示):我们在车轮上任意取A、B、C三个点(如图6),当车轮从A点着地滚到B点或C点着地时,车轮中心O点距地面的高度会不会变化?

(图6)
生:不会,高度一样?
师:为什么?
生:OA、OB和OC是相等的,因为它们都是圆的半径,圆的半径都相等。
师:是的。圆的半径都相等实际上就是说圆上的任意点到圆心的距离都相等,所以我国古代的数学家说:“圆,一中同长也。”
3.拓展:生活中的圆形物体非常多,如窨井盖、水管横截面等,你能用圆的一些知识来解释解释吗?课后大家可以去探索研究。
【教后反思】
1.理念:化陈述为探究。
数学知识总体上可以分为陈述性知识和程序性知识两大类,像“圆的认识”这类知识就属于前者,教材编排这类知识时往往采用陈述的方式,具体为:呈现生活中的相关事物→抽象出数学图形→介绍图形各部分名称→通过观察和操作活动认识特征→练习,强化理解。一些教师在教学这类知识时,往往习惯于按照教材的方式向学生进行知识的陈述,学生则进行有意义接受学习——了解是什么、理解为什么。其实,陈述性知识也可以进行探究式教学,让学生在主动观察、操作、猜想、尝试和验证的过程中发现它是什么、为什么是这样。就本节课教学而言,在学生经历观察圆、画圆、观察和发现直径、半径及其关系的过程后,又精心设计了“套圆”环节,使学生进行了兴趣盎然的探究学习。
2.实施:问题导引学生探究。
问题不仅能激发学生探究的兴趣,还导引着学生的探究行为。在引入环节,以“这些现象、物体和运动中隐藏着一种同样的图形,它是什么图形?”这一问题,让学生从日常生活中抽象出圆的概念和图形。探究环节设计了三个问题:圆形与由直的线段围成的图形相比有什么相同和不同之处?你打算怎样画?怎样才能画一个大圆将小圆套在正中间?第一个问题通过比较,让学生发现圆是由曲线围成的特征。第二个问题比较开放,让学生开动脑筋,个性化地画圆。对这些不同画法的比较分析,让学生认识到各种画法的优劣之处,有利于他们形成辩证的观念。同时,在进行这些操作和比较的过程中,已经向学生渗透了一些圆的知识,例如:圆的大小与圆规两脚之间的距离有关,与拉的线的长度有关;用手画圆时,铅笔尖应围绕着一个中心,尽量保持和中心相同的距离;等等。这些其实就是对半径、圆心等知识的感性认识。深化环节也有三个问题:第一个问题是在探究中不断深化学生对圆的知识的认识;第二个问题是让学生主动运用所学知识解释生活现象,这有助于发展学生在复杂的生活情境中运用知识的能力;第三题继续拓展学生的探究活动,让学生带着疑问走出课堂。

